Our work has been published in @Nature!!
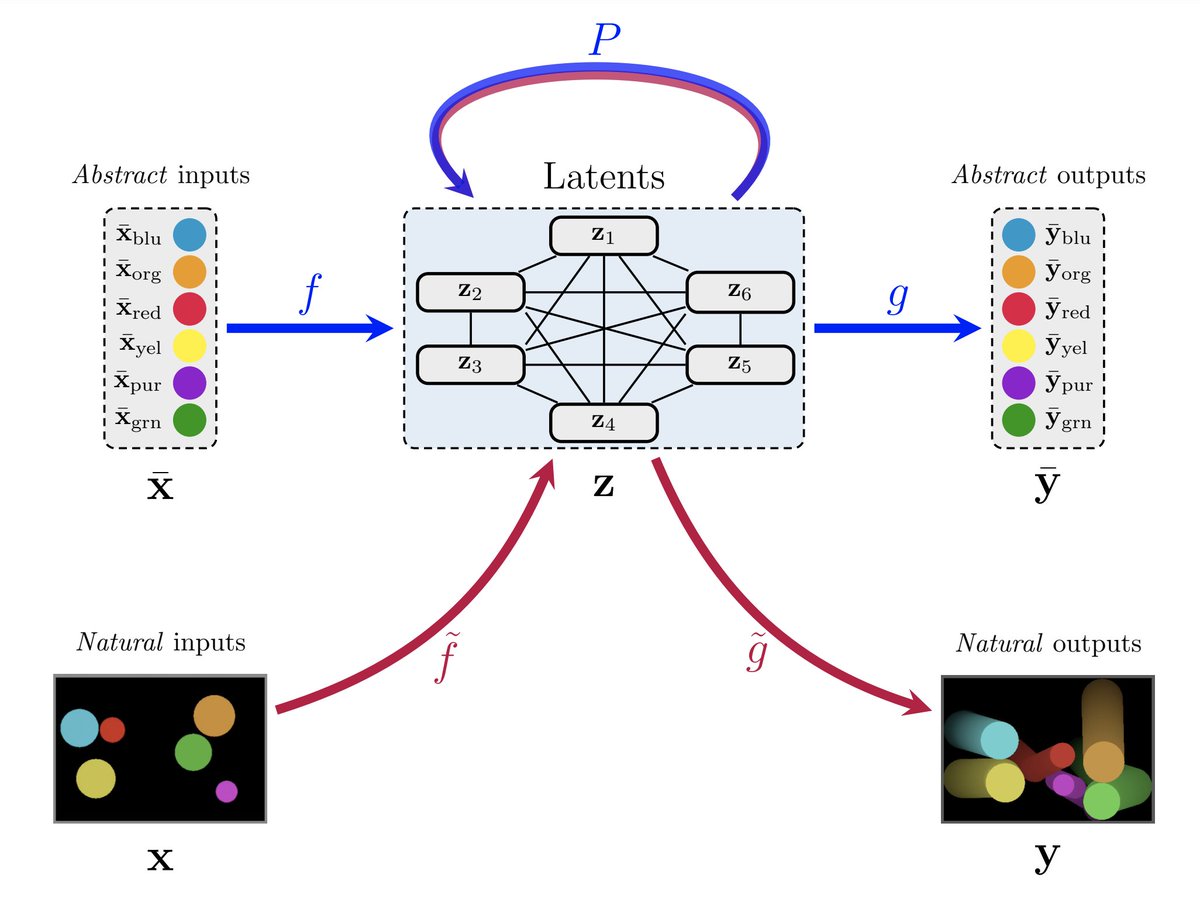
(G)NNs can successfully guide the intuition of mathematicians & yield top-tier results -- in both representation theory & knot theory.
dpmd.ai/nature-maths
arxiv.org/abs/2111.15161
arxiv.org/abs/2111.15323
See my 🧵 for more insight...
(G)NNs can successfully guide the intuition of mathematicians & yield top-tier results -- in both representation theory & knot theory.
dpmd.ai/nature-maths
arxiv.org/abs/2111.15161
arxiv.org/abs/2111.15323
See my 🧵 for more insight...
https://twitter.com/DeepMind/status/1466080533050535940
It’s hard to overstate how happy I am to finally see this come together, after years of careful progress towards our aim -- demonstrating that AI can be the mathematician’s 'pocket calculator of the 21st century'.
I hope you’ll enjoy it as much as I had fun working on it!
I hope you’ll enjoy it as much as I had fun working on it!

I was leading the GNN modelling on representation theory: working towards settling the combinatorial invariance conjecture, a long-standing open problem in the area.
My work earned me the co-credit of 'discovering math results', an honour I never expected to receive.
My work earned me the co-credit of 'discovering math results', an honour I never expected to receive.

We showed that combining algorithmically-inspired GNNs and rudimentary explainability techniques enables mathematicians to make meaningful progress on such challenging tasks.
AI is well-positioned to help as meaningful patterns emerge only once inputs get very unwieldy in size.
AI is well-positioned to help as meaningful patterns emerge only once inputs get very unwieldy in size.

To be clear: AI did _not_ discover the specific theorems and conjectures we expose here.
Mathematician experts did, _in synergy_ with predictions and interpretations derived from carefully-posed machine learning tasks. And this synergy is what makes the method so exciting, imho.

Mathematician experts did, _in synergy_ with predictions and interpretations derived from carefully-posed machine learning tasks. And this synergy is what makes the method so exciting, imho.


I’d like to deeply thank our collaborators: András Juhász, Marc Lackenby and Geordie Williamson. They successfully derived these results, put faith in our effort when we had no clear way to justify its promise, and remained a constant source of inspiration and encouragement.
Besides András, Marc & Geordie, our team comprised @ADaviesAI, Lars, Sam, Dan, @weballergy, Rich, @PeterWBattaglia @BlundellCharles @demishassabis @pushmeet
Thanks Alex, for asking me to join this effort during its formative stages and being a fantastic orchestrator throughout!
Thanks Alex, for asking me to join this effort during its formative stages and being a fantastic orchestrator throughout!
Last but not least: if you’d like to hear more about our work, I will be giving a keynote at the #AI4Science workshop @NeurIPSConf (ai4sciencecommunity.github.io).
Hope to see many of you there, and can’t wait to see the follow-up work that comes out of this!
Hope to see many of you there, and can’t wait to see the follow-up work that comes out of this!
• • •
Missing some Tweet in this thread? You can try to
force a refresh