Thread by @VisualAlgebra

I woke up a few days ago with the sobering realization: actually, I do NOT really understand groups actions.

Spoiler: I do now, but it took some work. And now I realize how incomplete my understanding was. 😳

Let me explain, I think some of you might enjoy this!

1/12 🧵👇

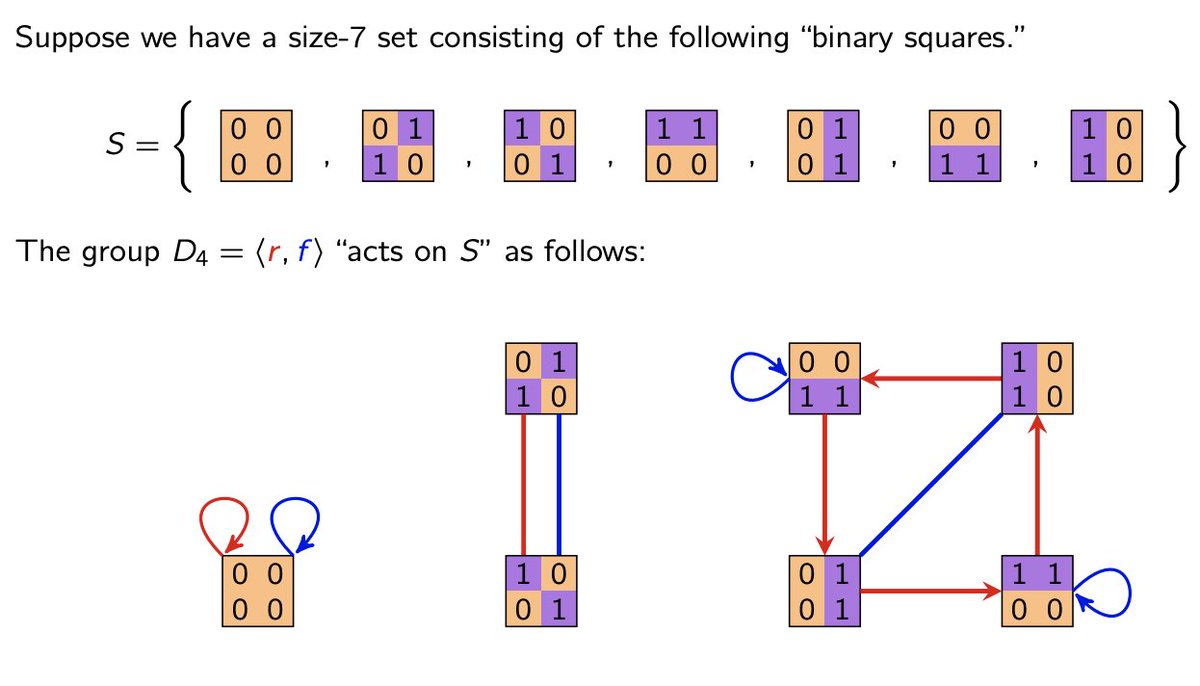
See those "orbit diagrams" above? I got to thinking: "how can we characterize all possible diagrams?" Equivalently, all transitive actions of D_4 (or a group G in general).

Playing around with things, I came up with a few more. But I still didn't know the answer. Do you?

2/12

For example, how many of the following are possible?

Before reading on, see if you can answer this, and generalize to arbitrary groups.

There's a simple elegant answer, that I was never aware of. And I suspect that the majority of people who teach algebra aren't either.

3/12

I was stumped, so I asked @chadgiusti, who is at the same conference as me, and who's teaching #VisualAlgebra this fall using these methods! 😍

It was fun to bat around some ideas, and I got new perspectives from him, but we still didn't have "clean answer."

4/12

But here's the key: in proving the orbit-stabilizer theorem, we exhibit a bijection between elements in the orbit, and (right) cosets of the stabilizer.

And stabilizers for elts in an orbit are conjugate.

I.e., each orbit corresponds to a conjugacy class of subgroups.

5/12

Now, the action of G on the (right) cosets of H can be realized in a (right) Cayley diagram by collapsing the *right* cosets of H.

In contrast, collapsing the *left* cosets results in the quotient G/H, but this only works if H is normal.

6/12

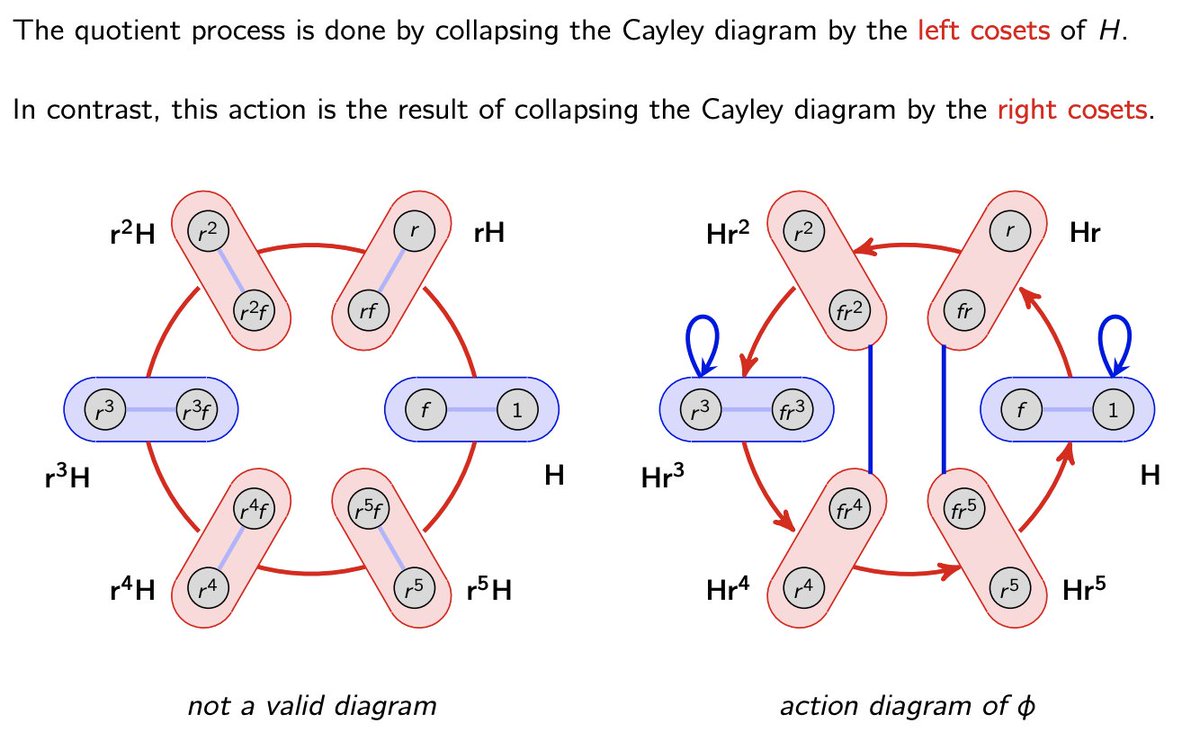
Do you see where I'm going with this? Could it possibly be that...every transitive group action (=1 orbit), is equivalent to...just collapsing by the right cosets of a group, namely the stabilizer???

Google, is this true??

OMG, I'm first aware of this...in my 40s?!?

🙀🤯

7/12

And that gives me a *fantastic* idea for a new visual! I made this one this evening by the pool in my South Florida hotel.

I now have an answer to my question in tweet #3 above, of which of those diagrams are possible.

8/12

My Chapter 4 is titled: "Maps Between Groups". This is basically "the theory of collapsing a diagram by LEFT cosets.

Chapter 5 is: "Group Actions". This is basically "the theory of collapsing a diagram by its RIGHT cosets". But only for normal subgroups.

9/12

And now I have new ideas for HW exercises! Here's the reduced subgroup lattice of D_6.

Exercise: construct the corresponding "lattice of transitive D_6 actions".

We've already seen one of them in this thread.

10/12

And next semester, I'm going to incorporate that into this HW problem, which you may remember from #Week10. Construct the action diagram, and find orbits, stabilizers, fixed points, etc.?

11/12

And that's my story of how I only came to finally "holistically understand" THIS WEEK what groups actions really are.

I love what @danaernst said when I texted him about it: "we don't know what we don't know!"

Anyone else realizing this for the first time today? 🙋‍♂️

12/12

CORRECTIOM: in tweet 9/12 above, I said “but only for normal subgroups”. That should have been in reference to taking a quotient (Ch 4 / collapsing left cosets) rather than Ch 5 / collapsing right cosets / defining an action.