Share this page!

Matt Macauley Profile picture
Twitter logo
May 28 • 23 tweets • 16 min read
Now that my #VisualAlgebra class is in the books, I want to post a long "meta thread" of all 16 weekly threads, with daily summaries. Here's my entire class, including lectures, HW, & exams, in one convenient place.

And stayed tuned for some surprise announcements below!👇🧵
We started #Week1 of #VisualAlgebra with a few quotes from "A Mathematician's Apology" on the beauty of mathematics, and then saw Cayley diagrams for the symmetries of the rectangle and triangle.

In #Week2 of #VisualAlgebra, we explored the Rubik's cube, more Cayley diagrams, group presentations, the impossibility of the word & halting problems, and we classified all frieze groups.

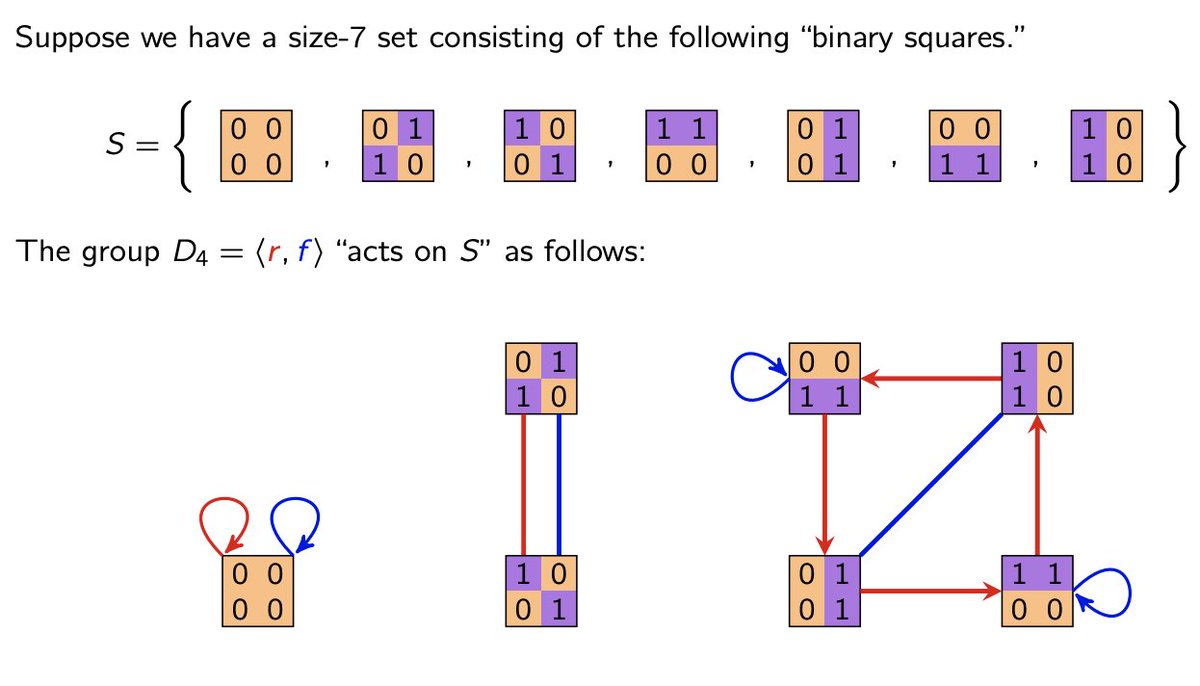
In #Week3 of #VisualAlgebra, we saw wallpaper & crystal groups, Cayley tables, quotients (informally). We saw some non-Cayley diagrams and tables (Latin squares), formalized the definition of a group, and saw cyclic & dihedral groups, and cycle diagrams.

In #Week4 of #VisualAlgebra, we classified finitely generated abelian groups, learned about permutations, and the symmetric & alternating groups, and saw many of their Cayley diagrams on beautifully laid out on Archimedean solids.

In #Week5 of #VisualAlgebra, we learned about some "uncommon" groups that we used throughout the semester: dicyclic, diquaternion, semidihedral, semiabelian. We also saw how to construct semidirect products of cyclic groups using Cayley diagrams.

We started #Week6 of #VisualAlgebra with groups of matrices, the Hamitonians, and a discussion of the classification of finite groups. Then we moved into subgroups & their lattices, cosets, and normal subgroups.

We started #Week7 of #VisualAlgebra with the tower law & normalizers. Then non-standard concepts: degree of normality, fully vs. moderately unnormal subgroups, and unicorns. Then conjugate subgroups and quotients, and well-definedness.

We started #Week8 of #VisualAlgebra with conjugacy classes of elements, and how "conjugacy preserves structure", and introduced "reduced subgroups lattices". We took a day off for #Midterm1.

We started #Week9 of #VisualAlgebra with conjugacy in S_n, and introduced the idea of "degree of centrality", and ended it with homomorphisms -- embedding & quotients, and finally, the fundamental homomorphism (1st isomorphism) theorem.

We covered the last 3 isomorphism theorems (correspondence, diamond, freshman) in #Week10 of #VisualAlgebra, then saw commutators, abelizations, automorphisms (inner and outer), and semidirect products.

We finished semidirect products in #Week11 of #VisualAlgebra. Then came group actions & "5 fundamental features: orbits, stabilizers, fixed point sets, kernel, global fixed points. We proved the orb-stab & orbit counting theorems & explored many examples.

We saw more examples of actions in #Week12 of #VisualAlgebra: groups acting on themselves, subgroups, & cosets. We used this to prove structure theorems. Actions of automorphisms, action equivalence, and we began Sylow theory.

What I did NOT do in #Week12 of #VisualAlgebra was to classify ALL transitive actions. I didn't actually realize how simple and elegant this was until after class ended. Next semester, I will include this material.

Bonus:
We finished Sylow theory in #Week13 of #VisualAlgebra, and saw how to show that there are no simple groups of order n, for certain n. Then we moved onto rings, saw LOTS of examples, and ended with ideals.

We began #Week14 of #VisualAlgebra with quotient rings, and then saw the isomorphism theorems. Then, maximal ideals, quotient fields, finite fields, and prime ideals. With #Midterm2 in the middle.

The last week of #VisualAlgebra lectures was #Week15: divisibility, factorization, & rings of algebraic integers. Primes, irreducibles, PIDs (and gcd & lcm), Euclidean domains, all that jazz. We finished with some open questions and some pretty pictures.

I guess finals week counts as #Week16 of #VisualAlgebra, and here's what our final exam looked like.



And now, as promised, onto some fun announcements! 👇

1/6
I'll teach #VisualAlgebra2 in #Spring2023, pending enrollment! And yes, I'll tweet daily summaries for that class too! Topics will include more ring theory, solvable & nilpotent groups, universal properties, free groups, presentations, field & Galois theory.

But FIRST....

2/6
I'll teach #GraduateVisualAlgebra in #Fall2022! Yes, our 1st semester grad algebra course can be visual. I'm not 100% sure how it'll go, but LOTS of basic proofs will be left as exercises (show __ is a subgroup, etc). And, I will be tweeting this course as well. Stay tuned!

3/6
I am finishing up my #VisualAlgebra textbook this summer, and I'm really excited how it's turning out! I will (eventually) be making all of my slides, including LaTeX files & images, freely available. For now, you can view my course materials here:

math.clemson.edu/~macaule/math4…

4/6
I'll be recording a brand new set of #VisualAlgebra #YouTube videos, covering basically my whole book (both semesters). Don't watch my old ones -- these will be MUCH better! And with professional audio equipment. (Shout out to @mathflipped for the help!)

5/6
Finally, as you can tell, I'm very passionate about these ideas, and love seeing others enjoy them. Please spread the word! On here or otherwise. If you're interested in teaching like this, I'm happy to share materials and/or meet over Zoom. Don't hesitate to get in touch!

6/6

• • •

Missing some Tweet in this thread? You can try to force a refresh
　

Keep Current with Matt Macauley

Matt Macauley Profile picture

Stay in touch and get notified when new unrolls are available from this author!

Read all threads

This Thread may be Removed Anytime!

PDF

Twitter may remove this content at anytime! Save it as PDF for later use!

Try unrolling a thread yourself!

how to unroll video
  1. Follow @ThreadReaderApp to mention us!

  2. From a Twitter thread mention us with a keyword "unroll"
@threadreaderapp unroll

Practice here first or read more on our help page!

More from @VisualAlgebra

Matt Macauley Profile picture
May 14
I woke up a few days ago with the sobering realization: actually, I do NOT really understand groups actions.

Spoiler: I do now, but it took some work. And now I realize how incomplete my understanding was. 😳

Let me explain, I think some of you might enjoy this!

1/12 🧵👇
See those "orbit diagrams" above? I got to thinking: "how can we characterize all possible diagrams?" Equivalently, all transitive actions of D_4 (or a group G in general).

Playing around with things, I came up with a few more. But I still didn't know the answer. Do you?

2/12
For example, how many of the following are possible?

Before reading on, see if you can answer this, and generalize to arbitrary groups.

There's a simple elegant answer, that I was never aware of. And I suspect that the majority of people who teach algebra aren't either.

3/12
Read 13 tweets
Matt Macauley Profile picture
Apr 27
Finishing up our🧵👇 #VisualAlgebra class in #Week15 with divisibility and factorization. I'm a little short on visuals, but here are two really nice ones on what we'll be covering, made by @linguanumerate.

Henceforth, we'll assume that R is an integral domain.

1/8 Mon ImageImage
The integers have nice properties that we usually take for granted:

--multiplication commutes
--there aren't zero divisors
--every nonzero number can be factored into primes
--any 2 nonzero numbers have a unique gcd and lcm
--the Euclidean algorithm can compute these

2/8 M
Some, but not all of these hold in general integral domains. This is what we'd like understand!

If b=ac, we say "a divides b", or "b is a multiple of a".

If a | b and b | a, they're "associates", written a~b.

HW: a~b iff they differ by a unit (i.e., a=bu).

3/8 M
Read 14 tweets
Matt Macauley Profile picture
Mar 29
We started #Week11 of #VisualAlgebra with a new diagram of one of the isomorphism theorems. I made this over spring break. The concept is due to Douglas Hofstadter (author of "Gödel, Escher, Bach"), who calls this a "pizza diagram".

1/14 Mon 🧵👇
Though we constructed semidirect products visually last week, we haven't yet seen the algebraic definition. On Friday, we saw inner automorphisms, which was the last step we needed.

Recall the analogy for A⋊B:
A = automorphism, B = "balloon".

2/14 M
Next, we asked when a group G is isomorphic to a direct product or semidirect product of its subgroups, N & H.

Here are two examples of groups that we are very familiar with.

3/14 M
Read 23 tweets
Matt Macauley Profile picture
Feb 23
We started #Week7 in #VisualAlgebra yesterday with the tower law.

Here are two ways to think about it. One involves cosets as "boxes" in a grid, and the other is in terms of the subgroup lattice: to find the index [H:K], just take the product of the edges b/w them.

1/8 Mon ImageImage
Pause for a quick comment about cosets in additive groups. Don't forget to write a+H, rather than aH. Here's a nice way to see the equality of a left coset and a right coset.

2/8 M ImageImage
Next, we proved that if [G:H]=2, then H is normal. Here's a "picture proof": one left (resp., right) coset is H, and the other is G-H.

3/8 M Image
Read 36 tweets
Matt Macauley Profile picture
Jan 20
WEEK 2 of #VisualAlgebra! This is only Lecture #2 of the class.

Monday was MLK Day, but on Wed, we learned about the Rubik's cube! I got to show up my rare signed cube with Ernő Rubik himself from 2010! Did a shout out to @cubes_art's amazing talents.

1/8 W ImageImage
We learned some neat facts about the Rubik's cube, like how the group has just 6 generators, but 4.3 x 10^{19} elements, and a Cayley diagram with diameter of 20 or 26, depending on whether you count a 180 degree twists as 1 or 2 moves.

2/8 W Image
I showed 3 different groups of order 8, and asked if any are isomorphic. At this point, all they know about what that means is that two groups must have identical Cayley diagrams *for some generating set*.

3/8 W ImageImageImage
Read 16 tweets
Matt Macauley Profile picture
Jan 14
WEEK 1: first lecture of #VisualAlgebra.

"The mathematician's patterns, like the painter's or the poet's must be beautiful; the ideas like the colours or the words, must fit together in a harmonious way."
― G.H. Hardy, A Mathematician's Apology

1/4
We have not yet defined a group. Rather, we are exploring the intuition of them via symmetries. This will *motivate the axioms*, rather than the other way around.

What properties does this group have what might not hold more generally?

2/4
For further insight, consider the symmetries of a triangle. This motivates the idea of relations, and why this "group calculator" tool is useful.

I got so many really good questions and comments in class today. How often does that happen on *Day 1* of abstract algebra??

3/4
Read 4 tweets

Did Thread Reader help you today?

Support us! We are indie developers!

This site is made by just two indie developers on a laptop doing marketing, support and development! Read more about the story.

Become a Premium Member ($3/month or $30/year) and get exclusive features!

Become Premium

Don't want to be a Premium member but still want to support us?

Make a small donation by buying us coffee ($5) or help with server cost ($10)

Donate via Paypal

Or Donate anonymously using crypto!

Ethereum

0xfe58350B80634f60Fa6Dc149a72b4DFbc17D341E copy

Bitcoin

3ATGMxNzCUFzxpMCHL5sWSt4DVtS8UqXpi copy

Thank you for your support!

Follow Us on Twitter!

:(