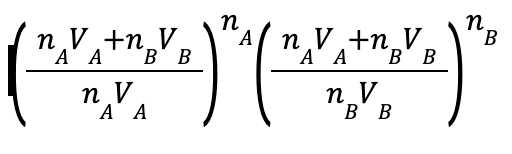Thread by @zhigangsuo

#thermofact
What does the Boltzmann constant mean?

1/ Temperature has many units, among which are Kelvin and Joule. The two units covert as

1 Kelvin = 1.380649 × 10^−23 Joule

This conversion factor is called the Boltzmann constant, k.

It is analogous to

1 inch = 2.54 cm

2/ It looks silly to name an unsightly conversion factor after three great names: Joule, Kelvin, and Boltzmann.

All units are silly, but they are necessary evils.

Let's learn about the two units of temperature, Kelvin and Joule.

3/ Entropy of an isolated system is defined as the logarithm of the number of quantum states of the isolated system:

S = log Ω

For a thermal system, which transfers energy with surroundings, entropy is a function of energy, S(U).

Temperature T is defined by

1/T = dS(U)/dU

4/ Inspect the two definitions:

S = log Ω
1/T = dS(U)/dU

We see that
-entropy is dimensionless
-temperature has the same dimension as energy, Joule.

5/ But Joule is a giant unit of temperature. Humans like to have a much smaller unit, Kelvin.

Kelvin had a convoluted historical definition. Since 2019, Kelvin has been defined by

1 Kelvin = 1.380649 × 10^−23 Joule

The value is set by a committee!
en.wikipedia.org/wiki/2019_rede…

6/ Nature is indifferent to how humans define a unit for temperature.

To state any fundamental relation of nature, if temperature T is in the unit of Kelvin, the product kT must appear together.

7/ When temperature is reported in Kelvin, to maintain the equation 1/T = dS(U)/dU, the entropy need be in the fake unit of k:

S = k log Ω

If we report entropy S in this fake unit, only the ratio S/k can enter any fundamental result.

Nature is indifferent to human’s units

8/ Thus, we clutter entropy with a fake unit Joule/Kelvin.

The concept of entropy is about the number of quantum states, which has nothing to do with either energy or temperature.

It takes time to explain k in

S = k log Ω

The fake idea has gone far.