Thread by @pgroisma

#TeRegaloUnTeorema se despierta del letargo para honrar al enorme Luis A. Caffarelli, que se alzó nada menos que con el Premio Abel 🙌

🆃🅴🅾🆁🅴🅼🅰 🅳🅴 🅲🅰🅵🅵🅰🆁🅴🅻🅻🅸
(y Kohn y Niremberg).

Las cosas no pueden ir demasiado mal con las ecuaciones de Navier-Stokes.
🧵

Desde que Newton y Leibniz nos enseñaron a derivar, hace ya más de 300 años, y Newton dijo F=m ·a, las ecuaciones diferenciales son la herramienta por excelencia para tratar de comprender nuestro mundo físico y resolver muchísimos otros problemas en ingeniería, economía...

..., biología,química, oceanografía, ciencias de la atmósfera, finanzas y la lista sigue…

No son la única, y de hecho el 𝘥𝘦𝘦𝘱 𝘭𝘦𝘢𝘳𝘯𝘪𝘯𝘨 es tal vez la primera competencia seria que apareció en estos más de 300 años (con las ventajas y serios problemas que eso trae, pero que no discutiremos hoy).

Otras herramientas son también muy importantes, pero las ecuaciones diferenciales tienen un lugar muy muy especial.

Sirven para describir desde la deformación del espacio-tiempo y el movimiento de los planetas hasta el estado de un sistema cuántico. En el medio, todo lo que puedan imaginarse: campos eléctricos y magnéticos, difusión de calor y otras cantidades, ...

... evolución del precio de activos financieros, dinámica de poblaciones (de bacterias, personas u otras especies), epidemias, propagación de ondas, evolución de la atmósfera terrestre y/o sus océanos… (sigo?)

Son ecuaciones como las que nos daban en la escuela en el sentido que estamos interesados en una incógnita x, que no sabemos cuánto vale pero que sí sabemos que verifica una relación (ecuación). Y entonces el objetivo es resolver la ecuación para poder ganar información sobre x.

En las ecuaciones de la escuela, x era un número y entonces nos conformábamos con conocer cuánto valía ese número. A eso le llamábamos resolver.

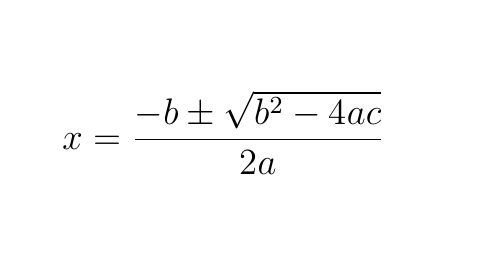
En las ecuaciones diferenciales la incógnita no es un número sino que es un objeto más complejo. Puede ser una función, o un conjunto de funciones, o una curva, o una superficie, o incluso cosas más complicadas.

Y en general no se puede “resolver” en el mismo sentido que resolvíamos las ecuaciones de la escuela, pero al cabo que ni queremos, porque aunque pudiéramos “resolver”, no ganaríamos mucho, más allá de saber que hay una solución (que igual no es poco, ya van a ver).

Entonces en general preferimos hacer dos cosas:

1. Usar el análisis matemático para describir propiedades de la solución usando el hecho de que sabemos que cumple la ecuación. Es decir, usando sólo el hecho de que hay un objeto que resuelve la ecuación, queremos deducir qué propiedades debe tener ese objeto.

2. Usar computadoras y algoritmos adecuados para calcular aproximadamente la solución de nuestra ecuación.

Las dos cosas se basan en un hecho fundamental: asumen que existe una solución. Y entonces el problema del millón (posta, ya verán), pasa a ser demostrar que existe una solución de la ecuación.

Las ecuaciones de Navier-Stokes, que datan de 1820, sirven para modelar el movimiento de un fluido incompresible (¿lo que?): agua, corrientes en los océanos, aire alrededor de una avión mientras vuela, la atmósfera terrestre.

Más vale que queremos conocer las soluciones de esas ecuaciones! Las necesitamos para entender cómo debe ser un avión para volar (confortablemente si se puede), para predecir el tiempo, entender las corrientes en los océanos y muchas cosas más.

Pero, ¿sabes qué? Al día de hoy no sabemos si siempre existe una solución de la ecuación.

Y hecho es posta el problema del millón, ya que el Clay Institute estableció en el año 2000 un premio de 1 millón de dólares para quien(es) demuestren que siempre existe una solución o que, por el contrario, demuestren que hay situaciones en que puede no existir una solución.

Y adivinen quienes fueron los que más se acercaron a resolver el problema? En 1982 Caffarelli, Kohn y Niremberg publicaron el artículo

... donde demostraron que las candidatas naturales para resolver la ecuación, las llamadas soluciones débiles, funcionan bastante bien.

No demostraron que resuelvan posta-posta la ecuación pero demostraron que si llegara a ser el caso que no la resuelven posta-posta, es por poquito. Tan poquito que podemos hacer de cuenta que sí las resuelven (con los recaudos necesarios).

¿Te preguntás entonces si es por esto que le dieron el Abel a Caffarelli?

Esto es solo una pequeña parte de su obra. Además es considerado uno de los máximos líderes mundiales en lo que hace a los problemas de frontera libre por su contribuciones fundamentales y por la escuela que creó...

Pasa algo similar con los problemas de homogeneización y las ecuaciones integro-diferenciales. Entre otras cosas.

Una vez más ¡Felicitaciones Luis!

#TeRegaloUnTeorema