Thread by @TamasGorbe

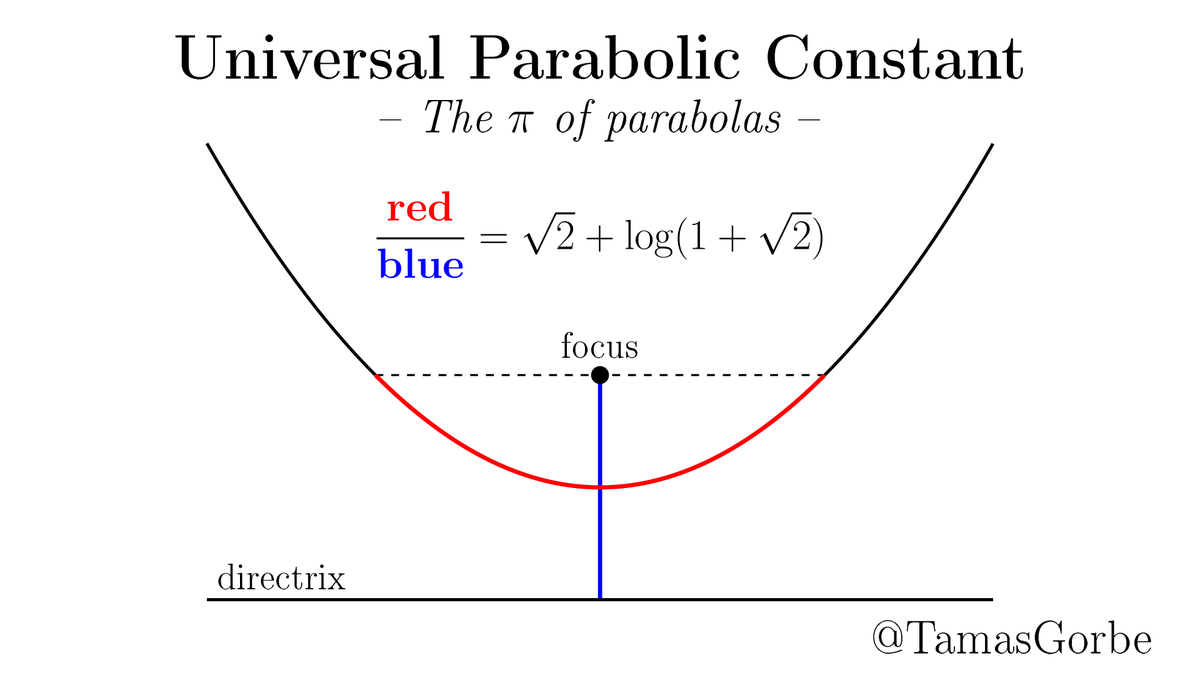
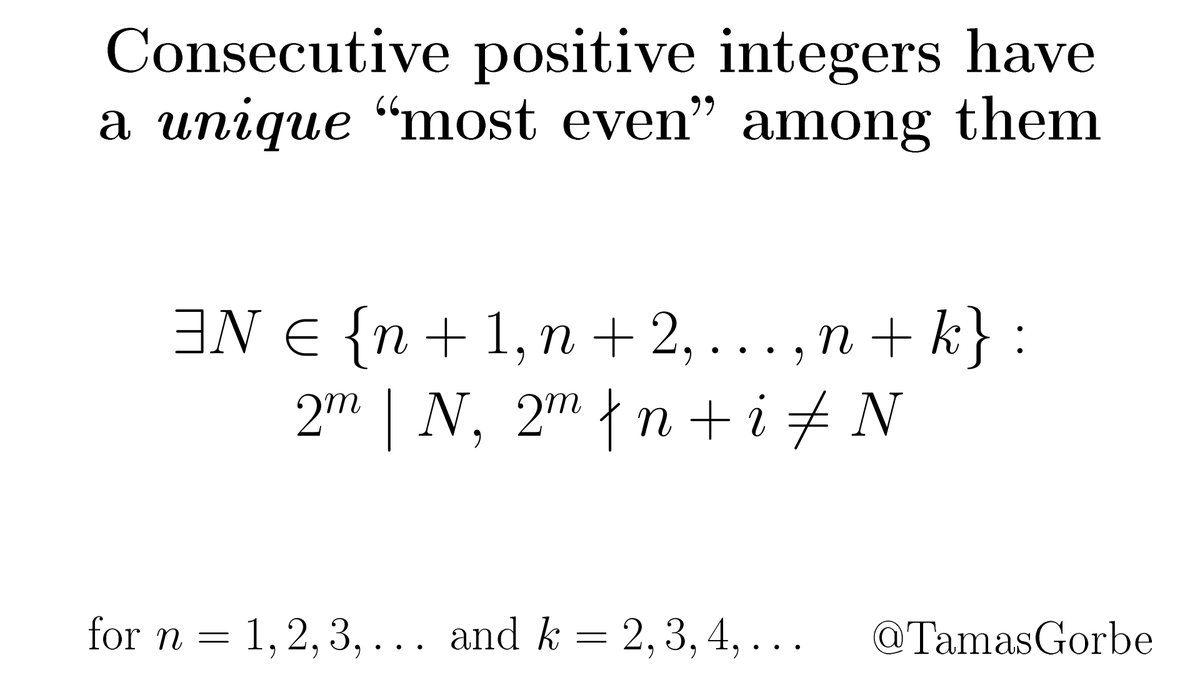If you trace a point on the circle rolling around another circle of equal radius you get a heart-shaped curve called the cardioid. ❤️ It has all sorts of cool properties. This week on #50FamousCurves we'll be circling around this beauty! 😀 [Wiki bit.ly/2GEL2Oy]

Fun fact about the cardioid: Its name comes from the Greek καρδία "heart". #50FamousCurves

How to draw a cardioid? You only need two cups, a pencil and a couple of rubber bands. #50FamousCurves

Fun fact about the cardioid: It appears in the Mandelbrot set. Namely, the boundary of the central bulb of the Mandelbrot set is a cardioid. #50FamousCurves

How to draw a cardioid?
1) Draw a circle.
2) Divide its perimeter into many equal arcs using N points labelled 1,2,...,N.
3) Draw the chords connecting point n to point 2n (take mod N if needed) for all n.
The envelope of these chords is a cardioid.

Fun fact about the cardioid: Many microphones have cardioid-shaped sensitivity patterns. This is very useful when you want to capture sound coming from a specific direction and reject sounds from other directions, e.g. vocal and speech microphones. #50FamousCurves

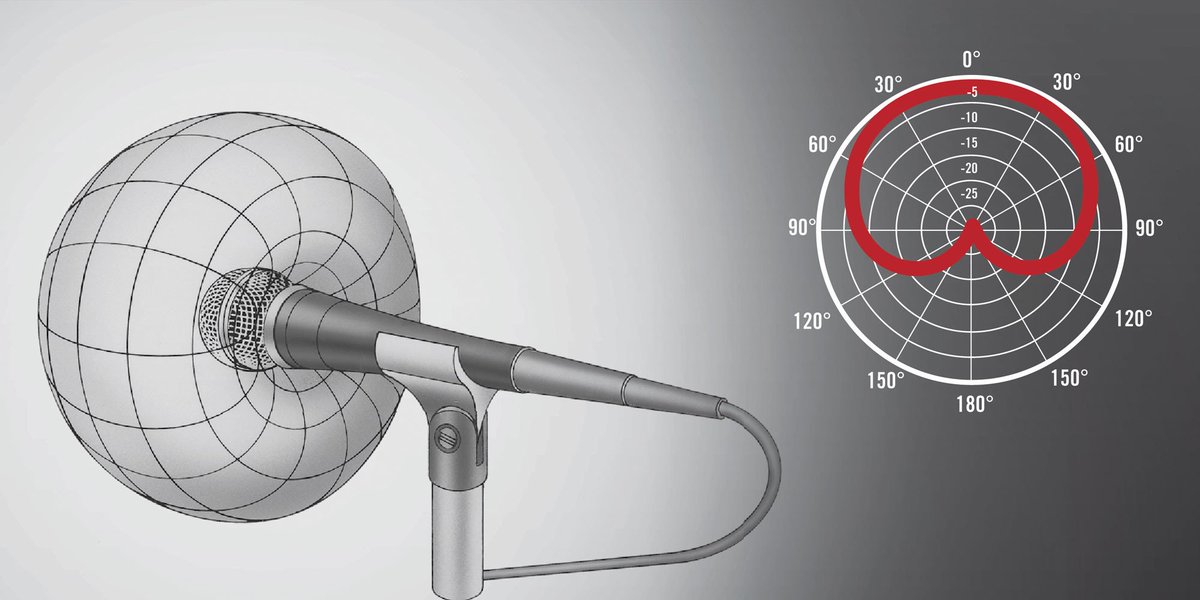
How to draw a cardioid?
1) Draw a circle.
2) Pick a point P on the circle.
3) Draw many tangents of the circle.
The foots of perpendiculars from point P on these tangents are points of a cardioid. #50FamousCurves

Fun fact about the cardioid: Cardioids are all around us. They appear when light bounces off the rim of a conical cup with the light source placed along a generatrix of the cone. It is because the rays reflected on a circle are tangents of a cardioid. #50FamousCurves

How to draw a cardioid?
1) Draw a circle.
2) Pick a point on the circle.
3) Shine light from this point.
The rays reflected on the perimeter are tangents of a cardioid. #50FamousCurves

How to draw a cardioid?
1) Draw a circle C.
2) Pick a point P on C.
3) Draw circles with their centres on C and passing through P.
The envelope of these circles is a cardioid. #50FamousCurves

How to draw a cardioid?
1) Draw a circle of radius r.
2) Fix a point P on the circle.
3) Connect P to a point Q≠P on the circle.
4) Let A,B denote the points on the line PQ such that |AQ|=2r=|QB|.
As Q goes around the circle A and B trace a cardioid. #50FamousCurves

How to draw a cardioid? 1) Take the unit sphere S: x²+y²+z²=1. 2) Draw the parabola P: y=x²-1/2 in the (x,y) plane. 3) Project P to S by shining light from the North Pole (0,0,1). 4) Turn the curve on S upside down. The rotated curve projects to a cardioid. #50FamousCurves

Here's a wonderful short film by Trevor Fletcher, produced by Association of Teachers of Mathematics @ATMMathematics. It illustrates most of the properties of the cardioid.

Fun fact about the cardioid: Circles always have 2 parallel tangents. Cardioids have 3. #50FamousCurves

I hope you enjoyed learning about the beautiful Cardioid curve this week. If you did, share this thread with your friends! 🙂 Of course, there's more to it than the things mentioned here, but we'll move on and have a new curve next week. #50FamousCurves