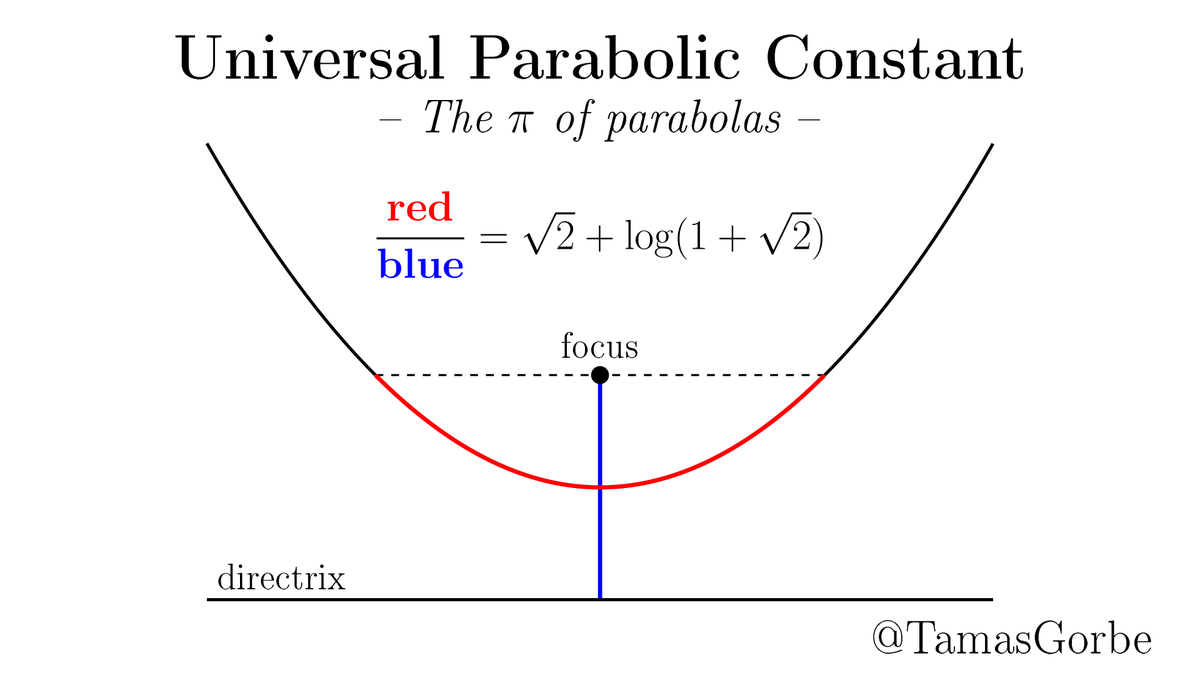
Proof. If P was algebraic, then so would P–√2 = log(1+√2) and by the Lindemann-Weierstrass theorem exp(P–√2) = 1+√2 would be transcendental, which it isn't.
What could the exact value be?
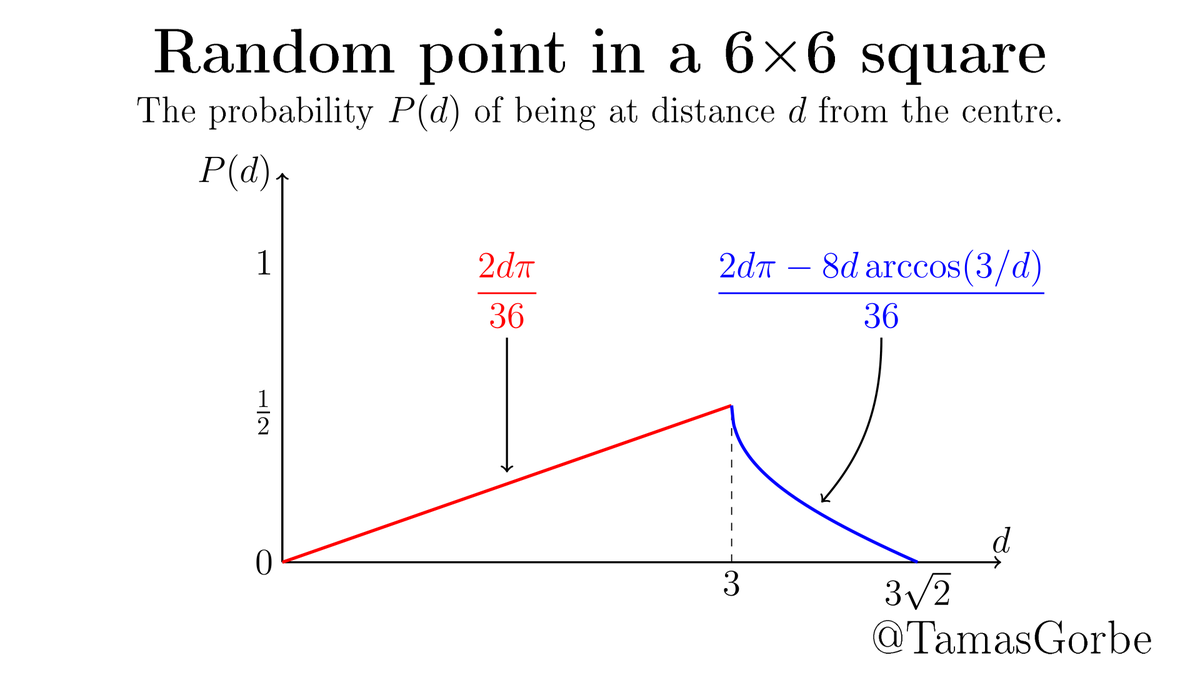
The probability of being at distance d from the centre is proportional to the length of arc(s) of radius d that's inside the square. To get probabilities, one needs to normalize by 36, the area of the square.
The results is, of course, the universal parabolic constant.