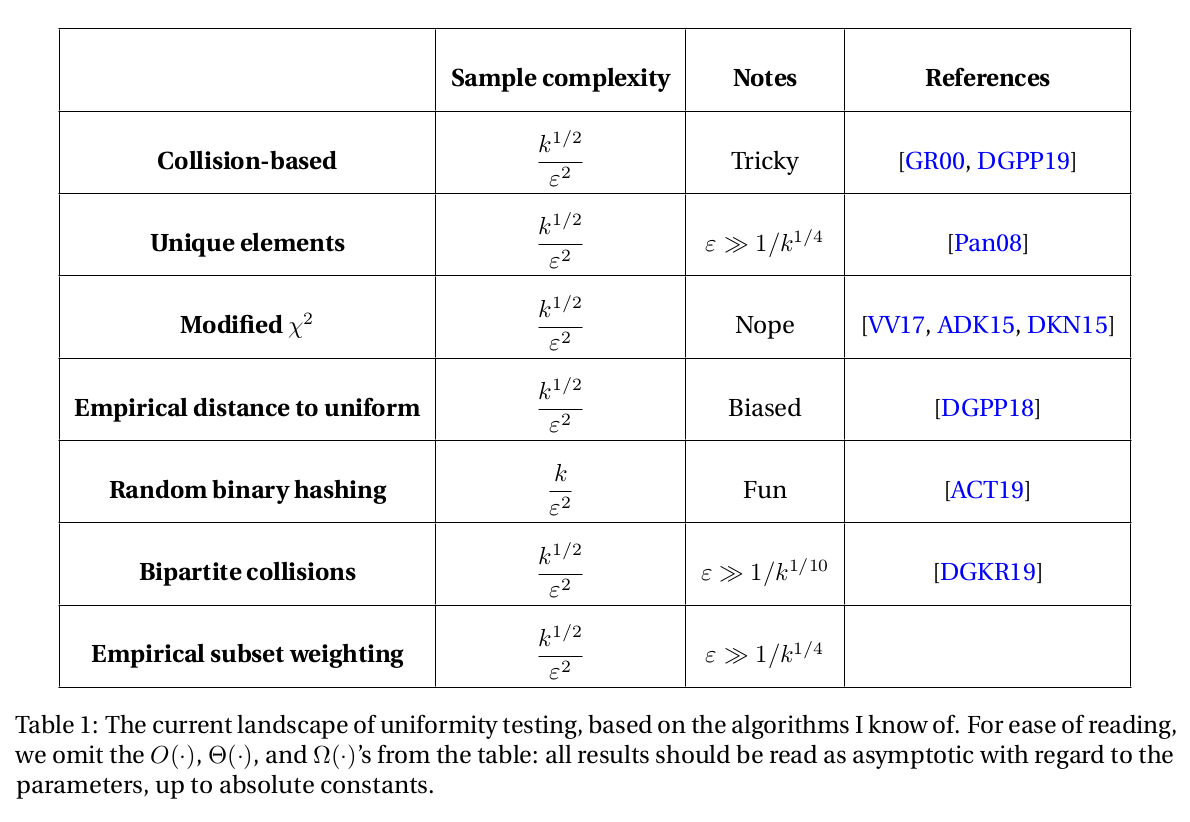
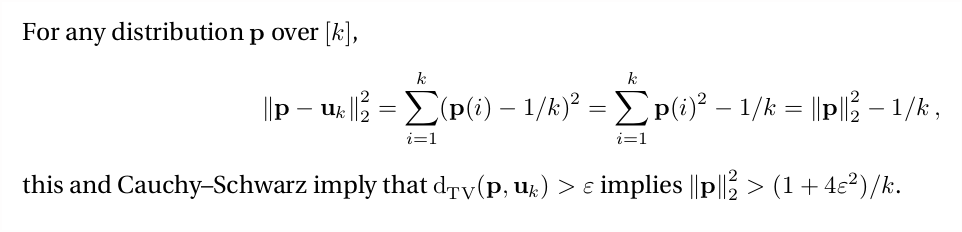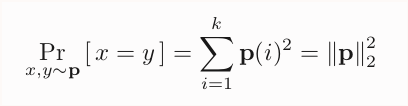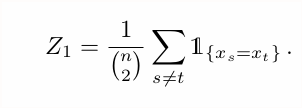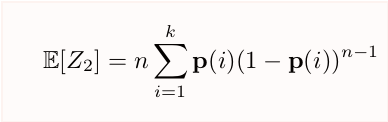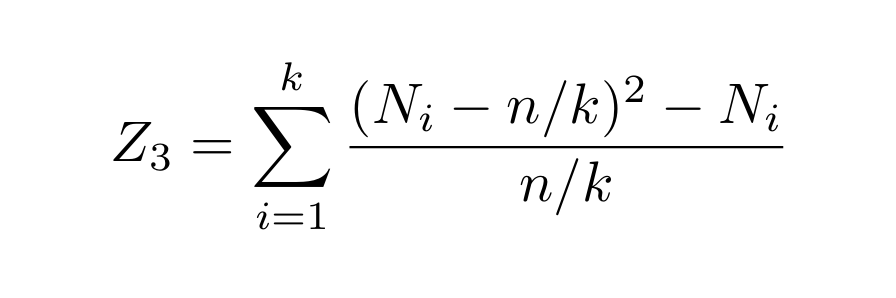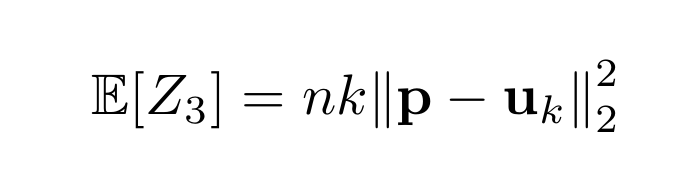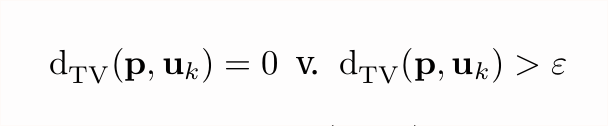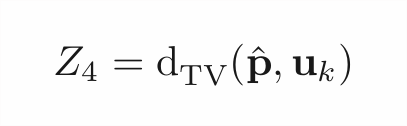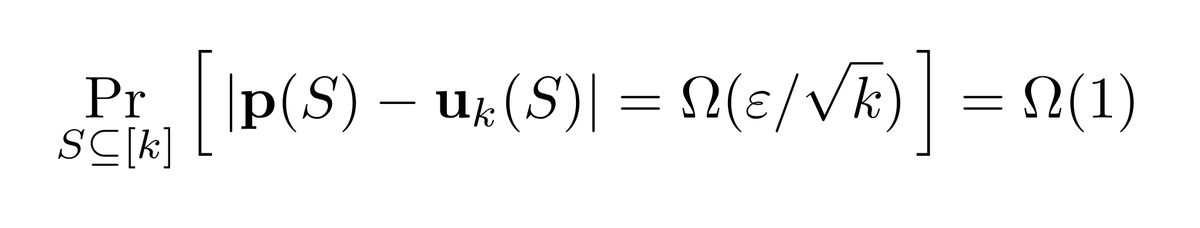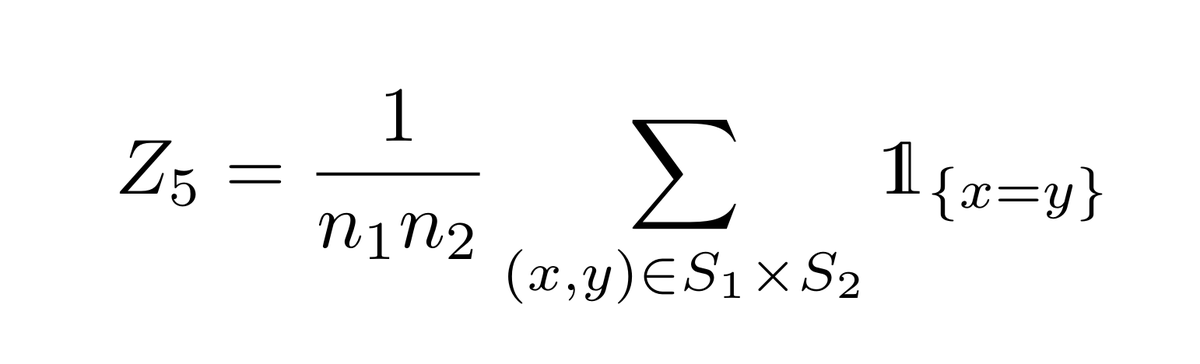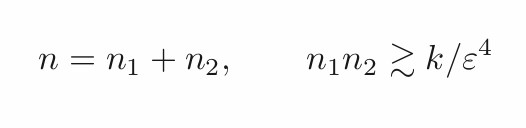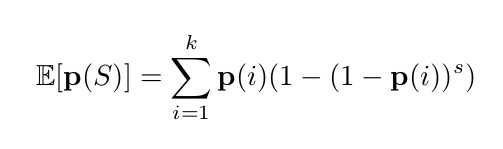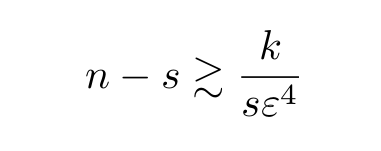Be careful what you wish for :) #statistics
1/n
2/n
en.wikipedia.org/wiki/Total_var…
The latter... is below.
3/n

4/n
So... how do we do that with only √k/ε² samples?
8/n
Getting √k/ε².. *much* harder. "Simplicity" ☐
11/n
Which is a uniquely good segue for our *second* algorithm, based on a dual-ish idea: counting the unique elements instead! #nocollision
12/n
A few tricks can help us: e.g., Efron—Stein: en.wikipedia.org/wiki/Concentra…
14/??
Why? 🤔
15/n
So we need n ≪ k, or things start to break. Since n≍√k/ε², that gives ε≫1/k¼...
16/n
Data efficient ☑️
Time efficient ☑️
Simple + "simple" ☑️
Elegant ☑️
... but has a restriction on the parameters ☐
17/n
18/n
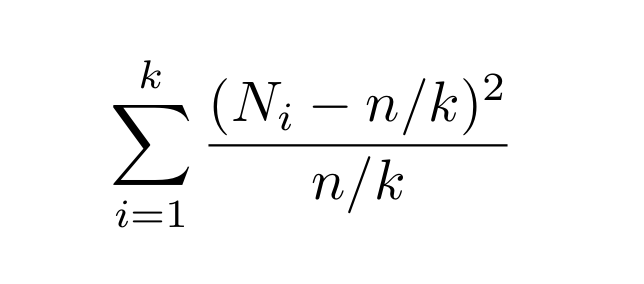
20/n
Data efficient ☑️
Simple ☑️
"Simple" ☑️
Fast ☑️
Intuitive ☐
Elegant ☐
22/n
Carefully analyzing this tiny gap in 𝔼+showing that Z₄ concentrates well enough to preserve it... works!
25/n
The analysis is not really simple, though...
Data efficient ☑️
Simple ☑️
"Simple" ☐
Fast ☑️
Intuitive ☐
Elegant ☑️
26/n
💡If there is one thing we know how to do, it's estimating the bias of a coin. We don't have a coin here, we have a glorious (k-1)-dimensional object.
27/n
Hash all the n samples you got: NOW we have a random coin!
28/n
Not optimal, but... pretty fun.
Data efficient ☐
Memory efficient ☑️
Simple ☑️
"Simple" ☑️
Fast ☑️
Intuitive ☑️
Elegant ☑️
30/n
In the meantime: what do you care more about?
In our first, "collision-based" algorithm, recall that we took a multiset S of n samples from p and looked at the number of "collisions" in S to define our statistic Z₁. That gave us an estimator for ||p||₂²...
31/n
Not bad!
Data efficient ☑️
Simple ☑️
"Simple" ☐
Fast ☑️
Intuitive ☐
Elegant ☐
34/n
Fix s < n. Take n samples from p, and consider the set S (not multiset) of by the first s samples.
35/n
OK, there is the same slight bummer as in the "unique elements" algorithm: we need s ≪ k in the first stage (can you see why?), so overall this requires ε ≫ 1/k¼. Oh, well.
38/n
Data efficient ☑️
Memory efficient ☑️
Simple ☑️
"Simple" ☐ (jury's still out)
Fast ☑️
Intuitive ☑️
Elegant ☑️
Yes, I'm a bit biased, I know.
39/n
I'll put up a 📝 summary soon. In the meantime, here are a subset of the algorithms mentioned: which one do *you* prefer? 🙋
40/end