
Senior Lecturer @Sydney_Uni. Formerly Postdocs @IBMResearch, @Stanford; PhD @Columbia. Converts ☕ into puns: sometimes theorems. He/him. @ccanonne.bsky.social
How to get URL link on X (Twitter) App


https://twitter.com/ccanonne_/status/1555317803011698688Let's start with a PSA: print this. Hang it on the wall near your desk. Make it a t-shirt and wear it to work. lkozma.net/inequalities_c…




 Answered in the affirmative in 2005 by Ravi B. Boppana (and made available in 2020 on arxiv.org/abs/2007.11017.)
Answered in the affirmative in 2005 by Ravi B. Boppana (and made available in 2020 on arxiv.org/abs/2007.11017.)


 This was part of the "Winter/Summer Research Internship" program at @Eng_IT_Sydney @Sydney_Uni:
This was part of the "Winter/Summer Research Internship" program at @Eng_IT_Sydney @Sydney_Uni: https://twitter.com/ccanonne_/status/1421356007255547911

https://twitter.com/ccanonne_/status/1428356267215446017Greedy #algorithms can be surprisingly powerful, on top of being very often quite intuitive and natural. (Of course, sometimes their *analysis* can be complicated... but hey, you do the analysis only once, but run the algo forever after!)

https://twitter.com/ccanonne_/status/1372702428110327808Note that this is true for only two r.v.'s: if X~X' and Y~Y'


https://twitter.com/ccanonne_/status/1374909562470297603
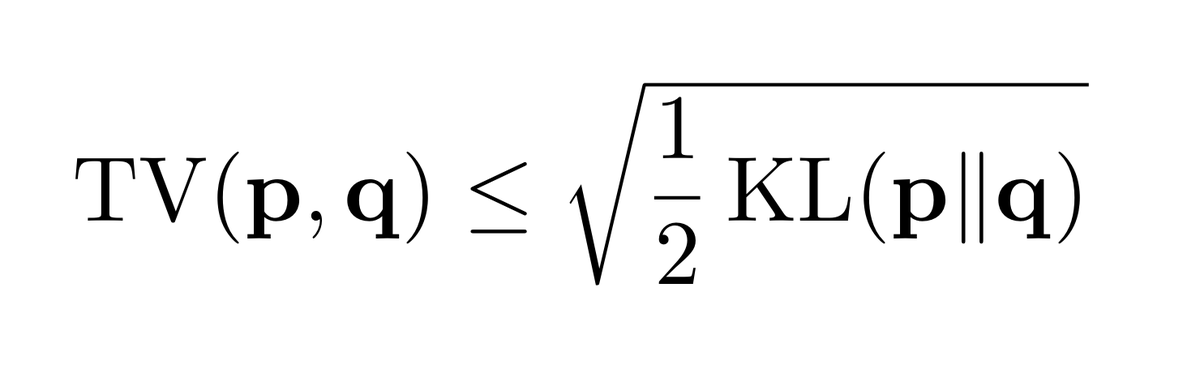
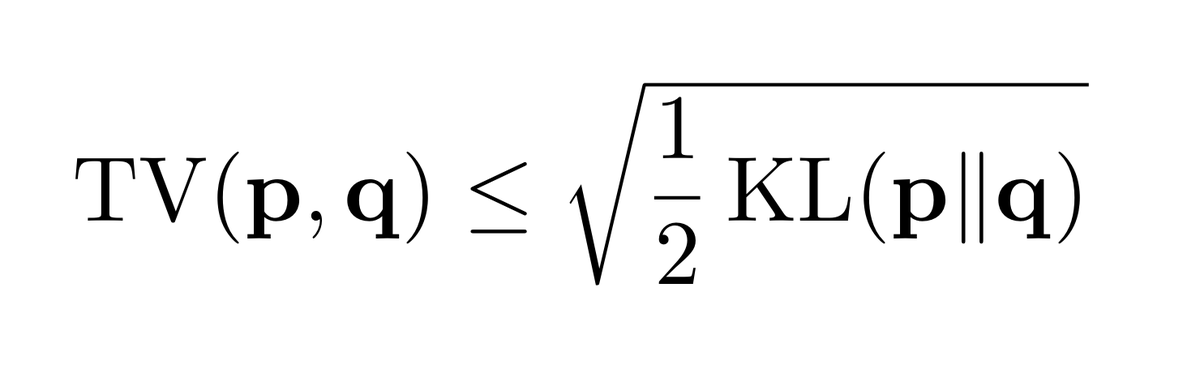 It's warranted: a great inequality, and tight in the regime where KL→0. Now, the issue is that KL is unbounded, while 0≤TV≤1 always, so the bound becomes vacuous when KL > 2. Oops.
It's warranted: a great inequality, and tight in the regime where KL→0. Now, the issue is that KL is unbounded, while 0≤TV≤1 always, so the bound becomes vacuous when KL > 2. Oops.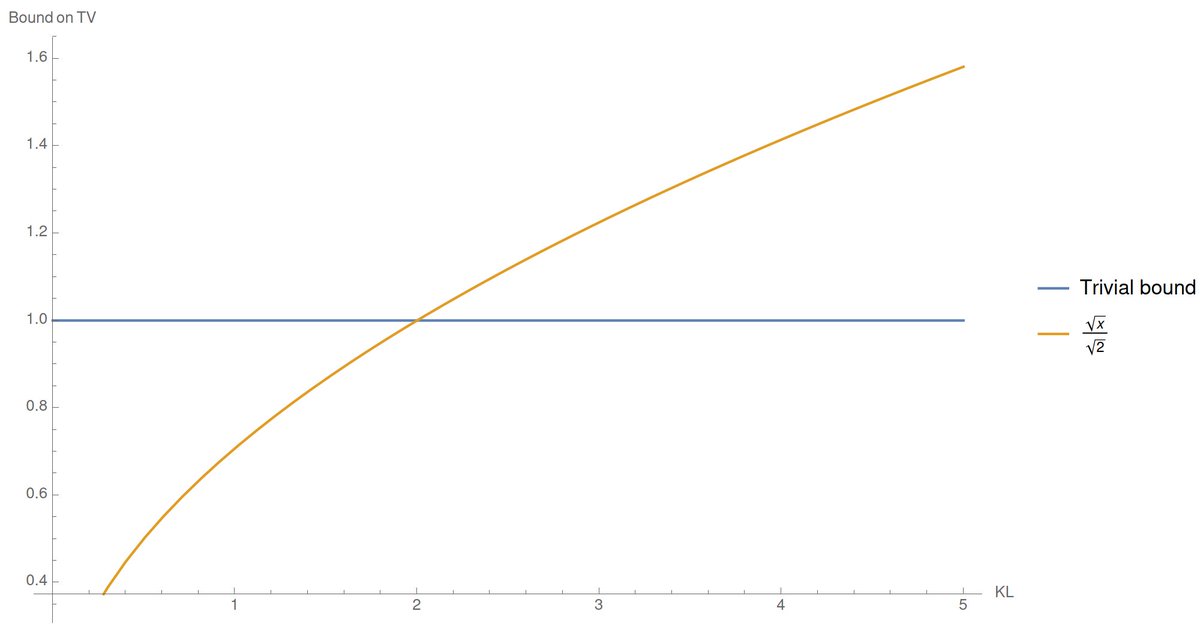

https://twitter.com/ccanonne_/status/1334486719769481218So, the first question... was a trap. All three answers were valid...
https://twitter.com/ccanonne_/status/1334486724374908928
https://twitter.com/BellLabs/status/1334552036084420611Will Carlini et al. get a share of the prize money for breaking the system prior to the award ceremony? arxiv.org/abs/2011.05315



https://twitter.com/ccanonne_/status/1285114718928039936Suppose you have the following type of measurements: at each time step, you get to specify a subset S⊆[k], your "question"; and *try* to observe a fresh sample x from the unknown distribution p (over [k]). With probability η, you get to see x: it's leaked to you 🎁...

https://twitter.com/ccanonne_/status/1283237083260137474So.... uniformity testing. You have n i.i.d. samples from some unknown distribution over [k]={1,2,...,k} and want to know: is it *the* uniform distribution? Or is it statistically far from it, say, at total variation distance ε?

https://twitter.com/ccanonne_/status/1281129193187598337
https://twitter.com/ccanonne_/status/1281129204369600512

https://twitter.com/ccanonne_/status/1278729297436368899
https://twitter.com/ccanonne_/status/1278729301387444225

https://twitter.com/ccanonne_/status/1276058248206938113
 Central to their study is the corresponding Fourier transform: each such f is uniquely determined by the truth table of its 2ⁿ values, or, equivalently, by the list of its 2ⁿ Fourier coeffs f̂(S), one for each S⊆[n].
Central to their study is the corresponding Fourier transform: each such f is uniquely determined by the truth table of its 2ⁿ values, or, equivalently, by the list of its 2ⁿ Fourier coeffs f̂(S), one for each S⊆[n].