I would like to claim my Nobel Prize please.
For curing cancer.
Can you post me my medal, or do I have to come and collect it in person?
#FOAMED #MedTwitter #Tweetorial

The method of curing cancer I have developed is as follows.
Well, take them at night.
That's it.
(Or maybe D, I suppose, if you used Google Translate to do the poll.)
"Don't tell unnecessary lies."
"Judge Sahib says, you must tell lies only when it is necessary".
How many died in total?
[Since only a small proportion of the participants died, and followup was pretty complete...]
Which of the following is your best estimate for the RISK ratio for mortality. Also called relative risk or probability ratio.
Probability of death may be 99%. But this is only 9 percentage points higher.
Suppose the mortalities are 90 and 99% respectively.
RR is only 1.1.
Being very dangerous (in risk, aka probability terms) prevents anything being more dangerous in comparison.
Obviously they can't just do it for big probabilities, and leave small probabilities alone. That would create a discontinuity.
They have to smoothly stretch.
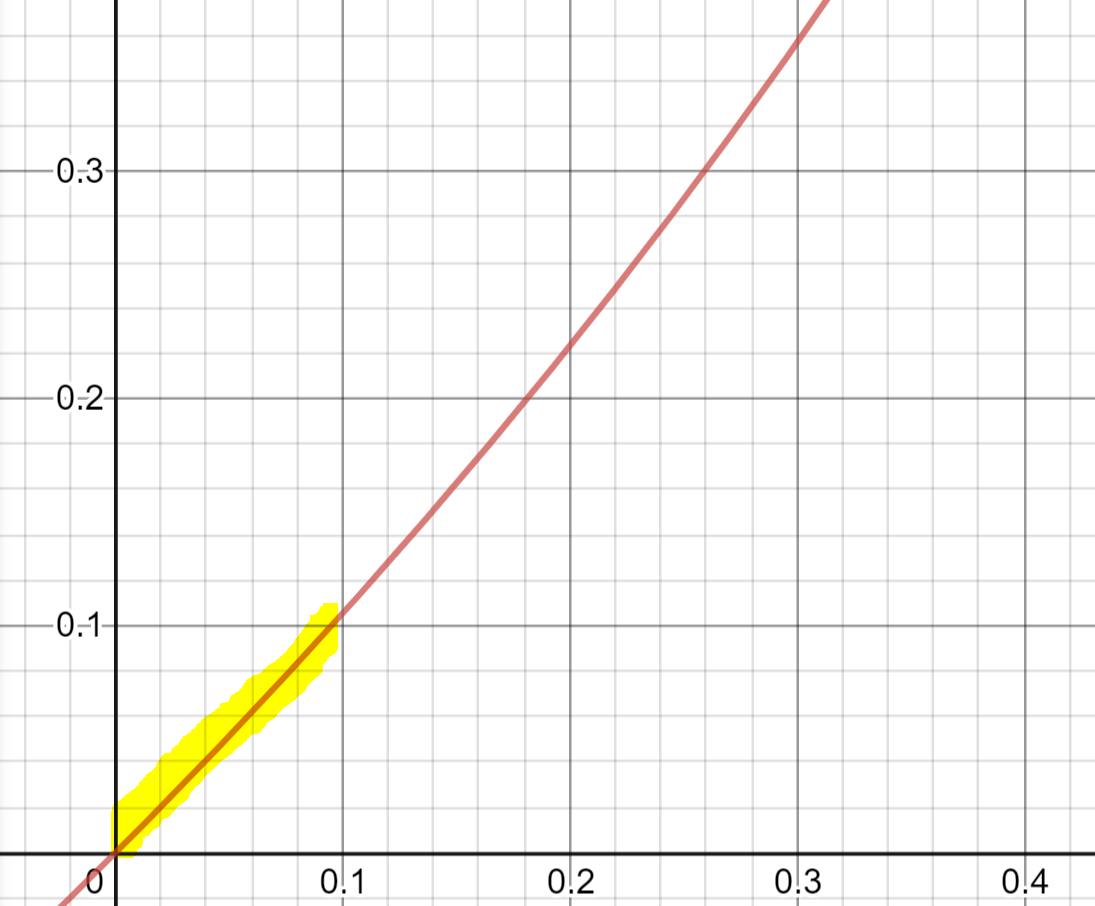
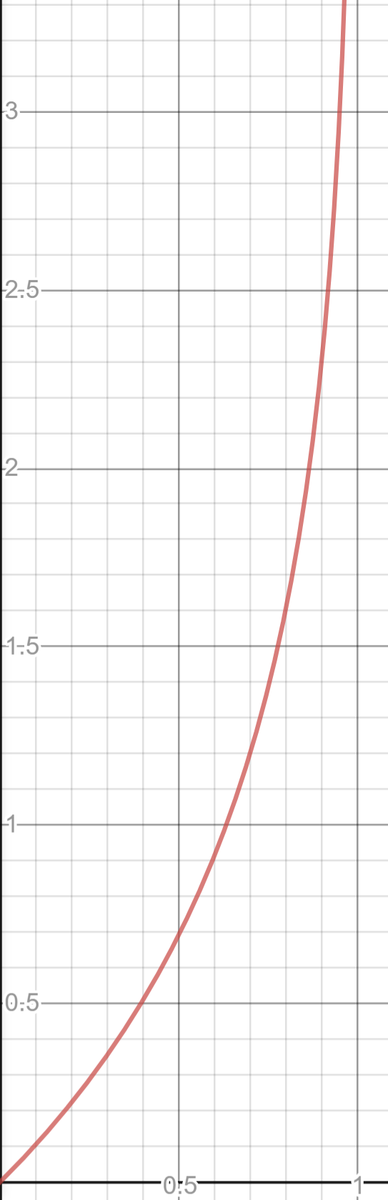
y = - ln(1-x)
By the chain rule,
dy/dx
= -1 * 1/(1-x) * d/dx(1-x)
= 1/(1-x)
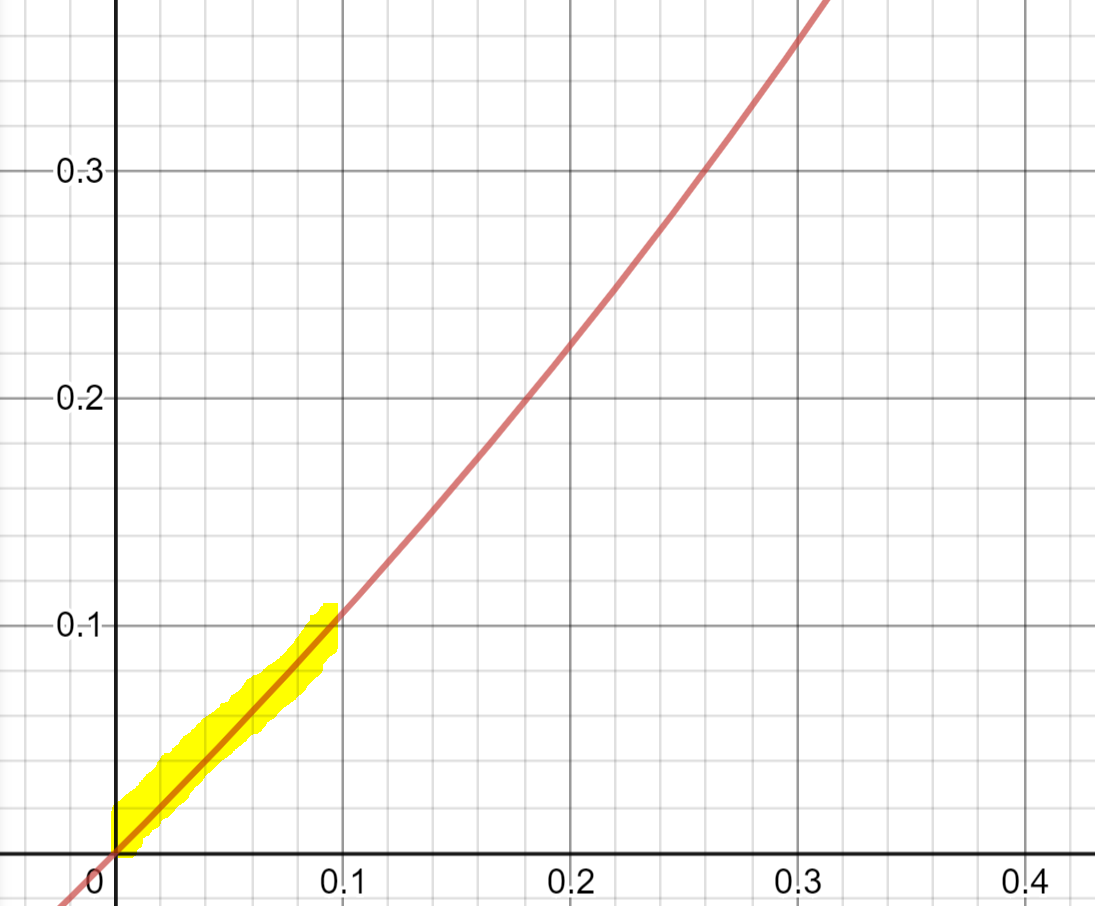
For low probabilities,
hazard is almost exactly the same as probability.
And as probability increases, the curve gets steeper in proportion to 1/(1-probability).
90% chance of death is what HAZARD of death?
- ln(1-0.9) is what?
Hint: lmgtfy.com/?q=-ln(1-0.9)
Shouting abuse at Iqbal Malik and then vomiting at NHS England, saying "How about that for an aerosol?"
Convert 0.99 probability to a HAZARD.
- ln (1-0.99) is what?
Hint: google.com/search?q=-ln(1…
It is exact because that is exactly what hazards do.
They allow linear combinations of dangerous things, like a 100 mile journey and then another identical journey, to add up linearly, rather than get squashed up at 1.
That's the main point of today!
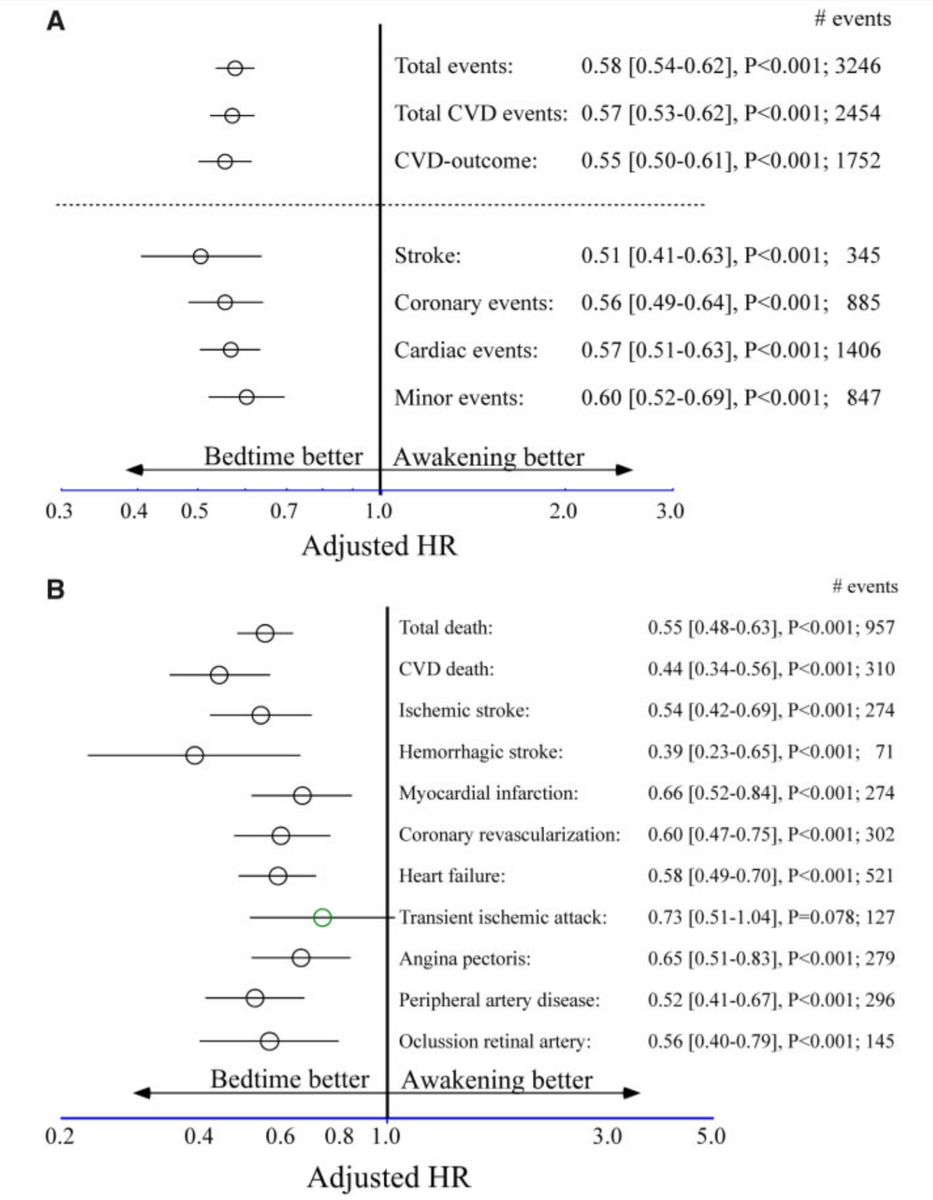
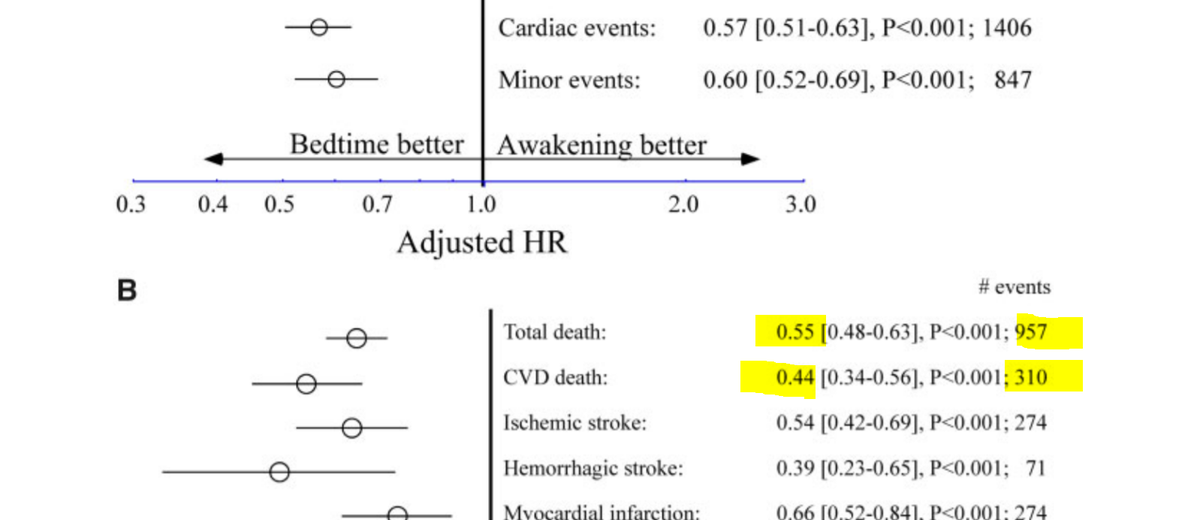
About 20k patients and 1k deaths.
Probability of death was therefore (choose the option that best describes the answer):
So the numbers of deaths in each arms will be approximately
957 *0.55/1.55 and 957 * 1/1.55 respectively,
i.e.
340 and 617.
How many in the active arm?
How many non-cardiovascular deaths in each arm?
245 in the active, and 402 in the control!
What's the hazard ratio, roughly?
What a hilarious thing to see in a journal.
I absolutely love it.
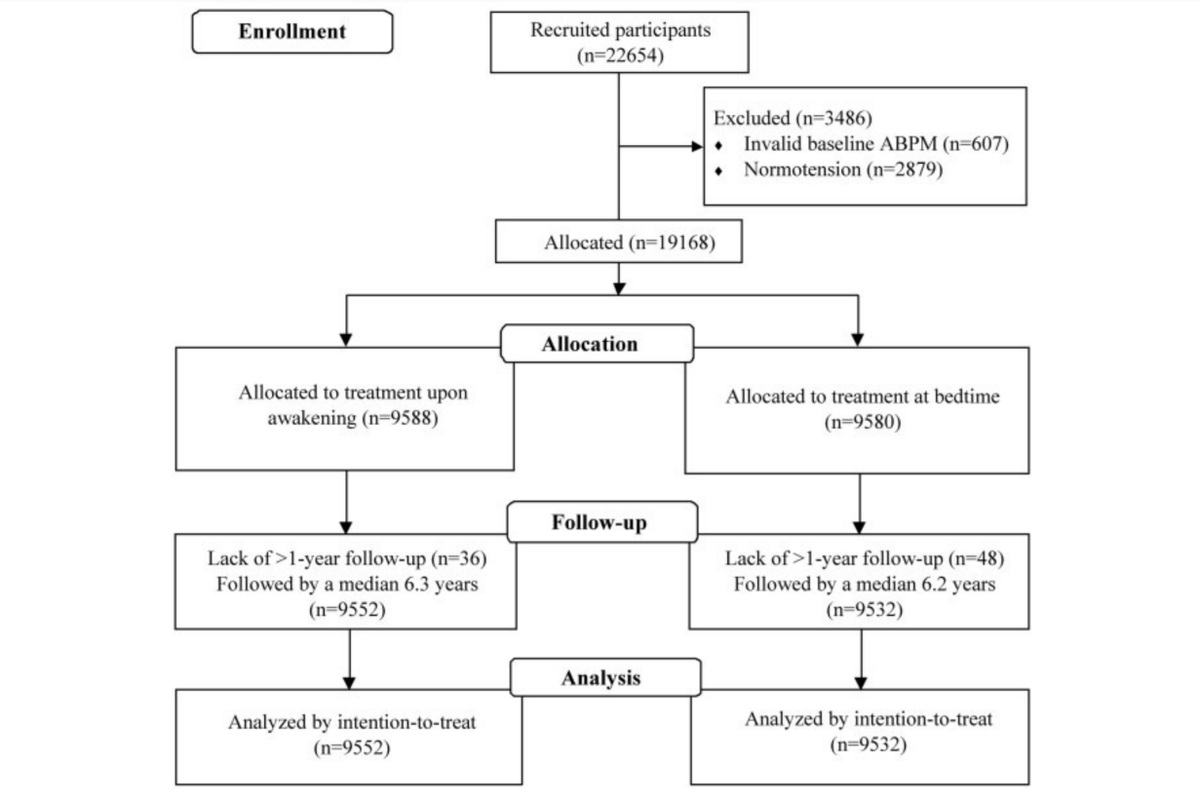
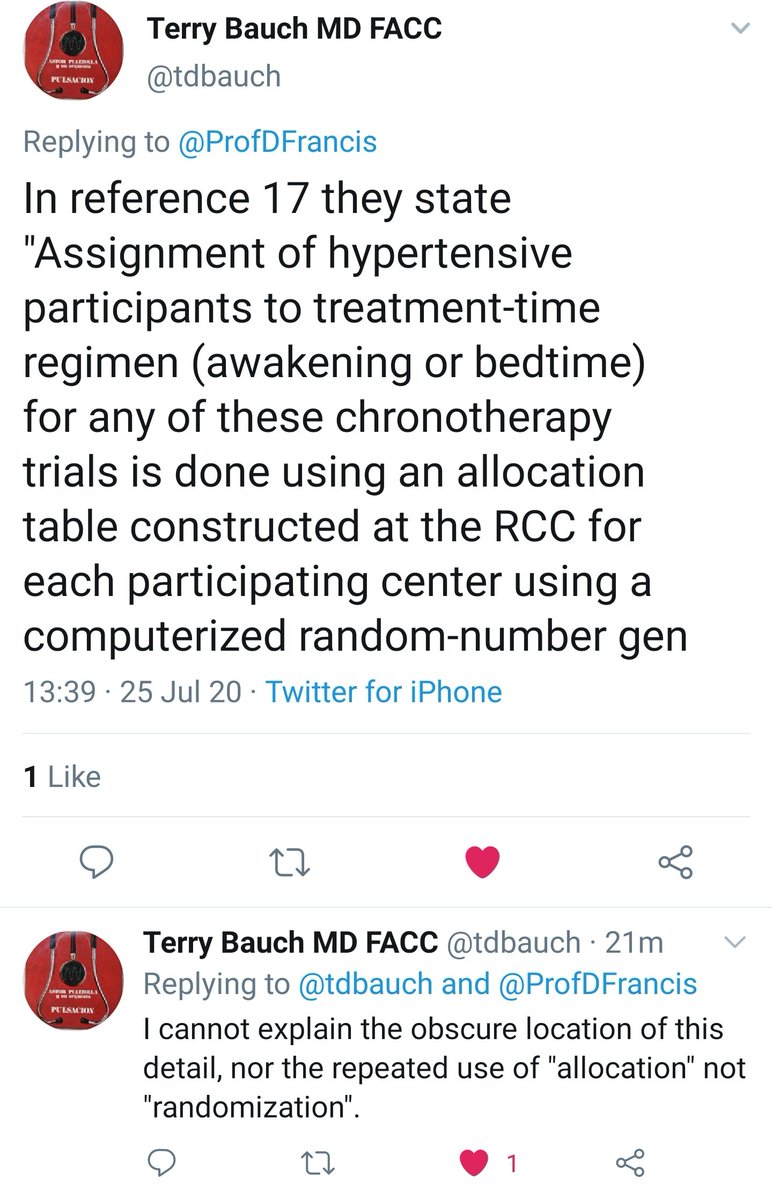
Hypothesis 1. It wasn't really randomized. They just said it was.
My reasoning for this is that they tried really hard to avoid mentioning randomization.
Actually I've forgotten what my alternative hypothesis was. I am sure I had another explanation, but was
The easier we allow them to suddenly remember that it wasn't randomized, the easier it will be for them to get out of it, and the best for everyone.
Haven't heard back from Lancet for a couple of years on that one. Must prod them.
Suggests to me that it either wasn't an RCT at all.
Or was simply made up in its entirety.
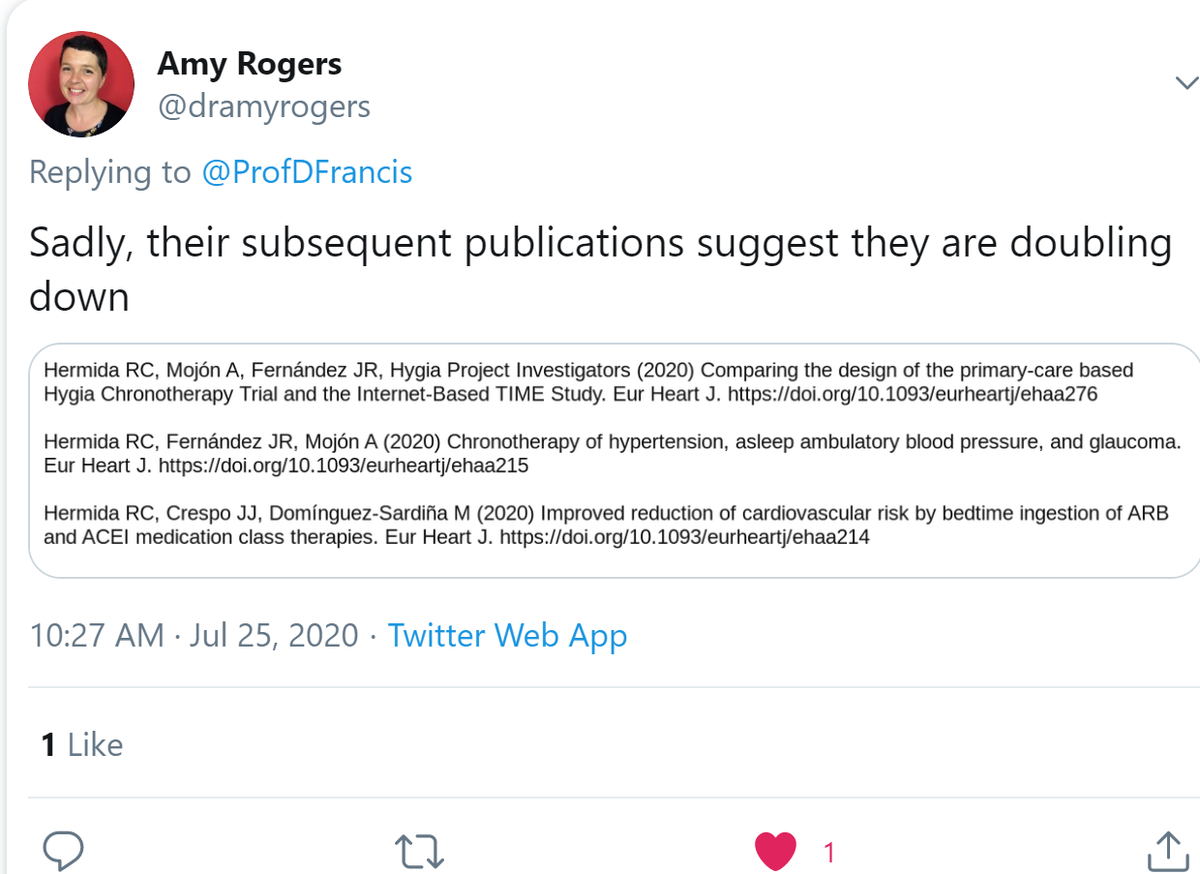
Swapnil Hiremath beat me to the Nobel!
Gaaah!
This is superb!
Can anyone suggest to me which serial fibber @drgrahamcole and I are hassling the Lancet over?
Strangely similar modus operandi.
Suppose we outsource all the lying to one particular paper. Then we can always just reference that paper. So we avoid telling any MORE lies.
It's Ok with you if I keep referencing an older off-balance-sheet lie, isn't it?
I was taught that by a friend in Wirecard.
Lovely chap.
Ok thanks.
For example, if you give people antihypertensives, you might prevent strokes etc, but cause more hypotension and resultant falls etc.
Initiating perioperative beta blockade DEFINITELY prevents MI, and deaths due to MI.
But it also increases other causes of death. By much more.
So total death goes up.
That would prevent cardiovascular death (because people who have died early because of the side effect, don't then live long enough to get their CV death)
That way we know we have either
(a) reclassified CV deaths as non-CV
or even
(b) caused more non-CV deaths than the CV deaths we prevent.
However, we never find that NON-CV deaths get DECREASED. That would be too amazingly good.
What do people die of, other than CV death?
Mainly cancer.
Plus a few other things.
You would publish it in a major *general* journal, e.g. Lancet / NEJM / JAMA
Or even the Bible.
They wouldn't just give old Hermida the Nobel Prize.
They would cancel the next 10 years of Nobels, and say all those medals would all be awarded to him.
THAT is how unbelievably amazing it is.
So he is either very modest.
Or didn't notice in his hasty fakery.
I think the latter. He is not only a fraudster, but an outstandingly incompetent one.
"I am the first in my trading block (of nobody) to say this."
Thank you B Johnson and N Farage