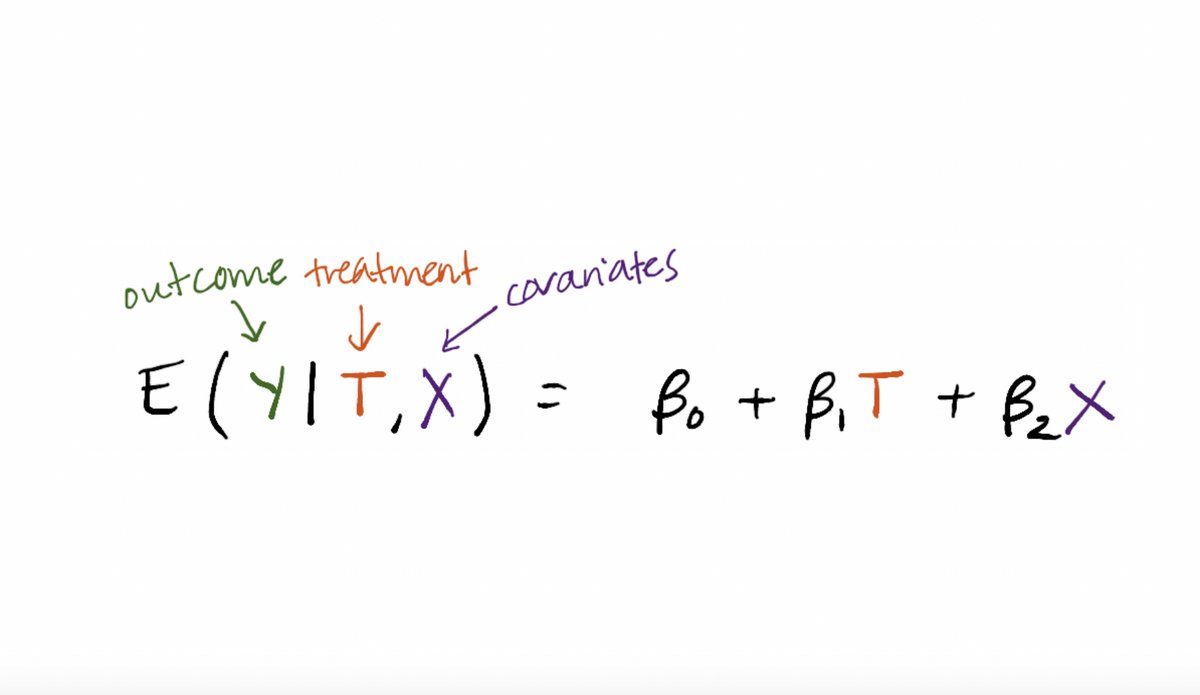Share this page!

Women in Statistics and Data Science Profile picture
Twitter logo
26 Oct, 6 tweets, 2 min read
What do professors do day-to-day (in a pandemic)?

This varies *a lot* by type of role, seniority, and institution.

I’m tenured at a research-intensive institution and I am not teaching this term.
I spend a fair amount of time meeting with students and collaborators. Today, Monday, I have 5 such meetings.

There are also lots of emails and administrative tasks all the time.
Each day this week I’ll drop a tweet in this thread to add in unique things I haven’t mentioned yet to demystify the life of this particular professor.
I just finished up my meetings for the day and there has been a lot of news in the world...

What I'll add to this thread is that today my cat Tobias joined 3 of my zooms. White and grey cat in a zoo...
Tuesday’s unique things: Conducting interviews and meeting with colleagues about our new summer diversity initiative!

(non-unique: Cat joining more research zooms…) Grey and white cat in a cir...
Wednesday's unique thing: Discussed the academic job market with a colleague and some senior graduate students! 🤓🧑‍💻🧑‍🏫

• • •

Missing some Tweet in this thread? You can try to force a refresh
　

Keep Current with Women in Statistics and Data Science

Women in Statistics and Data Science Profile picture

Stay in touch and get notified when new unrolls are available from this author!

Read all threads

This Thread may be Removed Anytime!

PDF

Twitter may remove this content at anytime! Save it as PDF for later use!

Try unrolling a thread yourself!

how to unroll video
  1. Follow @ThreadReaderApp to mention us!

  2. From a Twitter thread mention us with a keyword "unroll"
@threadreaderapp unroll

Practice here first or read more on our help page!

More from @WomenInStat

Women in Statistics and Data Science Profile picture
28 Oct
Tweetorial on going from regression to estimating causal effects with machine learning.

I get a lot of questions from students regarding how to think about this *conceptually*, so this is a beginner-friendly #causaltwitter high-level overview with additional references. Hand-drawn graphic of a reg...
One thing to keep in mind is that a traditional parametric regression is estimating a conditional mean E(Y|T,X).

The bias—variance tradeoff is for that conditional mean, not the coefficients in front of T and X. Hand-drawn graphic of a reg...
The next step to think about conceptually is that this conditional mean E(Y|T,X) can be estimated with other tools. Yes, standard parametric regression, but also machine learning tools like random forests.

It’s OK if this is big conceptual leap for you! It is for many people! Hand-drawn graphic of the c...
Read 13 tweets
Women in Statistics and Data Science Profile picture
8 Oct
🧵 time! I’d love to talk about the responsibilities we have as data practitioners. In this ~~information age~~ I think it’s critical we use data, ML, stats, and algorithms fairly, and with an eye toward making the world better for people.
I found this piece on data visualization very striking: medium.com/nightingale/it…
“Knowledge is never subjective.” As the creator of a graph, you hold the narrative power.
Read 11 tweets
Women in Statistics and Data Science Profile picture
7 Oct
Lots of people have asked me if studying biostats has actually been relevant in my career as a software engineer, and I’ve found the answer to be a resounding yes! It's super relevant in lots of engineering problems and in understanding the world generally. 🧵 follows!
When I worked on payment fraud prevention, I was always talking about diagnostic testing for rare diseases!
Diagnostic testing was something we studied at length in our early biostat & epi classes in grad school and it turns out “fraud” behaves similarly to a “rare disease” in a lot of ways.
Read 9 tweets
Women in Statistics and Data Science Profile picture
6 Oct
Gerrymandering gets its name from one Elbridge Gerry, who in 1812 drew a voting district in Boston that looked like a salamander because it was politically expedient.
the practice persists through today, from city council districts all the way up to (arguably) the Electoral College!
math, statistics, and measurement have played a key role in several court cases related to the ongoing discussion and fight for fair and representative districts.
Read 6 tweets
Women in Statistics and Data Science Profile picture
4 Sep
One more quick tweet, unrelated to the Gelman-Rubin diagnostic.

Someone asked, "I hear C++ is fast but a little hard to grasp. That true?"

Mostly yes. Like Python, R is mostly easier to learn and often is slower than C/C++.
I recommend you think about how your code will be used when you decide what language to code in. If you're coding for yourself and you probably just need to run it once, then R may be a good choice. Optimizing for speed may be overkill. (2/)
If you are writing a function/package for public consumption, then speed is much more of a concern. You can profile your code to see which parts are time-consuming. You can also just google what things R is slow at (ex loops). (3/)
Read 10 tweets
Women in Statistics and Data Science Profile picture
2 Sep
Let's extend the linear model (LM) in the directio of the GLM first. If you loosen up the normality assumption to instead allow Poisson, binomial, etc (members of the "exponential family" of distributions), then you can model count, binary, etc responses. (4/)
You've probably heard of Poisson regression or logistic regression. These fall under the umbrella of GLM. (5/)
The LM regression equation is E(Y) = X Beta, where X is the model matrix, Beta is the vector of coefficients, Y is the response vector, and E(Y) is the expected val.

For Poisson regression, we have log(E(Y)) = X Beta.
For logistic regression, we have log(p/(1-p))= X Beta (6/)
Read 16 tweets

Did Thread Reader help you today?

Support us! We are indie developers!

This site is made by just two indie developers on a laptop doing marketing, support and development! Read more about the story.

Become a Premium Member ($3/month or $30/year) and get exclusive features!

Become Premium

Too expensive? Make a small donation by buying us coffee ($5) or help with server cost ($10)

Donate via Paypal Become our Patreon

Thank you for your support!

Follow Us on Twitter!

Like this author's thread?

Get email notifications when new thread is out from this Author!

Check out other threads from this Author!

Read all threads by @WomenInStat