Thread by @Inaki_Huarte

Entre las medidas tomadas para detener la propagación del COVID-19, hay una particularmente interesante:

⚠️ Mantener una distancia social de 1-2 metros 🚶 🚶

Hoy nos metemos de lleno en esta medida y os cuento nuestro último trabajo, ¿pasas? #VaHilo #COVID19 #ComunicaTuCiencia

Empecemos con una pregunta: Cuándo nos movemos, ¿crees que somos capaces de mantener la distancia social?

Probablemente pienses que no. Al fin y al cabo, solemos caminar algo desprevenidos respecto a esto.

Pero, y si nos dicen que nos concentremos en hacerlo, ¿podríamos?

Nuestra respuesta fue clara:

💡¡Hagamos un experimento para ver qué pasa! 💡

👉 Vamos a meter a un grupo de personas dentro de un recinto a hacerlas caminar intentando mantener una distancia social de X metros con el resto y ver qué ocurre🚶🚶🚶

¿Qué parámetros vamos a cambiar?

1️⃣ Densidad: Número de gente dentro del recinto.
2️⃣ Velocidad: ¿Qué diferencia hay entre caminar rápido o lento?
3️⃣ Distancia de seguridad: Probaremos 2 y 1.5 metros.¿Habrá alguna diferencia?

En total se probaron 12 configuraciones distintas. Puedes encontrar un resumen en la tabla de abajo ⤵️

Todos los experimentos los codificamos con el número de personas y su velocidad. Así, 12S por ejemplo marca el experimento con 12 personas y velocidad de paso lenta (S de slow)

Veamos un ejemplo de estos experimentos. En este caso son:

1️⃣ 24 personas
2️⃣ Caminando lento
3️⃣ Intentando mantener una distancia de 1.5 m

A partir de estos vídeos, conseguimos obtener las posiciones y velocidades de cada peatón durante todo el experimento.

La flechas encima de sus cabezas indican la velocidad de cada persona (basadas en la escala de la flecha negra de arriba a la dcha de 1 m/s)

Y con los datos de posiciones y velocidades, ¿qué podemos medir? Pues en nuestro caso ha sido

🔹 Distancia al vecino más cercano
🔹 Velocidad de cada persona
🔹 Tiempos de exposición: Tiempo que 2 peatones están a una distancia menor de 1.5 m

Comencemos por lo más importante. La distancia al vecino más cercano = Distancia Social

Vamos a ver la distribución de los valores registrados ¿Consiguieron o no respetar una distancia de 2 metros? ¿Apuestas?

🔹Con 2 metros de distancia social y sólo 12 peatones (densidad + baja probada), un 50% de la gente no lo respetó.
🔹Aumentar el número de personas (de 12 - roja - a 18 - azul -) creó + infracciones
🔹Caminar + rápido hizo que la distancia al vecino fuese menor.

Reducir la distancia social de 2 a 1.5 nos permitió introducir un mayor número de personas (hasta 32)

Aún así, se mantuvo el mismo comportamiento que el que hemos comentado para 2 m

🔹Un aumento de la densidad y de la velocidad hizo más difícil respetar la distancia social🔹

Pero, ¿qué es mejor decir a la gente: que respete 2 o 1.5 metros?

Vamos a comprobarlo calculando el tiempo durante el cual un peatón tiene a una persona a menos de un metro (acercamiento excesivo)

Fijaros sobre todo en los casos de 18 y 24 personas (centro de la gráfica)

Si os dais cuenta, de forma sistemática los círculos están por debajo de los cuadrados si comparamos rellenos por un lado y no rellenos por otro (misma velocidad)

Esto nos indica que es mejor sugerir una distancia social mayor o, en otras palabras, es mejor establecer 2 m de distancia social que 1.5 m.

Hemos podido comprobar que sugerir distancias sociales menores hace que nuestros acercamientos sean más próximos.

Veamos ahora los valores de velocidad:

🔹Se ve una clara diferencia entre los experimentos fast y slow
🔹Para el caso lento, un aumento de la densidad (mira curvas ♥️ y 💚) origina menores valores de velocidad.
🔹Esto no se ve para el caso rápido donde las 3 curvas se solapan

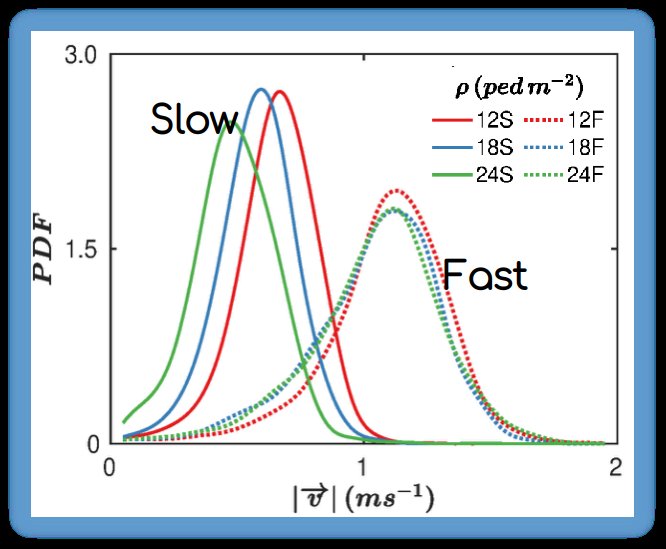
Esto es bastante interesante. Parece ser que el hecho de caminar rápido hace que nuestra percepción global del entorno se reduzca, haciendo que no diferenciemos entre un sistema denso o no.

Veamos por último los tiempos de exposición. Recordemos que esta variable me va a decir el tiempo durante el cual dos personas están a menos de 1.5 metros.

Encontramos dos tendencias claras:

🔹Aumentar el número de peatones hace que los tiempos de exposición crezcan.

🔹Aumentar la velocidad origina tiempos de exposición menores.

🔹Ambas tendencias se mantienen si reducimos la distancia de seguridad de 2 a 1.5 m

Ambas conclusiones son más o menos coherentes. Lo que es más interesante es lo siguiente 👇

Si cogemos cada curva y la multiplicamos por el valor medio de la velocidad registrada durante ese experimento, se obtiene la siguiente gráfica. ¿Ves como la mayoría de curvas se solapan?

Hemos conseguido un colapso de las curvas 😍

Con ello, podemos definir una valor característico de nuestro sistema. En nuestro caso será una distancia (tiempo x velocidad = distancia) Concretamente será aprox 1 metro (máximo de las curvas)

Esta distancia la interpretamos como la distancia que necesita una persona para resolver el conflicto de acercamiento y volver a una posición en la que esté respetando el distanciamiento social.

Creo que por hoy es suficiente 😅

Vamos a resumir en la siguiente imagen todo lo que hemos visto 👇

Entérate un poquito más (y seguro que mejor) de nuestro último trabajo en el siguiente link.

Muchas gracias por haber llegado hasta aquí 🤗 Nos leemos y seguimos contando ciencia! 👩‍💻

Cuidaros 🤜👑🦠

🔗 nature.com/articles/s4159…