Share this page!

黒木玄 Gen Kuroki Profile picture
Twitter logo
22 Jan, 9 tweets, 5 min read
#Julia言語

nbviewer.jupyter.org/gist/genkuroki…
QuadGK, Optim, Roots, Memoize, NLsolve の使用例

QuadGK.jl 1変数函数の数値積分
Optim.jl 函数の最小化
Roots.jl 1変数函数の零点
Memoize.jl メモ化
NLsolve.jl 非線形(連立)方程式の解法

この手の基本的なパッケージの使い方を知っていると楽をできます。
#Julia言語

∫_0^1 ζ(s, x+t) dt = 1/((s-1)xˢ⁻¹) の数値的確認.

数値積分に QuadGK.quadgk を使用。私の場合には、自前で数値積分のコードを書くより、楽で同精度なら速いことが多いです。
#Julia言語

Optim.optimize を使ったベータ分布の最尤法

Distributions.jl の fit(Beta, sample) は最尤法でない推定法を採用しており、グラフを見れば分かるように誤差が大きくなる場合があります。
#Julia言語

2×2の分割表のFisher検定の実装例

Roots.find_zeros を使って、Fisher検定と整合的なオッズ比の信頼区間を求めています。

Rのfisher.testが表示する信頼区間はP値と整合性がありません。
#Julia言語

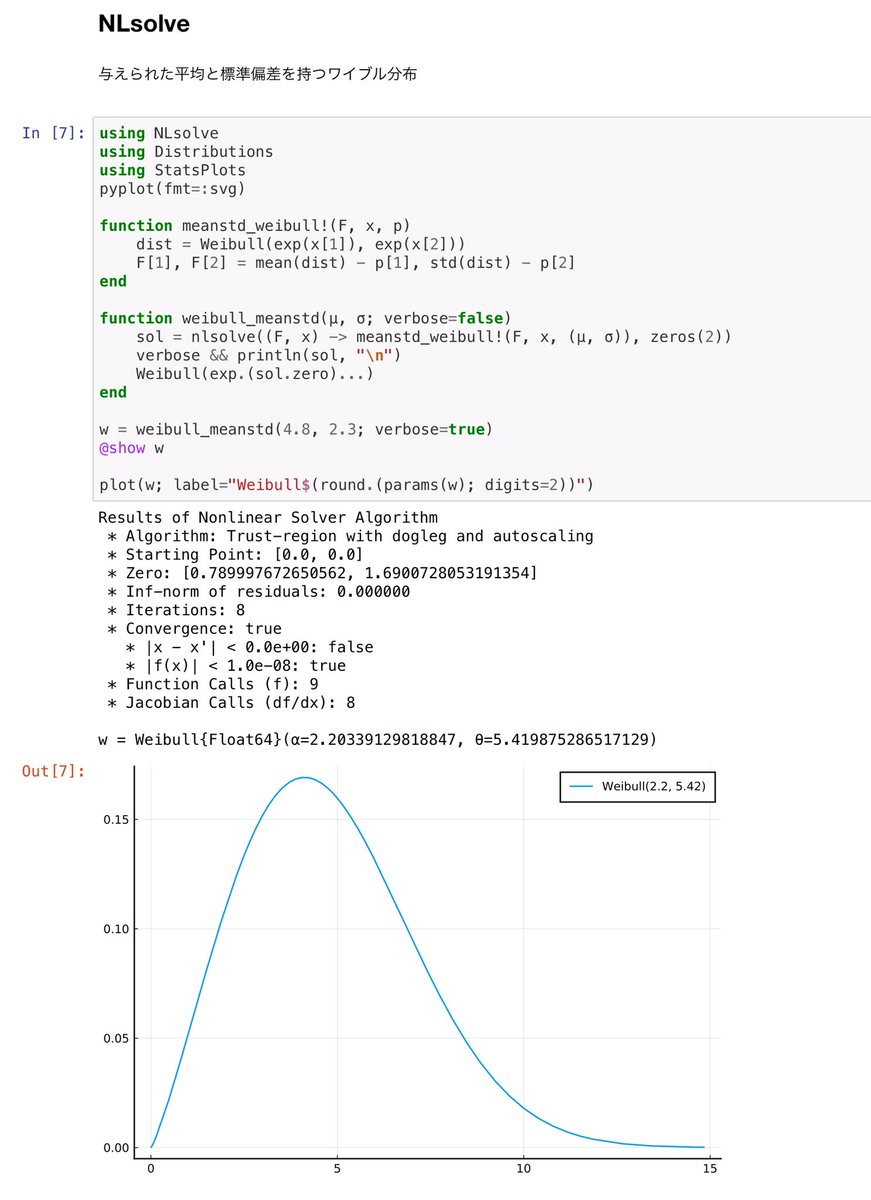
①与えられた平均と分散を持つWeibull分布をNLsolve.nlsolveを使って計算

②Weibull分布の最尤法をOptim.optimizeで実装

連立方程式をNLsolve.jlで解いたり、函数の最小化をOptim.jlで行ったりできます。もちろん、慎重な注意が必要な場合があります。
#Julia言語

計算結果をFisherText型のオブジェクトに格納するようにしてある。

添付画像

①FisherText型のオブジェクトのデフォルトでのテキスト表示とグラフ作画の仕方の設定

②Fisher検定の結果resultが自動的に清書されて表示され、plot(result)だけでグラフも表示

nbviewer.jupyter.org/gist/genkuroki…
#Julia言語

自分で定義した型のデフォルトでのテキスト表示の仕方の設定については以下のリンク先を参照。これ、非常に便利です。

docs.julialang.org/en/v1/manual/t…

docs.julialang.org/en/v1/base/io-…
#Julia言語

自分で定義した型の Plots.jl におけるデフォルトでのプロットの仕方の設定については以下のリンク先を参照。

これも非常に便利です。この機能があるので、PyPlot.jl とは別に Plots.jl も使いたくなる。

docs.juliaplots.org/latest/recipes/
訂正

❌FisherText
⭕️FisherTest

• • •

Missing some Tweet in this thread? You can try to force a refresh
　

Keep Current with 黒木玄 Gen Kuroki

黒木玄 Gen Kuroki Profile picture

Stay in touch and get notified when new unrolls are available from this author!

Read all threads

This Thread may be Removed Anytime!

PDF

Twitter may remove this content at anytime! Save it as PDF for later use!

Try unrolling a thread yourself!

how to unroll video
  1. Follow @ThreadReaderApp to mention us!

  2. From a Twitter thread mention us with a keyword "unroll"
@threadreaderapp unroll

Practice here first or read more on our help page!

More from @genkuroki

黒木玄 Gen Kuroki Profile picture
23 Jan
オンライン授業の整備について語る場合には

* そのために増える仕事をやる人を新たに雇うための予算
* 新たな設備投資のための予算

の確保のために、

* 日本政府の財政赤字を大幅に増やすことにも同時に賛成

しないと、一部の人たちに無理な要求を押し付けるだけで終わってしまうと思います。
自分自身が財政赤字が悪だと思っていたせいで次世代の未来を奪って来たことを正直に認めることができる人が増えれば、やれることが増えます。

ただし、MMTな人達はおかしなことも言っているので要注意。

あと、藤井聡氏は反医療の人たちと組んで反省していないようなので要注意人物確定済み。
失業率1%の上昇で年間自殺者数は2000〜3000人くらい増えると推定されます。(以前大雑把に計算した。ググっても確認した)

HPVワクチンの恩恵を受けられないと年間1000人以上の死者が増えるらしい。(これもググって確認した)

おそらく、反ワクチン・反医療と経済問題が殺す人数が似たオーダーです。
Read 10 tweets
黒木玄 Gen Kuroki Profile picture
23 Jan
#統計 以下のリンク先の例ほど極端な場合は稀だと思いますが、母集団が複数の質の異なった集団の和集合になっている場合はよくあります。

例えば共通テストでは、浪人生の集団の方が現役生よりも平均的な学力は上です。

このような場合には得点分布は正規分布には全然近くならない。
#統計 異なる質の集団の混合分布の具体例

ct.u-tokyo.ac.jp/news/20190210-…
↓
ct.u-tokyo.ac.jp/images/koudai-…
↓
pp.29-36
荘島宏二郎
センター試験「英語」はどのような試験だったか
【(スライド 3)～ここの右のほうのコブは浪人生です～浪人生を取り除くと割と左右対称な現役生 の分布が出てきます。】(p.30) ImageImage
#統計 複数の異なる質の集団の混合分布の「推定」を行う場合には、正規分布モデルを使ったりせずに、その通りの意味を持つモデルを使うべきだと思います。

例えば各部分集団の分布が正規分布で近似できそうなら、混合正規分布モデルを使ってみるとか。
Read 5 tweets
黒木玄 Gen Kuroki Profile picture
20 Jan
#Julia言語 Dictのプロット

ポイント：Dict型のdにはkeys(d)だけではなく、values(d)も定義されている。

Juliaのメソッド群は

a = []
for k in keys(d)
append!(a, d[k])
end

のようなコードを書かなくてもよいようになっている。

aがVector{Any}型になるのも嫌。

gist.github.com/genkuroki/ef0c… Image
#Julia言語 Juliaの型システムへの理解に自身がない場合には

function f(x, y)
～
end

struct Foo{A, B}
a::A
b::B
end

のように書いて、Float64とか、Arrayのような型名を書かずに済むようにすることがお勧め。

理解不足で型名を書くと、色々悪いことが起こる。何度も失敗した。
#Julia言語 例えば

struct Foo
a::Float64
b::Vector{Complex}
end

のように書いてFoo型を使うと、計算速度が数十倍オーダで遅くなる。

ComplexはComplexF64などであるべき。

考えずに済む解決策は

struct Foo{A, B}
a::A
b::B
end

具体的な型はJuliaに決めさせるとよい。 Image
Read 10 tweets
黒木玄 Gen Kuroki Profile picture
20 Jan
#数楽

Xを[0,1]上の一様分布に従う確率変数とすると、その分配函数(モーメント母函数)は

Z(β) = E[exp(-βX)] = (exp(-β) - 1)/(-β).

これの逆数が β/(1 - e⁻ᵝ).

カノニカル分布の密度函数

p(x) = exp(-βx)/Z(β)

はBernoulli多項式の母函数。続く
#数楽 [0,1]上の一様分布をℝ上の適切な弱い条件を満たす任意の分布に一般化することによっても、Hurwitzのゼータ函数やBernoulli多項式を一般化できる。

正規分布の場合のBernoulli多項式の類似物はHermiteの多項式になり、正規分布に対応するHurwitz型ゼータ函数の特殊値として出て来る。
#数楽 というような話よりもずっと色々なことが

nbviewer.jupyter.org/github/genkuro…
Hurwitzのゼータ函数の話

に書いてあります。
Read 6 tweets
黒木玄 Gen Kuroki Profile picture
20 Jan
【こわい人たちの議論に巻き込まないで🥲】←有害なトンデモ本の宣伝をしながら、こういうことを平気で言う？怖い😰

【P値の不適切解釈】については豊田『瀕死本』以外の文献にも書いてあります。

『瀕死本』がトンデモ本なのはP値の代わりに【仮説が正しい確率】の使用を勧めているからです。続く
豊田『瀕死本』ではP値ではなく【仮説が正しい確率】を使うことを勧めているのですが、【仮説が正しい確率】の具体例を見ると漸近的にP値と一致している数値になっていたりするので、この本は実質的にP値ではなくP値を使うことを勧めていることになっています(笑)。続く
例えば豊田『瀕死本』の図5.2, 5.3のphc=「仮説が正しい確率」はそれぞれに対応するP値にほぼぴったり一致しています。

添付画像のグラフとソースコード nbviewer.jupyter.org/gist/genkuroki… を見て下さい。

この一致は偶然ではなく、一般的に成立しています。
Read 19 tweets
黒木玄 Gen Kuroki Profile picture
19 Jan
まさに数学教育の闇

kanielabo.org/edmath/thirdme…
RIMS研究集会　
教育数学の一側面－高等教育における数学の多様性と普遍性-
研究代表者：岡本和夫
副代表者：蟹江幸博
RIMS420号室，2018.2.13-2018.2.16
↓
大島　利雄（城西大学）
大学における数学教育の問題点と工夫
kanielabo.org/edmath/thirdme…
全然、関係ない話題と繋げてしまうことになるが、上で引用した大島さんの文章は【妖怪について扱った文章であるにも関わらず具体的な妖怪の実例がほとんど皆無で抽象論に終始している】の類のものとは正反対。

ものすごく具体的！
私は大島さん的な文章が好きで、意味のある具体例がない抽象的な文章は有害だと考えている。

数学の研究者間では、抽象化・一般化はやろうと思えば幾らでもできるので、価値ある抽象化・一般化であることを示す具体的な例を示さないとダメだという非常に良い習慣があると思う。例がショボいとアウト。
Read 24 tweets

Did Thread Reader help you today?

Support us! We are indie developers!

This site is made by just two indie developers on a laptop doing marketing, support and development! Read more about the story.

Become a Premium Member ($3/month or $30/year) and get exclusive features!

Become Premium

Too expensive? Make a small donation by buying us coffee ($5) or help with server cost ($10)

Donate via Paypal Become our Patreon

Thank you for your support!

Follow Us on Twitter!

Like this author's thread?

Get emails when @genkuroki has new unrolls!

Check out other threads from @genkuroki!

Read all threads by @genkuroki