
Here is a simple example of a machine learning model.
I put it together a long time ago, and it was very helpful! I sliced it apart a thousand times until things started to make sense.
It's TensorFlow and Keras.
If you are starting out, this may be a good puzzle to solve.
I put it together a long time ago, and it was very helpful! I sliced it apart a thousand times until things started to make sense.
It's TensorFlow and Keras.
If you are starting out, this may be a good puzzle to solve.
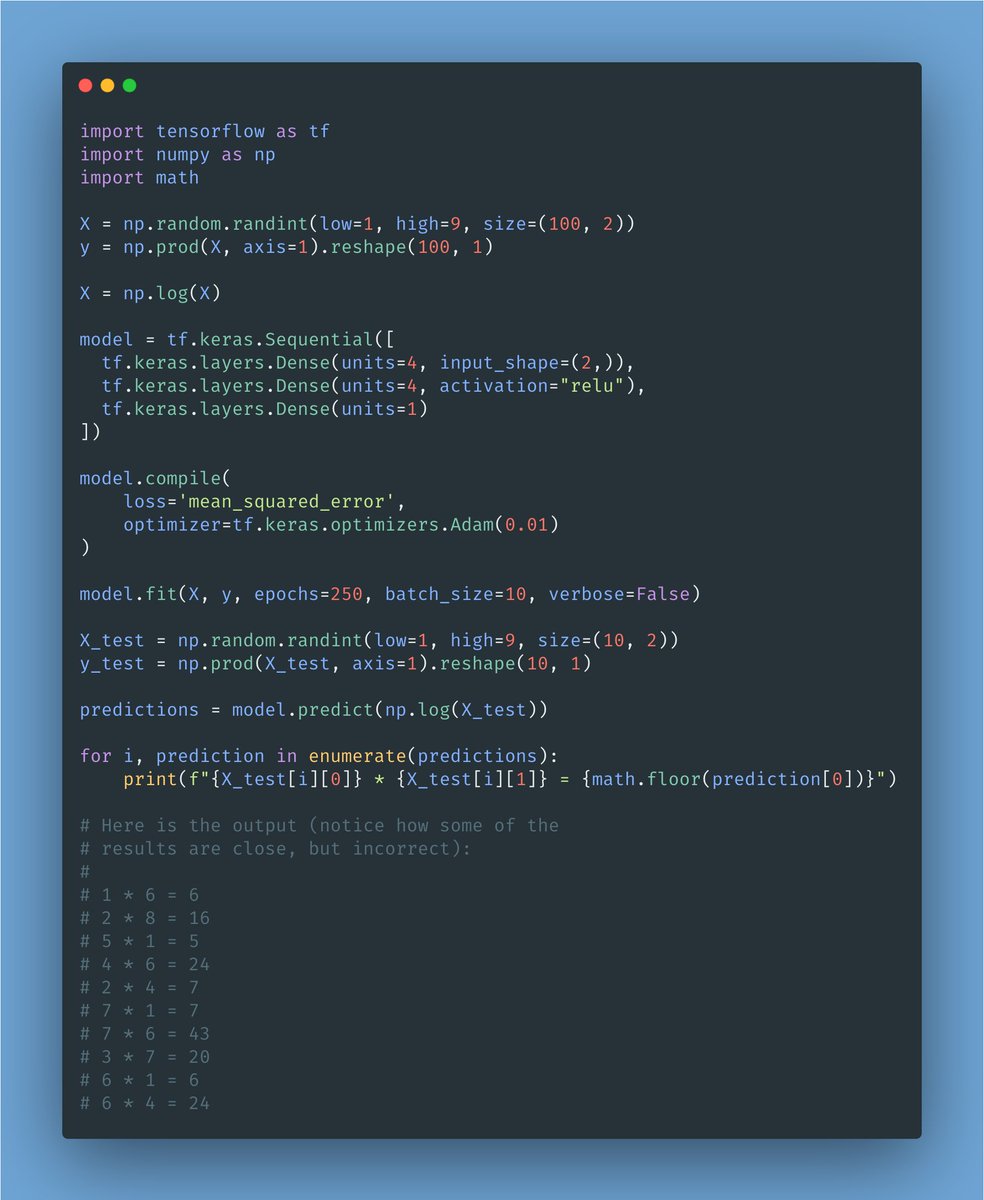
The goal of this model is to learn to multiply one-digit numbers.
https://twitter.com/freddyrojascama/status/1356251052190937089?s=20
The dataset has two values (the ones we want to multiply.) That's why the input shape is 2D.
The input shape represents the input layer of our model. It connects to the first hidden layer: a 4-unit Dense layer.
Then you get another 4-unit Dense layer.
The input shape represents the input layer of our model. It connects to the first hidden layer: a 4-unit Dense layer.
Then you get another 4-unit Dense layer.
https://twitter.com/Ivan94702842/status/1356346044657905667?s=20
Since we are dealing with large values (input numbers and the result of their multiplication,) normalizing them avoids the gradients to go out of whack.
That's what the "log" is for: it makes those values smaller and closer to each other.
That's what the "log" is for: it makes those values smaller and closer to each other.
https://twitter.com/bendowdell87/status/1356451233314275329?s=20
• • •
Missing some Tweet in this thread? You can try to
force a refresh






