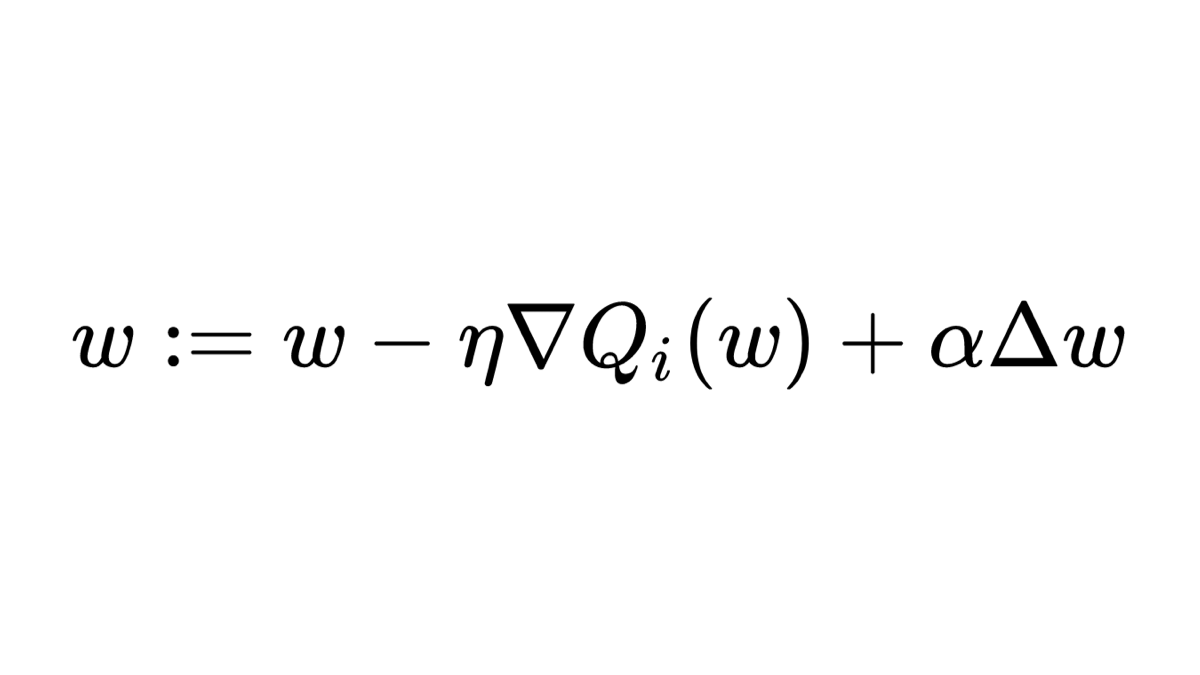Machine Learning Formulas Explained 👨🏫
This is the formula for Mean Squared Error (MSE) as defined in WikiPedia. It represents a very simple concept, but may not be easy to read if you are just starting with ML.
Read below and it will be a piece of cake! 🍰
Thread 👇
This is the formula for Mean Squared Error (MSE) as defined in WikiPedia. It represents a very simple concept, but may not be easy to read if you are just starting with ML.
Read below and it will be a piece of cake! 🍰
Thread 👇
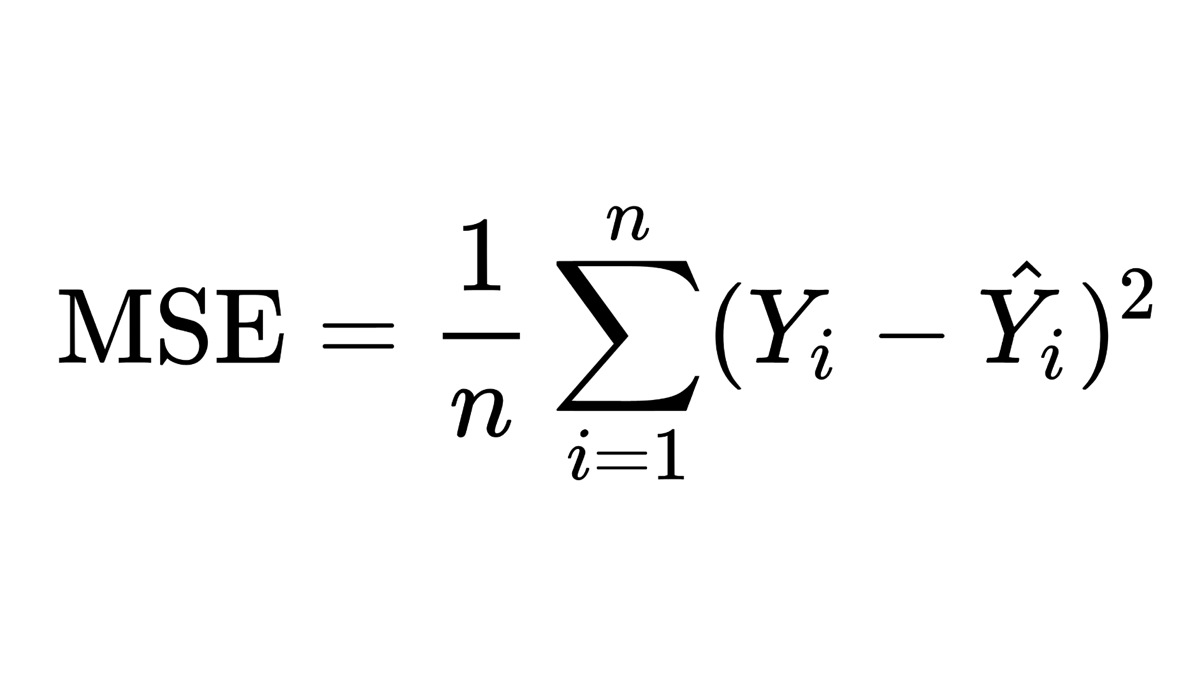
The core ⚫
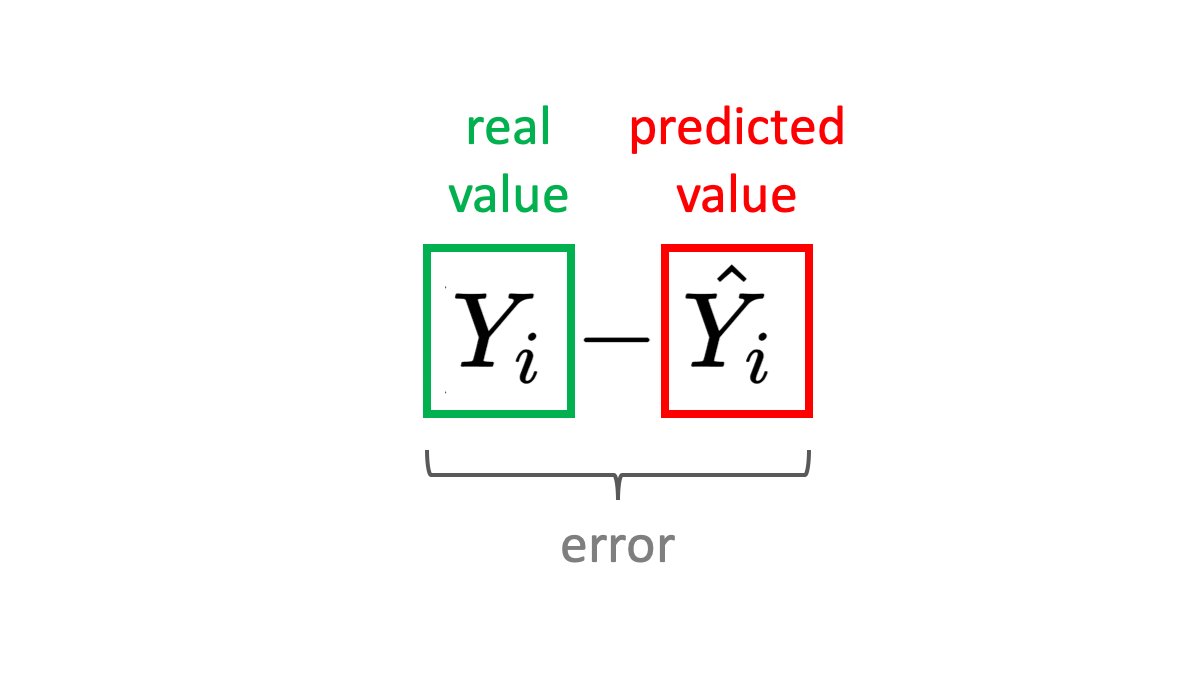
Let's unpack from the inside out. MSE calculates how close are your model's predictions Ŷ to the ground truth labels Y. You want the error to go to 0.
If you are predicting house prices, the error could be the difference between the predicted and the actual price.
Let's unpack from the inside out. MSE calculates how close are your model's predictions Ŷ to the ground truth labels Y. You want the error to go to 0.
If you are predicting house prices, the error could be the difference between the predicted and the actual price.
Why squared? 2️⃣
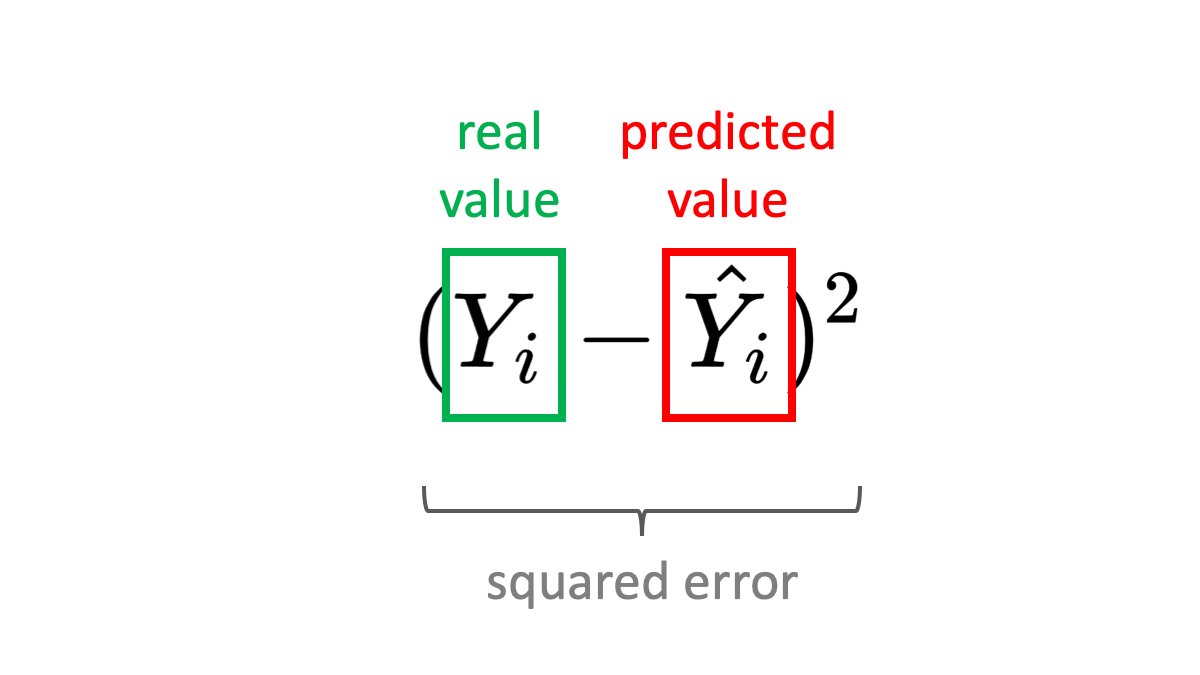
Subtracting the prediction from the label won't work. The error may be negative or positive, which is a problem when summing up samples.
You can take the absolute value or the square of the error. The square has the property that it punished bigger errors more.
Subtracting the prediction from the label won't work. The error may be negative or positive, which is a problem when summing up samples.
You can take the absolute value or the square of the error. The square has the property that it punished bigger errors more.
Why squared? Example 2️⃣
Imagine your pediction for the price of two houses is like this:
🏡 House 1: actual 120K, predicted 100K -> error 20K
🏠 House 2: actual 60K, predicted 80K -> error -20K
If you sum these up the error will be 0, which is obviously wrong...
Imagine your pediction for the price of two houses is like this:
🏡 House 1: actual 120K, predicted 100K -> error 20K
🏠 House 2: actual 60K, predicted 80K -> error -20K
If you sum these up the error will be 0, which is obviously wrong...
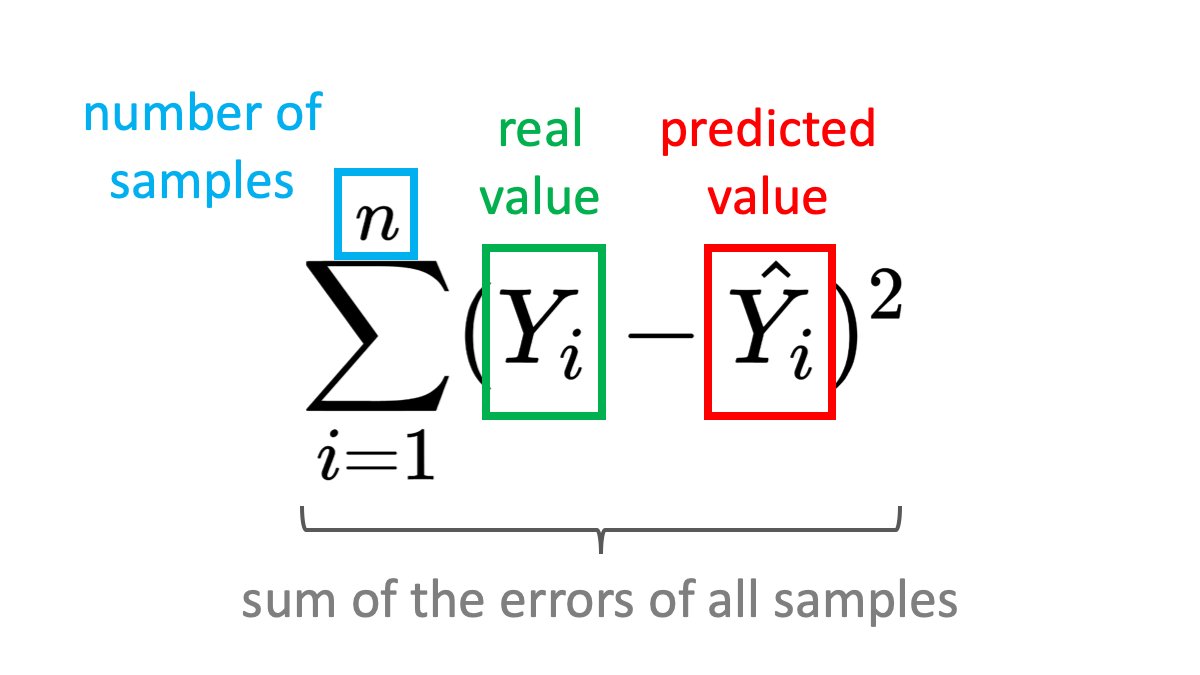
Summing up all samples ➕
When training your model you will have many samples (n) in your batch. We need to calculate the error for each one and sum it up.
Again, having the error be always ≥ 0 is important here.
When training your model you will have many samples (n) in your batch. We need to calculate the error for each one and sum it up.
Again, having the error be always ≥ 0 is important here.
Taking the average ➗
You are good to go how!
However, if you want to compare the errors of batches of different sizes, you need to normalize for the number of samples - you take the average.
For example, you may want to see which batch size produces a lower error.
You are good to go how!
However, if you want to compare the errors of batches of different sizes, you need to normalize for the number of samples - you take the average.
For example, you may want to see which batch size produces a lower error.

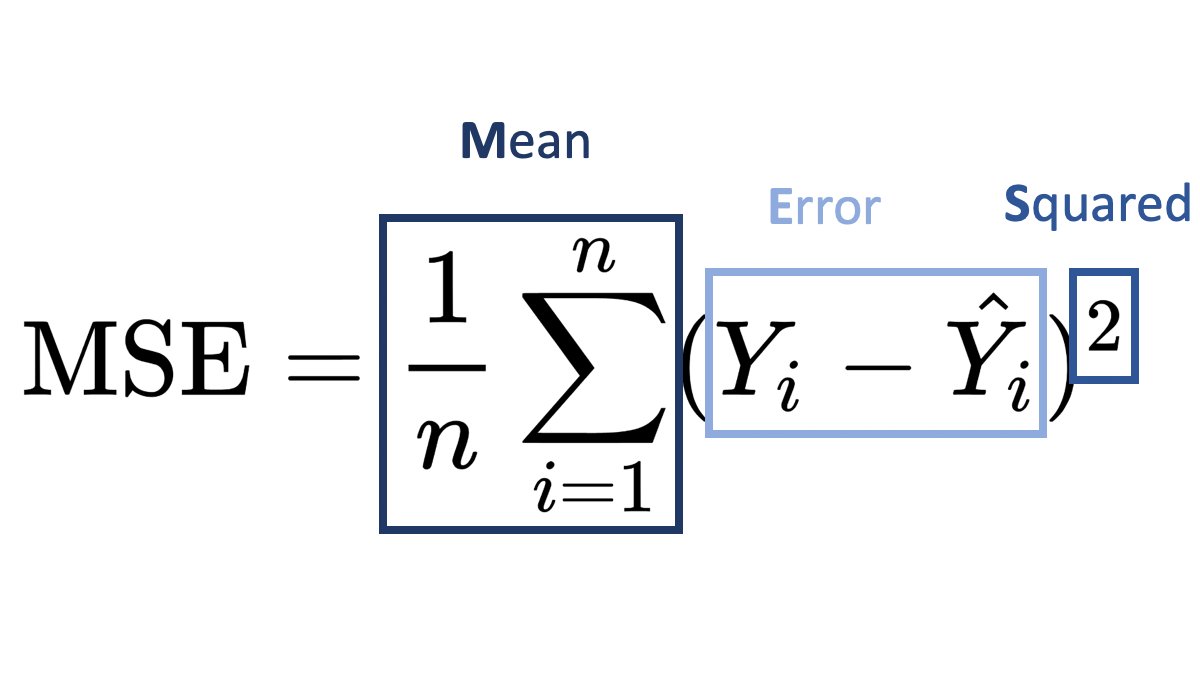
Mean Squared Error 📉
Now it should be easier to understand the formula!
MSE is a commonly used statistical measure and loss function in ML regression models (e.g. linear regression).
You should look into the Mean Absolute Error (MAE) as well, which handles outliers better.
Now it should be easier to understand the formula!
MSE is a commonly used statistical measure and loss function in ML regression models (e.g. linear regression).
You should look into the Mean Absolute Error (MAE) as well, which handles outliers better.
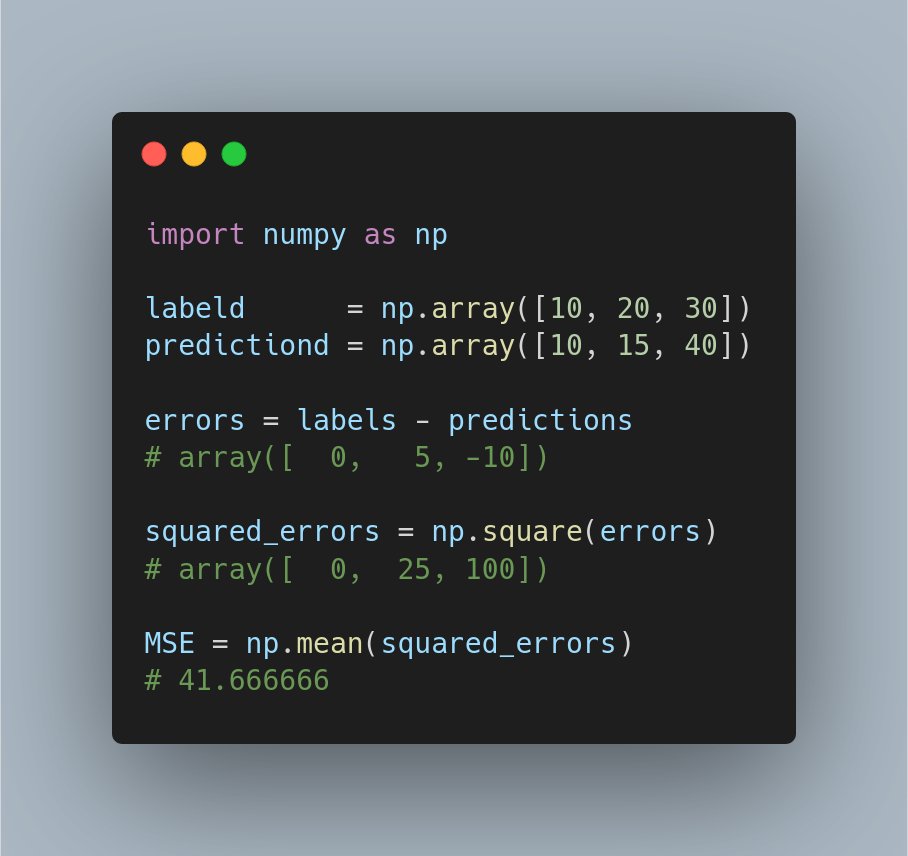
For the people that can "think" better in code, here a small Python example for calculating the Mean Square Error. 👨💻
Thanks to @ArpJann for the idea!
Thanks to @ArpJann for the idea!
• • •
Missing some Tweet in this thread? You can try to
force a refresh