Thread by @fkucuker__

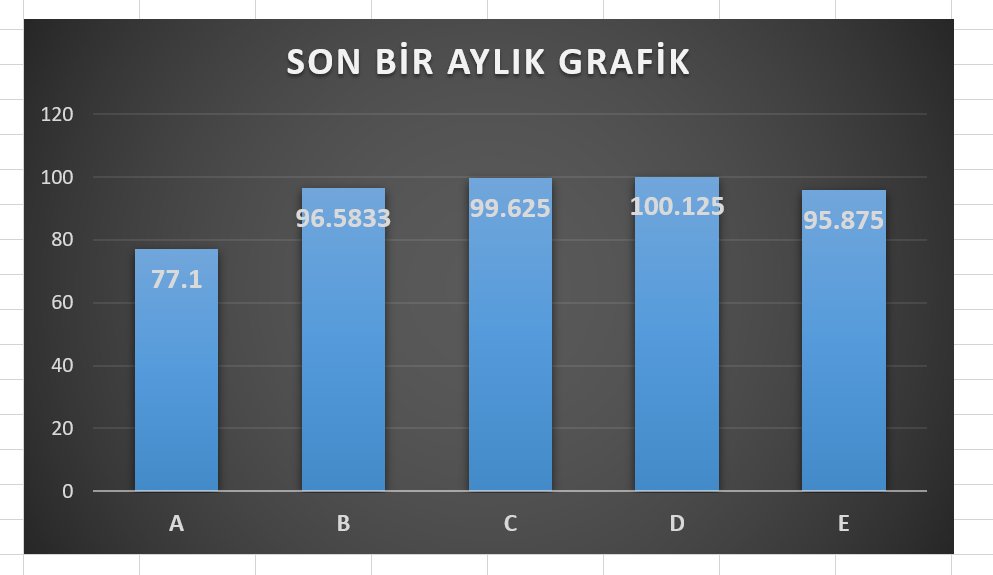
Bugün algoritmik trade’e yeni başlayanlar için korelasyon ve algotrading ilişkisi hakkında ufak bir bilgisel (flood ) yapacağım. Umarım arkadaşlar için faydalı olur.

Farkındaysanız #PARADISE ‘ın sahneye çıkması ile birlikte farklı karakterlere sahip sistemleri hızlı şekilde üretebilmeye başladık. Ancak piyasa hiçte küçümsenecek bir yapıya sahip olmadığından ekmek yine de aslanın ağzında gibi hissediyoruz. Paralar tıkır tıkır hesaba akmıyor.

Takip ettiğimiz hocaların hesaplarından sürekli sistemlerimizi çeşitlendirmemiz gerektiği uyarıları geliyor. Kimi zaman işlem sayılarını, kimi zaman MaxDD tarihlerini, kimi zamansa devreye girdikleri karakteristik yapıları çeşitlendirmemiz gerektiğini belirtiyorlar.

Peki tamam çeşitlendirelim ama nasıl? Çeşitlendirme ile kasıt edilen nedir? Çeşitlendirme yaparken sadece işlem sayılarını çeşitlendirmek yeterli midir? Ya da MaxDD ler birbirinden uzakta ise bu çeşitlendirme mi olmuştur?

Kısacası çeşitlendirme yapıp yapmadığımı nasıl anlayacağım? İşte bunların tamamının cevabı korelasyonlarda gizli…

Kısaca bu bilgiselle, korelasyon nedir? , korelasyon katsayısı nasıl hesaplanır, korelasyon matrisi nasıl oluşturulur ve sonuçları nasıl yorumlanır? Bunları açıklamaya çalışacağım.

Bunları Python, C#, MatLab gibi yazılımlar aracılığı ile de zorlanmadan yapabilirsiniz ancak ben basit ve ulaşılabilir olması açısından excel üzerinde izah etmeye çalışacağım.

Excel'de yapabileceğiniz en basit istatistiksel hesaplamalardan biri korelasyondur. Basit olmasına rağmen, iki veya daha fazla değişken arasındaki ilişkileri anlamada çok kullanışlıdır.

Korelasyon, iki değişken arasındaki ilişkinin gücünü ve yönünü tanımlayan bir ölçüdür. Genellikle istatistik, ekonomi ve sosyal bilimlerde bütçeler, iş planları ve benzeri işler için kullanılır.

Değişkenlerin ne kadar yakından ilişkili olduğunu incelemek için kullanılan yönteme ise korelasyon analizi denir.

Kavramların biraz daha kafamızda oturabilmesi için birkaç güçlü korelasyon örneği ile size yardımcı olayım.

➕ Yediğiniz kalori sayısı ve kilonuz (pozitif korelasyon)
➖Dışarıdaki sıcaklık ve ısıtma faturalarınız (negatif korelasyon)

Birkaç tane de zayıf korelasyon örneği verelim:

Kedinizin adı ve en sevdiği yiyecek

Gözlerinizin rengi ve boyunuz

Korelasyon hakkında anlaşılması gereken önemli bir şey, yalnızca iki değişkenin ne kadar yakından ilişkili olduğunu göstermesidir. Ancak korelasyon, nedensellik anlamına gelmez.

Bir değişkendeki değişikliklerin diğer değişkendeki değişikliklerle ilişkili olması gerçeği, bir değişkenin aslında diğerinin değişmesine neden olduğu anlamına gelmez.

Yani sizin 1 numaralı sisteminiz 2 numaralı sisteminiz ile körele ise 2 numara 1 numara kayıp yaşadığı için kayıp yaşamaz 1 ve 2 nolu sistemler birbirlerine çok benzedikleri için beraber kayıp yaşarlar.

İki sürekli değişken arasındaki ilişki derecesinin sayısal ölçüsü, korelasyon katsayısı (r) olarak adlandırılır. Katsayı değeri her zaman -1 ile 1 arasındadır ve değişkenler arasındaki doğrusal ilişkinin hem gücünü hem de yönünü ölçer.

Katsayının mutlak değeri ne kadar büyükse, ilişki o kadar güçlüdür:

-1 ve 1'in uç değerleri, tüm veri noktaları bir çizgiye düştüğünde mükemmel bir doğrusal ilişkiyi gösterir. Pratikte, olumlu ya da olumsuz mükemmel bir korelasyon nadiren gözlemlenir.

0 katsayısı, değişkenler arasında doğrusal bir ilişki olmadığını gösterir. İki dizi rastgele sayı ile elde etme olasılığınız tam olarak budur.

0 ile + 1 / -1 arasındaki değerler zayıf, orta ve güçlü ilişkilerin bir ölçeğini temsil eder. R değeri -1 veya 1'e yaklaştıkça, ilişkinin gücü artar.

Katsayı işaretinin artı veya eksi olması ilişkinin yönünü gösterir.

Pozitif katsayılar, doğrudan korelasyonu temsil eder ve bir grafikte yukarı doğru bir eğim oluşturur - bir değişken arttıkça diğeri de artar ve bunun tersi de geçerlidir.

Negatif katsayılar, ters korelasyonu temsil eder ve bir grafikte aşağı doğru bir eğim oluşturur - bir değişken arttıkça, diğer değişken azalmaya meyillidir.

Daha iyi anlamak için aşağıdaki korelasyon grafiklerine bakabilirsiniz.

1 katsayısı mükemmel bir pozitif ilişki anlamına gelir - bir değişken arttıkça diğeri orantılı olarak artar.

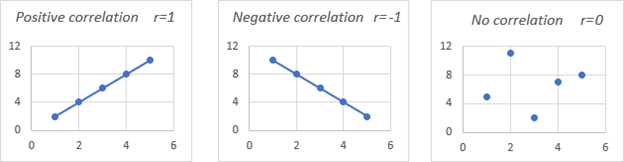
-1 katsayısı, mükemmel bir negatif ilişki anlamına gelir -bir değişken arttıkça diğeri orantılı olarak azalır.

0 katsayısı, iki değişken arasında ilişki olmadığı anlamına gelir - veri noktaları grafiğin her tarafına dağılmıştır.

Peki bu ilişkiler bizim algolarımız ile nasıl ilişkilendirilebilir ? VIOP içerisinde kar etmek için küçük yada büyük bir yöne doğru hareketin olması beklenir. Bu hareketler oluştukça kar edilir. Dolayısı ile geliştirilen sistemlerin birbirine uzak korele olma imkanları yoktur.

Ancak bir sistemin tüm hareketleri algılayıp alması imkansızdır. Bunu ancak sistemler topluluğu yapabilir (Bileşik Sistem), aynı zamanda bir sistemin sürekli kazanabilme şansıda yoktur. Bu piyasa da birilerinin para kazanabilmesi için birilerinin para kaybetmesi gerekir.

Bizlerin ise sistemleri geliştirirken yapmaya çalıştığı şey kaybederken az kaybetmek kazanırken ise mümkün olduğunca çok kazanmaktır.

Bunları yaparken geliştirdiğimiz sistemler birbirinden farklı zamanlarda en yüksek kazançlarını elde edip (bir sistemin tüm kazançları yakalayamayacağı kabulü ile), arklı zamanlarda en yüksek kayıplara maruz kalırsa. Ortalama kazanç eğimi her zamankinden daha stabil olacaktır.

Stabil kazanç eğrisi sizin zaman içerisinde sisteminize olan inancınızı artıracak, sizlere kazançlarınızı sermayeye ilave etme cesareti verecektir.

Tekrar konumuza dönelim, Pearson Korelasyonu korelasyon formülleri arasında en yaygın olarak kullanılanıdır. Her ne kadar buraya formülünü bırakacak olsam da sizleri çok fazla detay ile boğmayacağım. Çünkü excel’de bu korelasyon’a ulaşmak bir tık kadar kolay olacaktır.

KORELASYON komutu iki değer kümesi için Pearson korelasyon katsayısını döndürür. Sözdizimi çok kolay ve anlaşılırdır:

Aşağıdaki komut B42 ‘den O42’ ye kadar giden 1 nolu sistem ile , B43’den O43’e kadar giden 2 nolu sistem arasındaki korelasyon katsayısının ( R ) 0.99377 olduğunu bize vermektedir.

Söz konusu korelasyon sistemi 6 sistem içinde oluşturulduğu takdirde elde edilecek sonuca korelasyon matrisi adı verilir. Bu korelasyon ay ay , hafta hafta ve hatta gün, gün olacak şekilde yapılırsa, daha fazla bilgi elde edileceği için korelatif ayrışma daha ne gözükecektir.

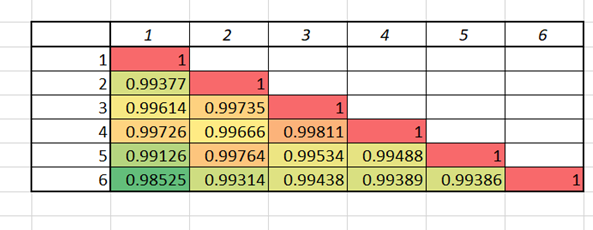
Ayrıca bu çalışma aynı sık süreler için MaxDD ve T.İşlem adetleri içinde yapılırsa hangi sistemin birbirinden ne kadar farklı olduğu daha net şekilde ortaya çıkacaktır.

Unutmayalım biz bileşik sistem oluştururken, adeta bir spor takımı oluşturuyoruz. Bir sistemin açığını diğerinin kapatmasını sağlıyoruz. Herkesin Ronaldo yada Messi olmasına gerek yok hatta 11 tane Ronaldo takıma zarar verebilir.

1 tane Ronaldo, 1 tane Atiba, 1 tane Muslera, 1 tane Mesut lazım bize… Tabloda yer alan değerler ise onların özellikleri. Herkese bol kazançlar...

Peki bu kadar korelasyon çalışmasının sonucu ne oldu, ne elde ettin diyen soranlar varsa da, bu sistemle devam etmeye karar verdim. Yine de hocaların yorumlarına açığım.