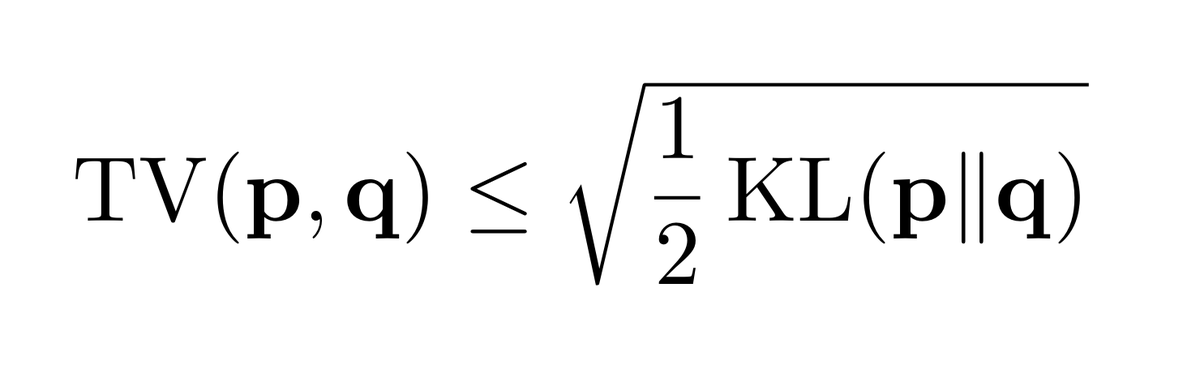Thread by @ccanonne_

📊 Answers and discussions for this week's thread on distinguishing biased coins 🪙. Coin: it's like a die 🎲, but with two sides.

So the goal is, given a 🪙, to distinguish b/w it landing Heads w/ probability p or >p+ε, with as few flips as possible.

https://twitter.com/ccanonne_/status/1374909562470297603

1/

Here, p and ε are known parameters (inputs), the goal is to be correct with probability at least 99/100 (over the random coin flips). As we will see, 99/100 is sort of arbitrary, any constant in 1/2 < c < 1 would work.

Also, warning: I'm going to give DETAILS.

2/

Let's start with Q1, the "fair" vs. ε-biased coin setting (p=1/2). As more than 66% of you answered, for Q1. the number of coin flips necessary and sufficient is then Θ(1/ε²). Why?

One way to think about it to gain intuition is "signal to noise."

3/

https://twitter.com/ccanonne_/status/1374909565020512263

If you take n coin 🪙 flips, the expectation of the number of Heads you see is either n/2 or n(1/2+ε). So the gap b/w the two is Δ=nε.
The *variance* of that number is np(1-p)=n/4 or n(1/4-ε²)≈n/4. So the standard deviation in both cases is σ≈√n/2.

Now, things will...

4/

.. typically fluctuate around their expectation by a few stds, so to be able to distinguish b/w the two cases we expect (!) to need Δ >> σ, that is nε >> √n. Reorganise, and you get n >> 1/ε².

Here's the intuition: let's make it formal! For the upper bound, the algorithm...
5/

... just follows the above. Count the number of Tails 🪙, threshold at T=n/4+Δ/2. To prove it works, use Chebyshev's inequality to get what the above argument states: if n >> 1/ε², the std is small compared to the gap Δ, and that thresholding works w/ high probability. Done!

6/

For the lower bound... Well, I have 3 options for you. All start by the standard fact that, given *one* sample from either P or Q one cannot distinguish b/w two distributions P,Q w/ proba of success greater than TV(P,Q) (up to some csts).

See e.g., math.stackexchange.com/questions/7272…

7/

Since n i.i.d. coin 🪙 flips from a Bernoulli P correspond to *one* sample from the product distribution Pⁿ (over {0,1}ⁿ), to distinguish we need the # of coin flips n to satisfy

TV(Pⁿ,Qⁿ) > 49/50

(don't focus on the constant) where P=Bern(1/2) and Q=Bern(1/2+ε).

8/

So our new goal: upper bound TV(Pⁿ,Qⁿ). A first idea 💡 is to use subadditivity of TV for product distributions:
TV(Pⁿ,Qⁿ) ≤ n TV(P,Q)
and since TV(P,Q)=ε (easy here, Bernoullis) we get (ignoring some constants) the lower bound n > 1/ε. That's... not great, we want 1/ε².
9/

💡Second attempt: subadditivity of TV distance is not tight, that's a well-known issue with TV. Let's use something else as a proxy, which plays well (technically, "tensorize").

Hell, let's do Hellinger distance: that's H(P,Q)=(1/√2)‖√P-√Q‖₂, which is weird but why not.
10/

Basically the ℓ₂ distance b/w square roots of the probability mass functions (TV was ℓ₁ b/w the pmfs). We conveniently know that TV(P,Q) ≲ H(P,Q), and that the *squared* Hellinger is subadditive*

*actually, even a bit better: we have an exact expression, but whatever.

11/

So we need the # n of 🪙 flips to satisfy

1 ≲ TV(Pⁿ,Qⁿ)² ≲ H(Pⁿ,Qⁿ)² ≤ n H(P,Q)² = Θ(nε²)

using that H(P,Q)² = ε²/2+o(ε²) (a simple computation, try it at home! wolframalpha.com/input/?i=Serie…)

Which gives our n = Ω(1/ε²) lower bound. 🥂

12/

💡Second option: you don't want to go to Hell(inger), you're more of an information-theorist. So... Kullback–Leibler divergence! Which is (sub)additive for product distributions: go tensorization! 🎊

KL(P₁⊗P₂,Q₁⊗Q₂)=KL(P₁,Q₁)+KL(P₂,Q₂)

13/

So we do the same thing and use Pinsker's inequality:

1 ≲ TV(Pⁿ,Qⁿ)² ≲ KL(Pⁿ,Qⁿ) ≤ n KL(P,Q) = Θ(nε²)

using that KL(P,Q) = 2ε²+o(ε²) – again a relatively simple computation for the KL b/w two Bernoullis: wolframalpha.com/input/?i=Serie…)

Again our n = Ω(1/ε²) lower bound. 🥂
14/

Last method: let's forget proxies and keep TV. Since, by the data processing inequality, TV distance can only go up by post-processing, the TV b/w the distributions of the *sum* of the n coin 🪙 flips is at least the TV b/w the distributions of the *tuples* of n flips. So..?

15/

The latter is TV(Pⁿ,Qⁿ), but the former is the TV b/w two binomials! So we get

1 ≲ TV(Pⁿ,Qⁿ) ≲ TV(Bin(n,1/2), Bin(n,1/2+ε))

At this point, you pray the TV distance b/w Binomials is known or you use some Gaussian 🔔 or Poisson 🐟 approximation and hope for the best.

16/

Good thing: it *is* know that

TV(Bin(n,1/2), Bin(n,1/2+ε)) ≍ ε√n

in our regime* and so we're good! Again, we get our n = Ω(1/ε²) lower bound. 🥂

* See for instance (2.15) and (2.16) in this paper of Adell and Jodrá: link.springer.com/article/10.115…
17/

So we have our upper and matching sample complexity lower bounds, Θ(1/ε²), and hopefully a bit of intuition about why it holds. That was the first question.

Yep, we still have 3 more to go! (It'll go faster though, I swear.)

18/

Q2 asked about an extremely biased coin: either always Tails, or *almost* always Tails. Here too, roughly 66% of you got the right answer: now Θ(1/ε) 🪙 flips are necessary and sufficient to distinguish b/w the two cases.
The proof is much easier, too!

https://twitter.com/ccanonne_/status/1374911022142656513

19/

Think of it as a Geometric r.v. with parameter ε, for instance: you need roughly 1/ε to see even *one* Heads with decent probability. Unless then, nothing you can say!

(Conversely, as soon as you see a Heads, you know it's not the p=0 coin 🪙.)

20/
en.wikipedia.org/wiki/Geometric…

What about Q3, where neither of the two coins is "trivial"? What if we want to distinguish b/w a coin w/ parameter 10ε and one w/ parameter 11ε, and be correct 99% of the time?

This one is tricky, ≈21% of you selected the right answer: Θ(1/ε) flips.

21/

https://twitter.com/ccanonne_/status/1374911480936554498

To see why, let's... not answer the question. Instead, let's discuss the more general statement below:

Claim. To distinguish b/w a coin w/ parameter α and one w/ param α(1+β), Θ(1/(αβ²)) coin flips are necessary and sufficient.

This implies the above for α=10ε and β=1/10.

22/

Let's start with the upper bound: the same type of 𝔼+variance+Chebyshev analysis as in Q1 will do the trick. To see why, consider our signal-to-noise argument:
- the gap in 𝔼 b/w the 2 cases is Δ=nαβ
- the std in both cases (β<<1) is ≈√(nα).

We need nαβ >> √(nα), done.

23/

For the lower bound? Let's adapt our KL divergence proof. We again need

1 ≲ TV(Pⁿ,Qⁿ)² ≲ KL(Pⁿ,Qⁿ) ≤ n KL(P,Q)

and now KL(P,Q)=Θ(αβ²), so n must be Ω(1/(αβ²)) Hurray! 🥂

(for α,β→0 at least, this is "easy" to show: wolframalpha.com/input/?i=Serie…)

24/

But that's an argument, maybe we can have more intuition?

Think of it this way: with probability 2α, you get to toss a coin 🪙 which has parameter either 1/2, or (1+β)/2. But with probability 1-2α, you don't toss anything, you just get Tails.

In that thought experiment...

25/

You do get either (overall) a 🪙 with parameter either 2α×1/2=α, or 2α×(1+β)/2=α(1+β). But in that new setting it's clearer why we get Θ(1/(αβ²)): only every 1/α flips or so, you get *one* flip from the "useful" coin which is either biased or fair.

So we get (1/α)×Θ(1/β²)!

26/

Time to wrap up and handle the last, Q3: "this is all good, but what if 99% success probability isn't good enough for me, and instead I want 1-δ for arbitrarily small δ>0?"

Well, is *anything* ever good enough?

Then: 70% of you got it right! Just...

https://twitter.com/ccanonne_/status/1374913236420587521

27/

... multiply all the bounds we discussed by a factor log(1/δ), and you're good.

How so, you ask? The upper bound is quite fun and useful: suppose you have an algo taking n samples, and with success probability 99%.

Then set t=O(log(1/δ)), repeat that algo independently...

28/

... t times on indept samples (so tn=O(nlog(1/δ)) samples overall), and take a majority of the t outputs (which are just bits, since we're doing testing).

By Chernoff/Hoeffding, this gives the right answer w/ probability at least 1-δ: the success probability was "amplified."
29/

For the lower bound, now.. you remember our KL-based lower bound, on tweet #14 of the 🧵? We used Pinsker's inequality to relate TV to KL.

We can use another inequality instead, and we'll get the log(1/δ) in the lower bound "for free." 🤯

Cf. below+one line of algebra...

30/

... specifically noting that, reorganizing, we get
e^(-Θ(nε²)) ≤ 2δ-δ²
hence the final bound.

More on Pinsker vs. Bretagnolle–Huber:
🧵 This thread:

https://twitter.com/ccanonne_/status/1339333361777569792

📝This writeup: github.com/ccanonne/proba…

OK, that wraps it up I believe!

31/

I hope you enjoyed this week's quiz on 🪙, and the (admittedly, a bit long) discussion. Let me know below if you have any question, or comment, or feedback!

32/end