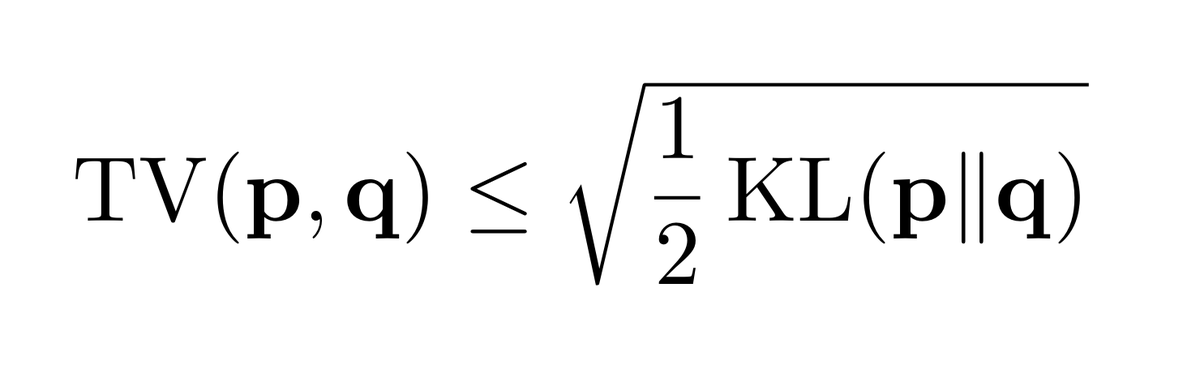Thread by @ccanonne_

Here is one:
If X has the same distribution as X', Y as Y', and Z as Z', do we have 𝔼[X+Y+Z]=𝔼[X'+Y'+Z']?

https://twitter.com/ccanonne_/status/1372702428110327808

Note that this is true for only two r.v.'s: if X~X' and Y~Y'
𝔼[X+Y]=𝔼[X'+Y']
whenever 𝔼[X+Y] is defined (regardless of whether 𝔼[X] and 𝔼[Y] are defined). (cf. below from G. Simons (1977)).

Turns out, this fails for 3 r.v.'s (same paper by Simons, and Counterexample 6.1 in Stoyanov's book).

Sometimes 𝔼[X+Y+Z], 𝔼[X'+Y'+Z'] both exist, yet 𝔼[X+Y+Z]≠𝔼[X'+Y'+Z'].

(Again, for 2 r.v.'s the result holds: if 𝔼[X+Y], 𝔼[X'+Y'] both exist, then 𝔼[X+Y]=𝔼[X'+Y'].)

Here is the paper in question, referenced in Stoyanov's book.

X,Y,Z are dependent and defined such that all three are marginally tan(πU/2) for U~Unif[0,1], but X+Y+Z=0. So 𝔼[X+Y+Z]=0.

X',Y',Z' have different dependence structure, but same marginals. 𝔼[X'+Y'+Z']=(4/π) log 2.

Specifically, take U~Unif[0,1], and set

X=Y=tan(πU/2), Z=-2X.
X'=tan(πU/2), Y'=tan(π(1-U)/2), Z'=-2tan(π|2U-1|/2).

"An Unexpected Expectation," indeed. Here is the paper: doi.org/10.1214/aop/11…