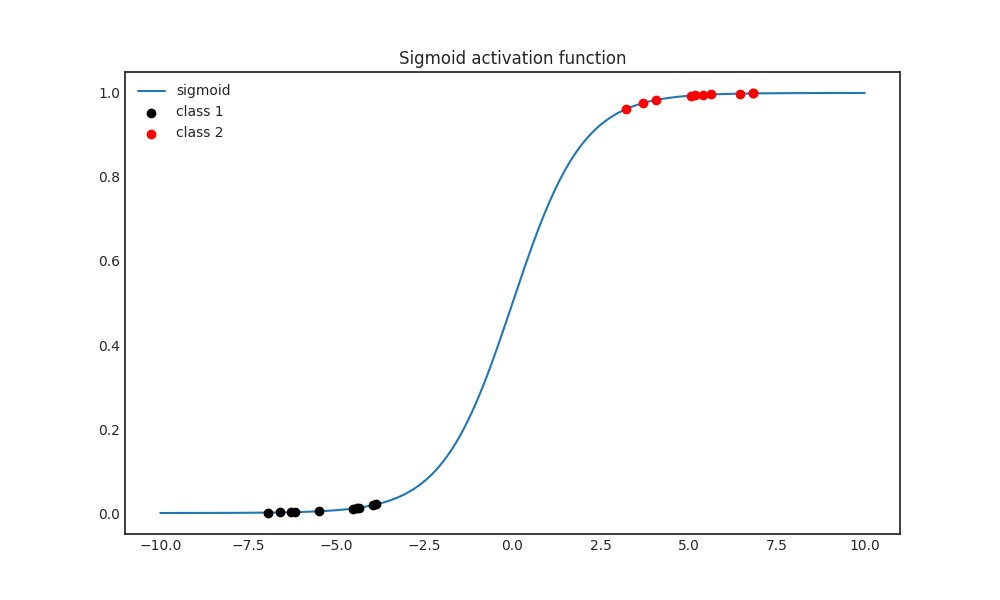
There is a common misconception that all probability distributions are like a Gaussian.
Often, the reasoning involves the Central Limit Theorem.
This is not exactly right: they resemble Gaussian only from a certain perspective.
🧵 👇🏽
Often, the reasoning involves the Central Limit Theorem.
This is not exactly right: they resemble Gaussian only from a certain perspective.
🧵 👇🏽
Let's state the CLT first. If we have 𝑋₁, 𝑋₂, ..., 𝑋ₙ independent and identically distributed random variables, their scaled sum is a Gaussian distribution in the limit.
The surprising thing here is the limit is independent of the variables' distribution.
The surprising thing here is the limit is independent of the variables' distribution.

Note that the random variables undergo a significant transformation: averaging and scaling with the mean, the variance, and √𝑛.
(The scaling transformation is the "certain perspective" I mentioned in the first tweet.)
(The scaling transformation is the "certain perspective" I mentioned in the first tweet.)
How can we unravel what this transformation means?
For this, we have to go back to the Law of Large Numbers, which states that the average converges to the expected value.
The Central Limit Theorem is essentially the speed of this convergence!
For this, we have to go back to the Law of Large Numbers, which states that the average converges to the expected value.
The Central Limit Theorem is essentially the speed of this convergence!
https://twitter.com/TivadarDanka/status/1362422719049007107
In general, if we have two sequences of numbers 𝑎ₙ and 𝑏ₙ, we can compare their magnitudes by taking the limit of their ratio.
When both 𝑎ₙ and 𝑏ₙ converges to 0, the existence of this limit implies that they have the same speed.
When both 𝑎ₙ and 𝑏ₙ converges to 0, the existence of this limit implies that they have the same speed.
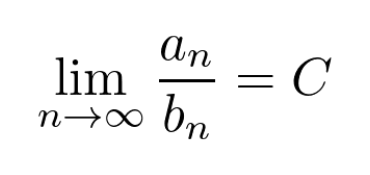
In the Central Limit Theorem, we essentially take the ratio of two such sequences, as you can see below. 

Since we are talking about random variables and not deterministic sequences, the situation is a bit more complicated.
In the Central Limit Theorem, the convergence is in distribution, not in a pointwise sense. (Keep in mind that random variables are functions.)
In the Central Limit Theorem, the convergence is in distribution, not in a pointwise sense. (Keep in mind that random variables are functions.)
The fact that the limiting distribution is a Gaussian means that we not only know the rate of convergence of the scaled averages, we also know how much it fluctuates around the sequence we compare it to.
(Which is 1/√𝑛.)
(Which is 1/√𝑛.)
To summarize, a real-life distribution only resembles a Gaussian if it is an average of independent measurements.
A good example is the winnings of a poker player, averaged per hand.
A good example is the winnings of a poker player, averaged per hand.
A famous, not Gaussian-like distribution is the Pareto distribution. This often captures the phenomenon where the vast majority of samples have low value and a minority is extremely high.
Wealth distribution and the number of Facebook friends both fall into this category.
Wealth distribution and the number of Facebook friends both fall into this category.
TL;DR: not all distributions are Gaussian. Only their properly scaled averages are, if they are independent and identically distributed with finite mean and variance.
• • •
Missing some Tweet in this thread? You can try to
force a refresh