*Weisfeiler and Lehman Go Topological*
Fantastic #ICLR2021 paper by @CristianBodnar @ffabffrasca @wangyg85 @kneppkatt Montúfar @pl219_Cambridge @mmbronstein
Graph networks are limited to pairwise interactions. How to include higher-order components?
Read more below 👇 /n
Fantastic #ICLR2021 paper by @CristianBodnar @ffabffrasca @wangyg85 @kneppkatt Montúfar @pl219_Cambridge @mmbronstein
Graph networks are limited to pairwise interactions. How to include higher-order components?
Read more below 👇 /n

The paper considers simplicial complexes, nice mathematical objects where having a certain component (e.g., a 3-way interaction in the graph) means also having all the lower level interactions (e.g., all pairwise interactions between the 3 objects). /n 
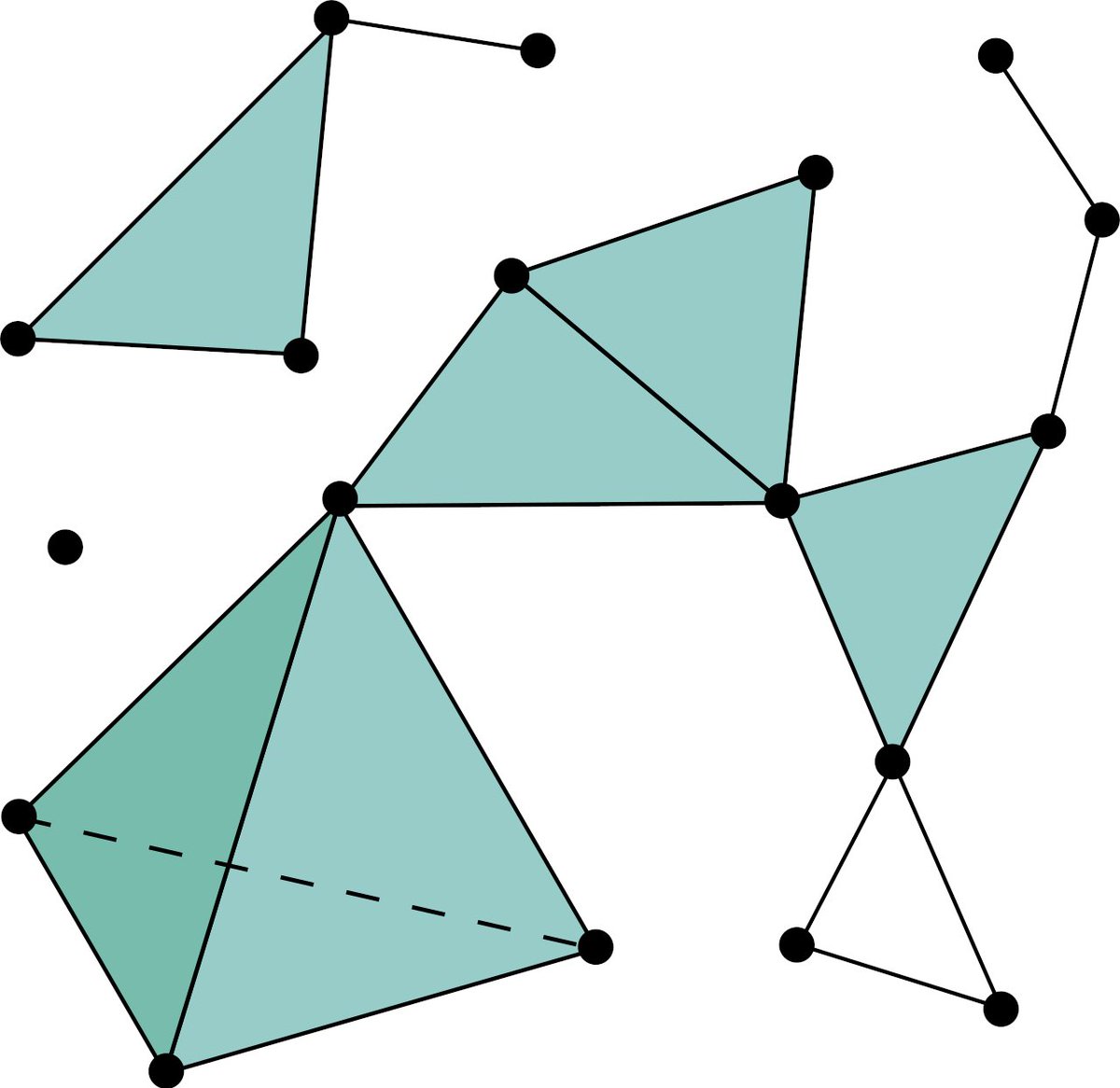
Simplicial complexes have many notions of "adjacency" (four in total), considering lower- and upper- interactions.
They first propose an extension of the Weisfeiler-Lehman test that includes all four of them, showing it is slightly more powerful than standard WL. /n
They first propose an extension of the Weisfeiler-Lehman test that includes all four of them, showing it is slightly more powerful than standard WL. /n

A message-passing network can be defined similarly, by using four different types of exchange functions.
They also show that two of them are redundant, making the final formulation have only linear scaling properties. /n
They also show that two of them are redundant, making the final formulation have only linear scaling properties. /n

They have many interesting experiments by building clique complexes from the original graph, showing MPSNs are better at discriminating graphs.
No public code yet, by it's apparently "coming soon"! 😎
Preprint is here: arxiv.org/abs/2103.03212
No public code yet, by it's apparently "coming soon"! 😎
Preprint is here: arxiv.org/abs/2103.03212

• • •
Missing some Tweet in this thread? You can try to
force a refresh