Thread by @mcnees

Astronomer Vera Rubin was born #OTD in 1928. Her work on galactic rotation curves became one of the main pieces of evidence for the existence of dark matter, and she deserved a Nobel Prize for it. #BirthdayVeraRubin
Image: Vassar College / Emilio Segrè Visual Archives

The modern case for dark matter began with Fritz Zwicky in the 1930s. His observations of galaxies in the Coma Cluster suggested there simply wasn't enough luminous matter present to gravitationally hold everything together. Hence, there must be matter there that you can't see.

Around that same time, a young Vera Rubin was looking up at the night sky in wonder, memorizing the paths of meteors and pondering the stars.

In interviews, she would often say “I just couldn’t look at the sky without wondering how anyone could do anything but study the stars.”

So Rubin studied astronomy at Vassar College, graduating in 1948. After that, she followed her husband to Cornell where she completed a Master's Degree in 1951.

For her Master's Thesis, Vera Rubin showed that some galaxies and clusters seemed to deviate from their local Hubble flow. This wasn't taken very seriously by her colleagues. In her words, it was "believed by very few astronomers."

After that, Rubin pursued her PhD at Georgetown, where she was supervised by George Gamow. She studied variations in the spatial distribution of galaxies – work that would explain the phenomena she had observed in her Master's Thesis.

No one knew it at the time, but Rubin had identified the Supergalactic Plane.

After completing her PhD in 1954, Rubin presented these results at the AAS meeting.

One advisor, William Shaw, offered to present the results for her, because she was pregnant. But only if he could present them in *his* name.
astronomy.com/news/2016/10/v…

Again, the work was not well-received. But Rubin was ahead of her time, and the investigation of large-scale structure would soon become one of the major themes of astronomy. See, for instance:

https://twitter.com/mcnees/status/1336336841889345537

Vera Rubin joined the faculty of the Carnegie Institute in 1964. In the early 1970s she began the work for which she is most famous: Optical spectra of spiral galaxies that extended far enough from the galactic nucleus to provide support for flat rotation curves. (@CarnegieAstro)

So what is a rotation curve, what does it mean to be "flat," and what does that have to do with dark matter?

Suppose you measure orbital velocities of stars and gas circling the center of a galaxy. If you know how matter is distributed throughout the galaxy, you can use plain old Newtonian gravity to get an idea of how fast things should be moving, and compare with your observations.

To keep things simple, imagine a spherical galaxy. According to Newton, a star at distance r from the center of the galaxy should orbit with speed that depends on r and the amount of galactic mass M(r) out to distance r. (G is Newton's constant, 6.67 x 10⁻¹¹ m³ kg⁻¹ s⁻².)

M(r) increases as you move out from the center of the galaxy. The density of luminous matter – stuff you can see – may look more or less constant out to r, in which case M(r) ~ r³. Then you would expect orbital speeds within the galaxy to grow linearly with r.

The galaxy has a finite size, so out past some distance R_{L} there is no more luminous matter and for r > R_{L} the mass M(r) no longer changes. Since it stays the same but r gets bigger, the ratio M(r)/r gets smaller and the orbital speed begins to fall off like v ~ √(1/r).

A "rotation curve" is a plot with orbital speed on the vertical axis and distance from the center of the galaxy on the horizontal. For the scenario I just described, you would expect it to look something like the plot below.

Now, most of the galaxies we observe are *not* spherical. But spiral galaxies should have a similar behavior: v increases as you move out from the center, then falls off when you're out past the luminous matter. Here's what Newtonian gravity gives for a disk-shaped galaxy:

The key is that once you're out past most of the luminous stuff – the matter that makes up what you think of as the galaxy – orbital speeds should start to fall off. In the simple case we started with this is called "Keplerian falloff."

So we expect to see this falloff in the orbital velocity of gas and other matter loitering out past the "edge" of the galaxy. But this isn't what Vera Rubin and her collaborators found!

Instead, Rubin et al measured rotation curves that became roughly *flat* out past the point where the density of luminous matter dropped off. And stuff at the edge of the galaxy was orbiting too fast given the matter they could account for.

The 1980 Astrophysical Journal paper by Rubin, Ford, and Thonnard is usually cited in textbooks discussing this phenomenon. Look at those rotation curves!
ui.adsabs.harvard.edu/abs/1980ApJ...…
Image: Astrophysical Journal, Vol. 238, p. 471-487 (1980)

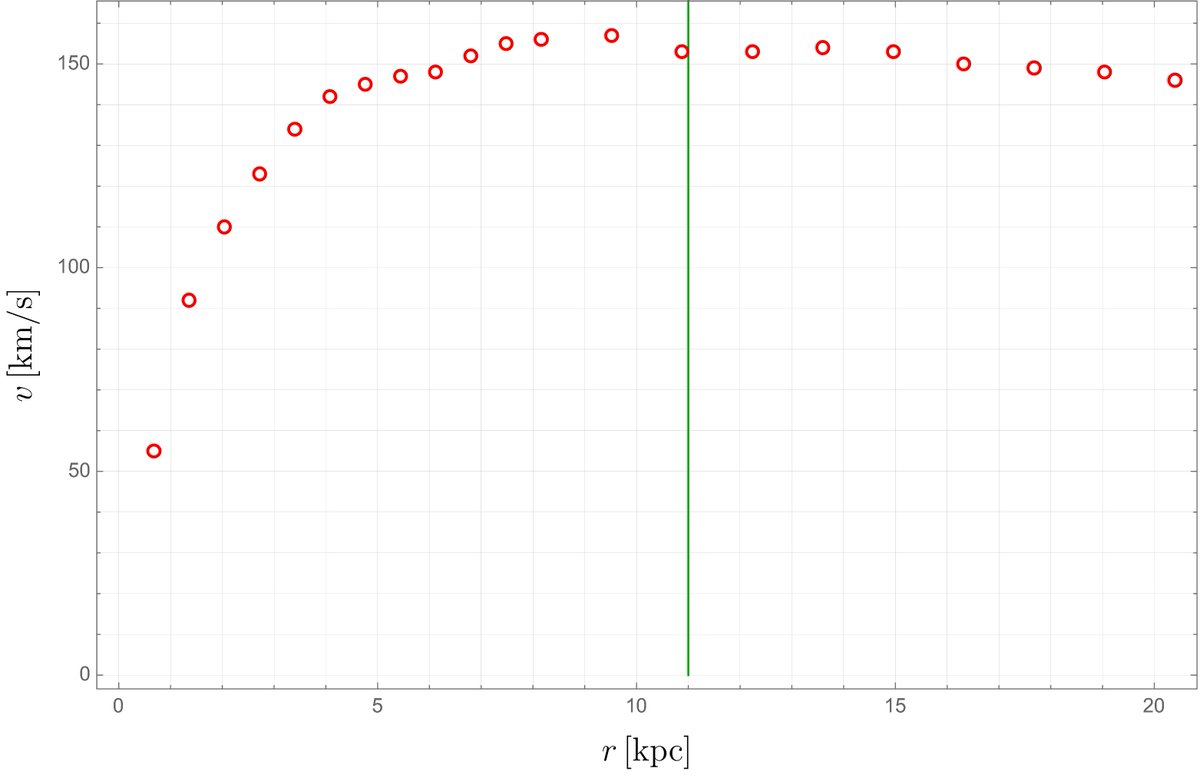
Here's a rotation curve for galaxy NGC 3198. The green vertical line is the approximate edge of the galaxy. As you can see, there's no significant falloff - the curve is flat.
Data: K. G. Begeman, “HI rotation curves of spiral galaxies,” PhD thesis, U Groningen (1987)
Image: NASA

There was already evidence for flat rotation curves from radio observations. Rubin et al took advantage of advances in optical instrumentation to provide unambiguous evidence of the disconnect between rotation rates and the amount of luminous matter in galaxies.

(More on that in a moment.)

So what's going on here? Why are the observations so different than our predictions? Maybe Newton's Law of Universal Gravitation, which was central to all our predictions in the previous tweets, is the problem. Could gravity work a little differently on these galactic scales?

That's a fine possibility to consider, but there's a pretty good body of evidence that suggests it's not the explanation. In all likelihood, Newton's description of gravity is perfectly valid here.

If Newton's Law isn't the problem, what is?

There's a very (conceptually) simple explanation. When we were working out that first rotation curve, we assumed that the mass M(r) out to distance r came from all the luminous stuff we could see. But what if there's other matter besides that?

Suppose the galaxy is surrounded by a large halo of non-luminous matter with density that falls off like 1/r² as you move out from the center. That would give another contribution to M(r) that is proportional to r.

If the non-luminous halo extends out further than the luminous matter, then this contribution to M(r) is still increasing out past what we previously called the "edge" of the galaxy. As a result, the orbital velocity levels off for r > R_{L}. The rotation curve flattens.

Once you add a non-luminous component like this to your description of the galaxy, Newtonian gravity does a pretty good job of explaining our orbital velocity measurements. Here's what we get for that NGC 3198 data.

Now, I am glossing over a lot of details here, but that's the main idea. You look at how fast things are moving as a function of distance from the galactic center. The amount of matter you can see doesn't provide enough of a gravitational tug to explain those observations.

To explain the data you need more matter, stuff we don't see via the electromagnetic interactions that allow us to detect the luminous stuff.

Non-luminous isn't a very catchy name, so we call it "Dark Matter."

The case for dark matter is very strong and extends well beyond galactic rotation curves. Dynamics of galaxy clusters, gravitational lensing, the existence of especially old galaxies, and cosmological models all support the existence of dark matter.

And dark matter seems to make up about 27% of the universe! This is perhaps surprising. The matter we are familiar with – the baryons and fermions of the current Standard Model of particle physics – is less than about 5% of the total energy budget of the Universe.

There's a pretty good list of folks who should share the credit for the discovery of dark matter. Long before Zwicky, Kelvin tried to survey the mass content of "dark bodies" in our galaxy. Poincaré introduced the term "matière obscure" when rebutting him.

Both Kapteyn and Oort suggested that there was too little visible matter to explain the dynamics of stars in our galaxy. Rubin and Ford's work took place throughout the 1970s; Albert Bosma's 1978 thesis provides radio measurements of flat rotation curves:
ned.ipac.caltech.edu/level5/March05…

Bosma himself wrote a detailed account of all the folks who he felt should receive more credit for their work establishing flat rotation curves. (H/t @AstroMikeMerri)
ned.ipac.caltech.edu/level5/Sept03/…

Imo the evidence for dark matter has always been just as solid as the evidence for dark energy, which earned a Nobel Prize in 2011. But the historically sexist Nobel Committee never recognized Rubin with a share of a prize for dark matter. They just waited until she passed away.

If helping discover roughly 27% of the Universe isn’t enough, what is? The lack of a Nobel doesn't diminish Rubin's contributions, but it did a lot to diminish my opinion of the Nobel.

Image: Carnegie Institution of Washington

You should read @IBJIYONGI’s @BitchMedia piece on Vera Rubin from a few years ago.
bitchmedia.org/article/vera-r…

Let me wrap up (for now) with David DeVorkin's interview with Vera Rubin for @AIP_HQ's oral history series. It's a great read.
aip.org/history-progra…

@AIP_HQ This bit, especially, does a beautiful job of capturing the germ of basic research. DeVorkin asks Rubin what possessed her as a child to stay up late and study the sky.

Rubin: “I don’t have the vaguest idea. I just found it fascinating.”

Happy birthday, Vera Rubin.

Take a few minutes to check out @VRubinObs's #BirthdayVeraRubin posts.