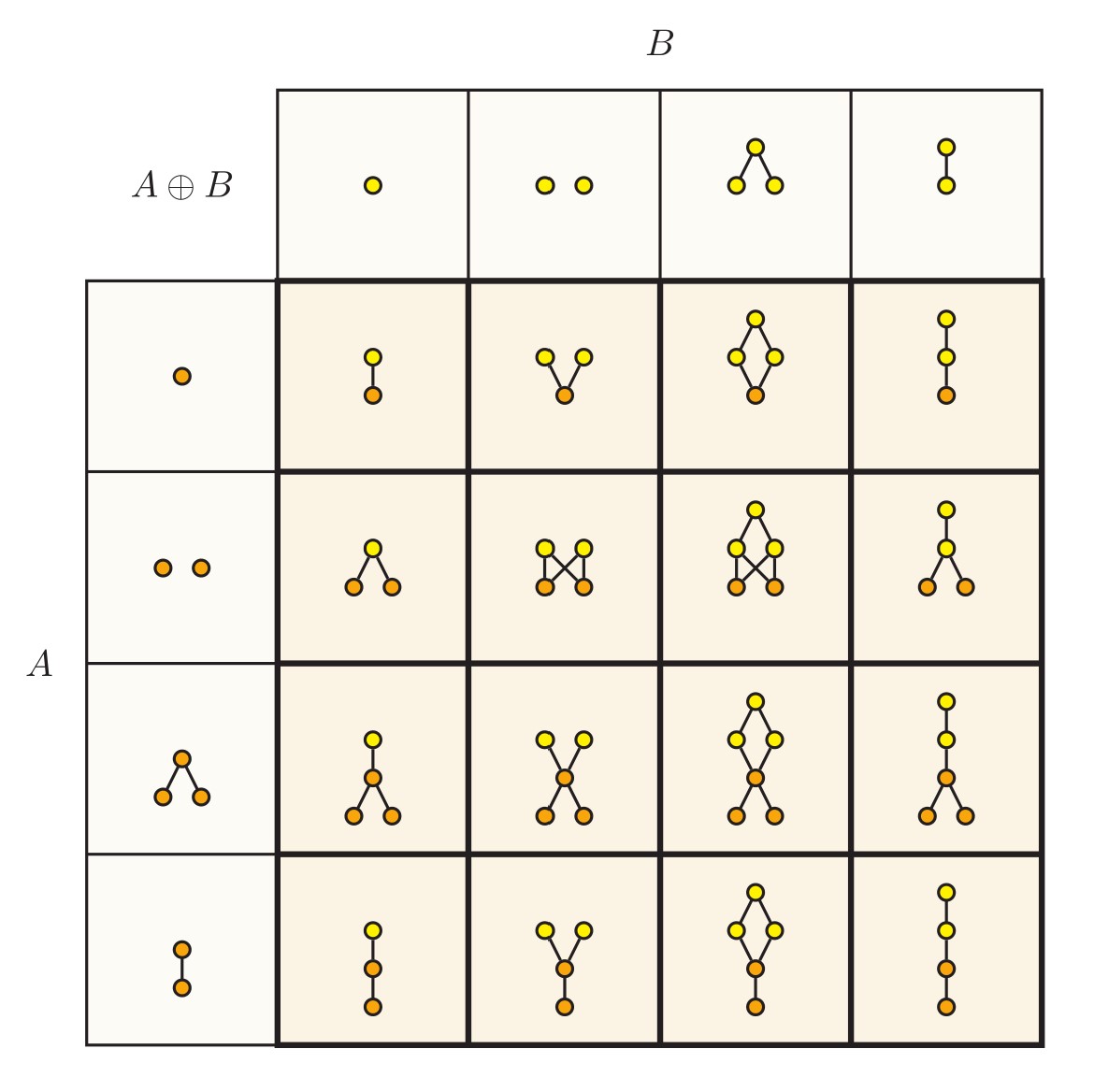
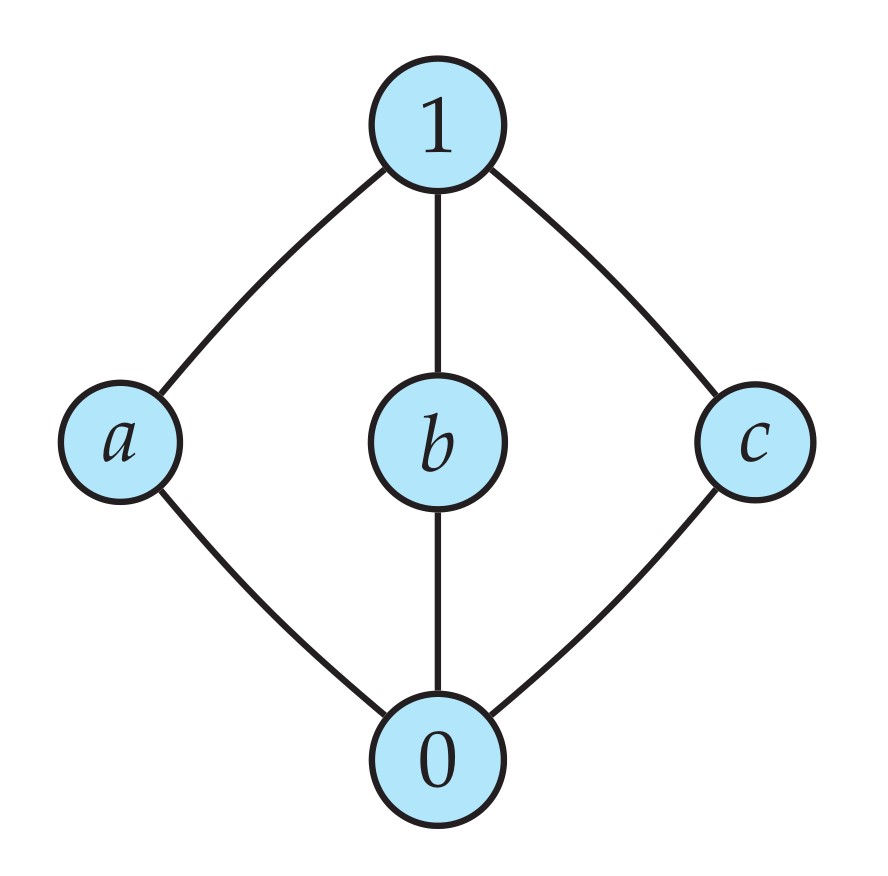
Order relations are often fruitfully conceived as being stratified into a linear hierarchy of levels. The simple order shown here, for example, is naturally stratified by three levels. 

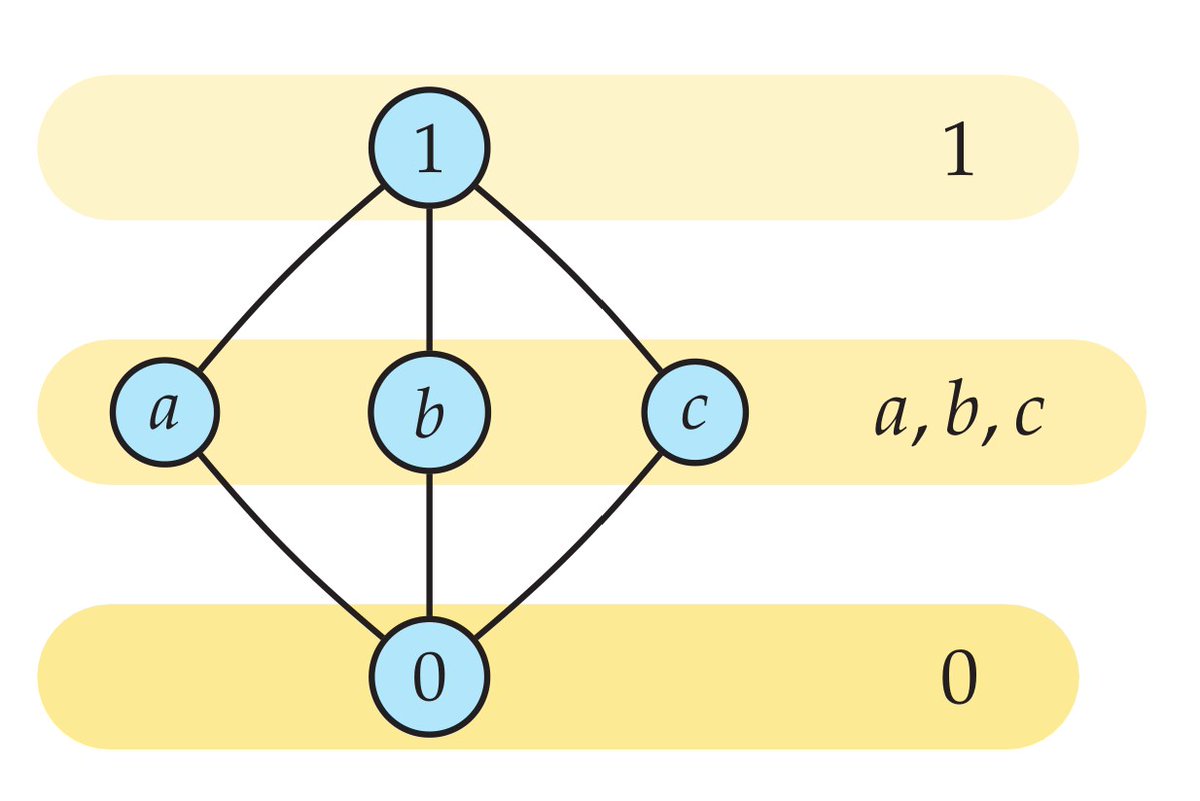
What is a "level"? A stratification of an order into levels amounts to a linear preorder relation on the same domain. namely, a linear grading of a partial order ≼ is a preorder relation ≤ respecting the strict relation, that is, for which a≺b implies a<b.
There are often far more linear gradings of a partial order than one might expect. The simple order shown in this post above, for example, admits thirteen distinct gradings! 

Meanwhile, every partial order admits some linear grading into levels. Indeed, every partial order is refined by a linear order, and so there is a grading of the order into levels placing exactly one node on each level.
I prove that theorem and provide further discussion in my blog post. jdh.hamkins.org/linear-grading…
And to clarify—I worry some people may have misunderstood—this post is an exposition of elementary material that I would consider to be part of a sound introduction to logic. This is a selection from my book-in-progress, Topics in Logic, from the section on orders.
• • •
Missing some Tweet in this thread? You can try to
force a refresh