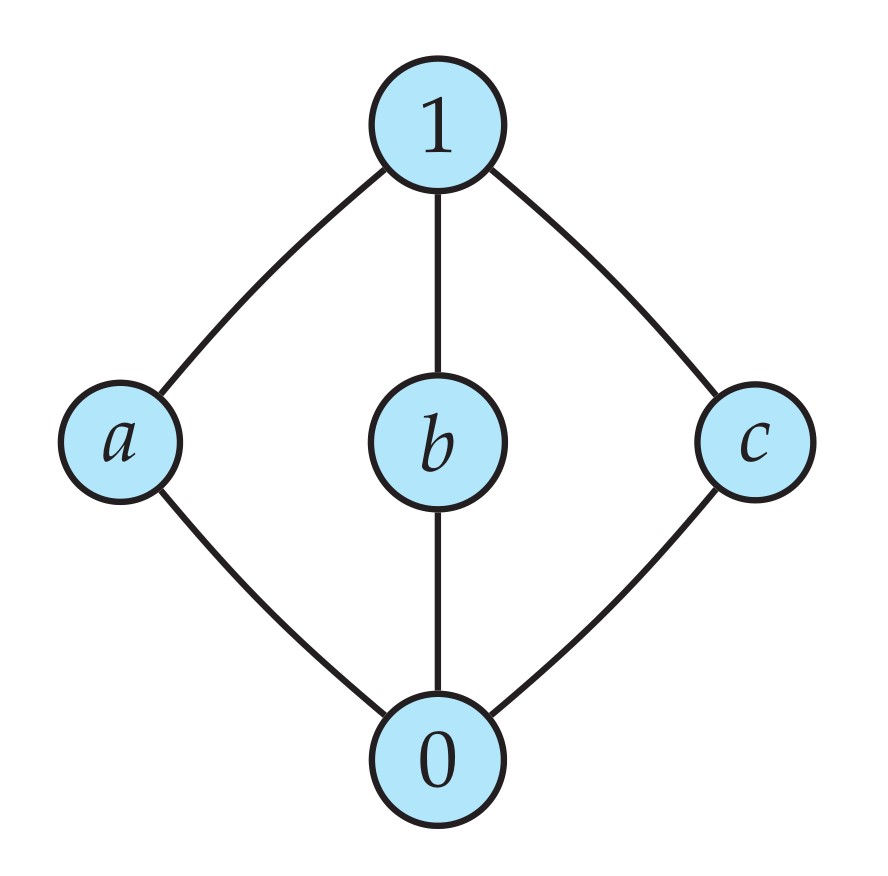
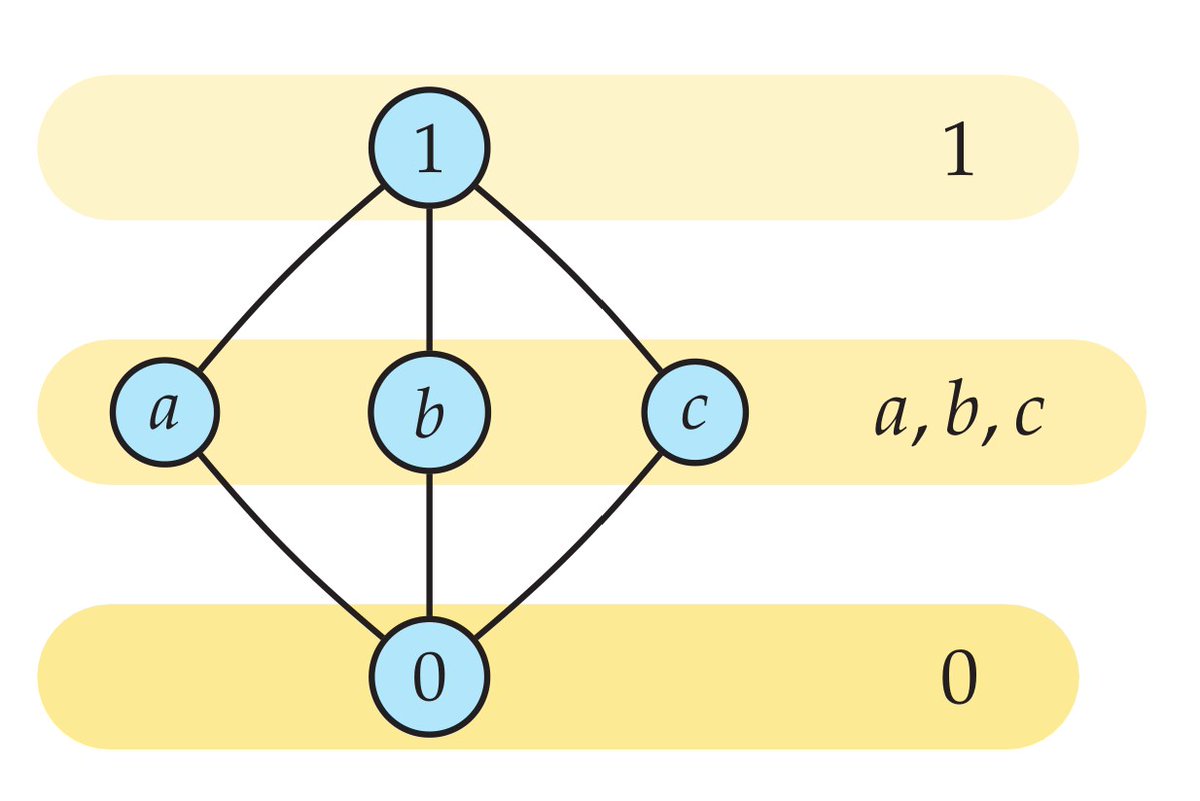
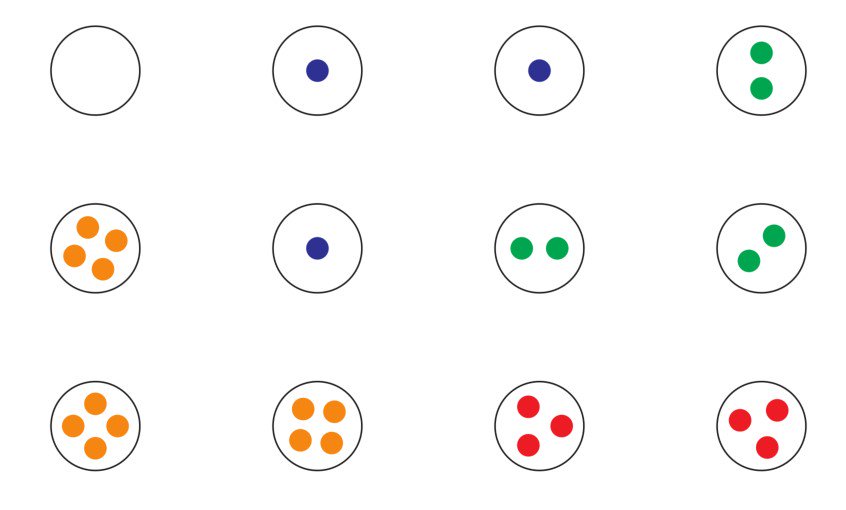
Foreshadowing — the algebra of orders. Here is an addition table for some simple finite orders. Did you know that you can add and multiply any two orders? A+B means a copy of A with a copy of B above. Stay tuned for multiplication... 
I expanded the addition table.
A larger expansion.
Bigger version.
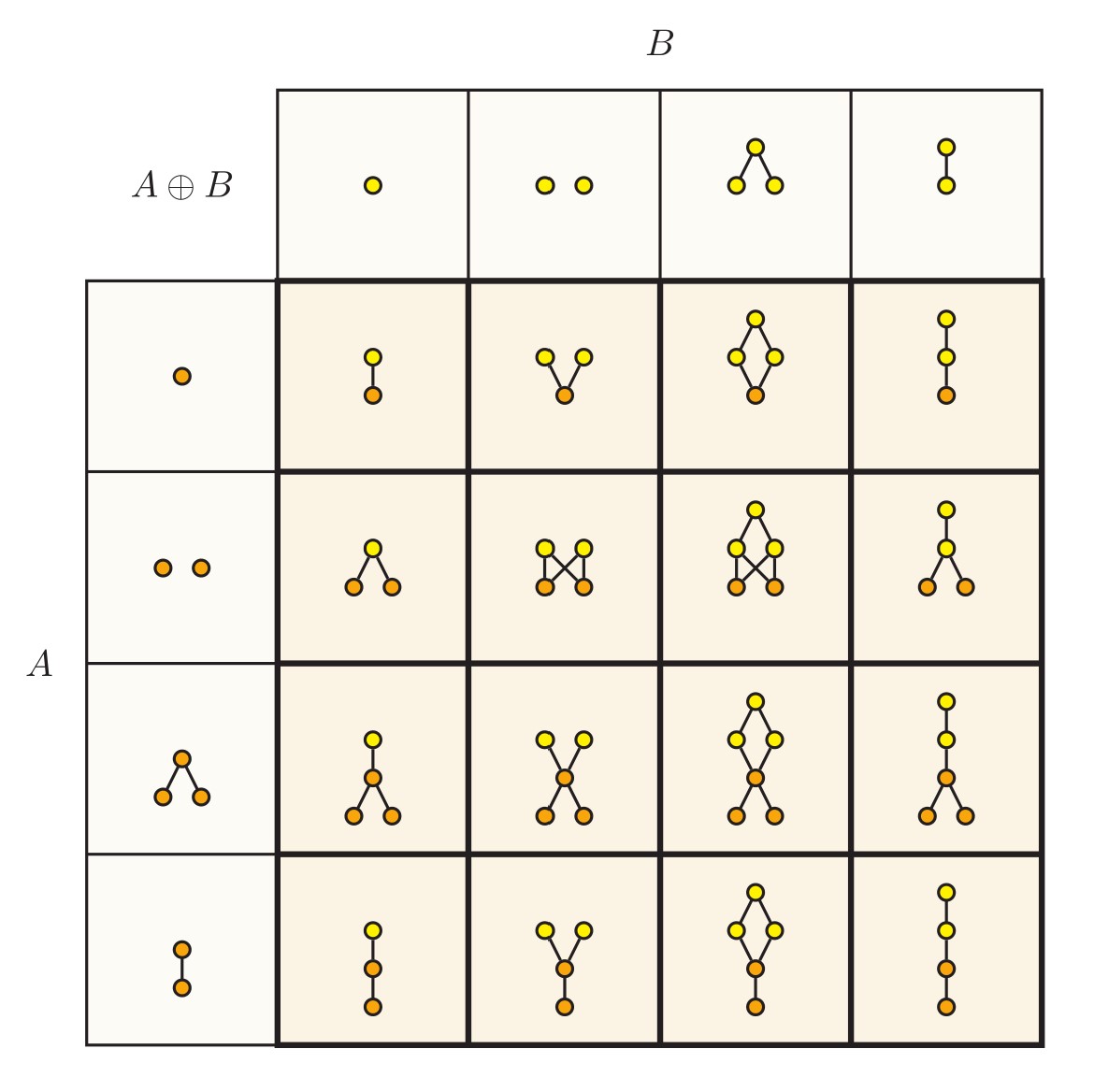
I am wondering whether the smaller tables might be pedagogically more effective in conveying the idea. The larger table might be offputting, whereas the small table is approachable. If you have a view on this, please let me know how to think about this for writing in my book.
• • •
Missing some Tweet in this thread? You can try to
force a refresh
