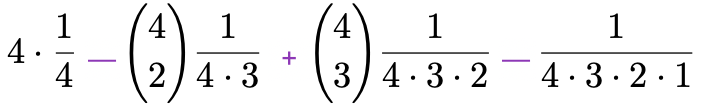¡Buenos días seres inciertos! Venga, vamos a ponernos la chaqueta que aquí ya refresca
Os cuento una posible solución del problema que so planteaba ayer. #StatsPill
Os cuento una posible solución del problema que so planteaba ayer. #StatsPill
https://twitter.com/AnaBayes/status/1453597679917875204?s=20
Lo que estamos buscando en este caso es la probabilidad de que alguna de ellas recupere su chaqueta.
En términos matemáticos, lo que estamos buscando es una unión de sucesos, donde cada uno de ellos es
Ai <- la chica i recupera su chaqueta.
En términos matemáticos, lo que estamos buscando es una unión de sucesos, donde cada uno de ellos es
Ai <- la chica i recupera su chaqueta.
Podríamos pensar que es el complementario de Ninguna recupera su chaqueta... y si somos capaces de calcular la probabilidad de que ninguna recupere su chaqueta, pues perfecto!
Pero a mi me gusta más pensarlo en términos de la ley de inclusión exclusión
Pero a mi me gusta más pensarlo en términos de la ley de inclusión exclusión
En su versión más básica nos dice que la probabilidad de la unión de dos sucesos es la suma de la probabilidad de cada uno de ellos menos la de la intersección.
Y si la generalizamos para cuatro sucesos como los que nos ocupan tenemos que la probabilidad de la unión es =
Y si la generalizamos para cuatro sucesos como los que nos ocupan tenemos que la probabilidad de la unión es =
Ahora, como son las probabilidades de las intersecciones. Podemos pensar que son un producto de probabilidades pero teniendo en cuenta que cuando una elija chaqueta, la otra ya habrá elegido.
Así, si pensamos que llegan en orden, la primera tendrá 1/4, la segunda 1/3...
Así, si pensamos que llegan en orden, la primera tendrá 1/4, la segunda 1/3...
Ojo, pensadlo, esto es así porque supongo que la anterior a cogido la suya, así que la chaqueta de la chica que llega a la percha sigue estando disponible.
Ahora solo nos queda hacer las multiplicaciones y pensar que en cada grupo de intersecciones hay más de una.
Por ejemplo, para las intersecciones de dos elementos tenemos chica 1 y chica 2, 1 y 3, 1 y 4, 2 y 3, 2 y 4 y, finalmente 3 y 4... en total 6 combinaciones
Por ejemplo, para las intersecciones de dos elementos tenemos chica 1 y chica 2, 1 y 3, 1 y 4, 2 y 3, 2 y 4 y, finalmente 3 y 4... en total 6 combinaciones
Con todo esto el resultado es que, la probabilidad de que al menos una coja su chaqueta es 0,625
Podemos extender el ejercicio a cualquier numero de coincidencias, incluso trabajar con la probabilidad de que en una baraja de cartas numeradas del 1 a X (siendo X el número de cartas), haya al menos una que en la que su número coincida con su posición después de barajarlas
Puede que se os haya ocurrido otra forma de calcularlo y me encantará leerla!!
Gracias por llegar hasta aquí y tened un día estupendo! 🥰
Gracias por llegar hasta aquí y tened un día estupendo! 🥰
• • •
Missing some Tweet in this thread? You can try to
force a refresh
