Thread by @MathisHammel

🧵THREAD : Le bitcoin, les blockchains, comment ça marche ?

On entend parler tous les jours de ces bases de données décentralisées qui sont censées révolutionner internet, mais connaissez-vous le fonctionnement étonnamment simple de cette technologie ?

Je vous explique ⤵️

Les blockchains ont été inventées fin 2008 via le Bitcoin, dans un papier signé par "Satoshi Nakamoto". On ne sait rien de cette personne, qui est peut-être un collectif.

Même s'il existe plein de types de blockchain, ce thread va se concentrer sur le fonctionnement de Bitcoin.

Petit disclaimer avant de commencer : bien que cryptographiquement superbe, je suis opposé à 99% de ce qui est fait avec les blockchains : entre sa consommation énergétique démesurée, les manipulations de marché et l'arnaque des NFT, difficile pour moi d'apprécier la technologie.

Bref, commençons : pourquoi "chaîne de blocs" ? On souhaite partager entre plein de gens un fichier contenant plein de virements qui arrivent en permanence.

Perso j'aurais fait un Google Docs, mais on va vite avoir des soucis de synchro et de modifications malveillantes 😋

Pour avoir un système fiable, tout le monde travaille sur un fichier en lecture seule sur lequel on ajoute de temps en temps un groupe de virements.

Faire un ajout à ce fichier demande beaucoup de puissance de calcul, et c'est donc un effort commun (on reviendra sur ce point).

C'est exactement comme ça que fonctionne une blockchain : chaque groupe de virements représente un bloc, et pour faire évoluer le "fichier" on ajoute un nouveau bloc à la suite des existants.

Chaque bloc contient le hash (un "résumé" cryptographique) du bloc précédent. Ainsi, un bloc repose sur tout l'édifice des blocs qui le précèdent, et il est impossible d'effacer discrètement une partie du passé de la blockchain.

Je vous explique dans un instant comment les virements peuvent être créées et authentifiés de manière sécurisée, mais d'abord on va voir pourquoi c'est si difficile d'ajouter un nouveau bloc à la blockchain et pourquoi il faut dépenser tant d'énergie pour le faire.

Pour éviter d'avoir des blocs trop petits et des évolutions dans tous les sens, on ajoute une contrainte aux blocs ajoutés : leur hash doit commencer par au moins 76 bits consécutifs à zéro (76 est la valeur actuelle mais elle évolue au cours du temps).

Pour avoir un tel bloc qui commence par plein de zéros, pas d'option facile : il faut tester des milliards et des milliards de configurations du bloc jusqu'à en trouver une dont le hash soit valide. Cette forme de bruteforce demande énormément de puissance de calcul.

Chacun va donc essayer de son côté de trouver un nouveau bloc valide qui contient les quelques transactions qui attendent d'être inscrites dans la blockchain.

Mais pourquoi les gens s'embêteraient-ils à dépenser du temps de calcul et de l'électricité pour ça ?

La réponse est simple : l'incentive.

Quand un utilisateur trouve un bloc, il a le droit d'ajouter une transaction spéciale : son compte se voit crédité de quelques bitcoins en récompense, qui sont "fabriqués" pour l'occasion et ne proviennent pas d'un autre compte.

Avoir plein d'ordinateurs (appelés mineurs) qui travaillent en parallèle sur le même problème permet de décentraliser le système de transactions, mais on fait également face à un problème de taille : que faire si deux blocs différents sont trouvés en même temps ?

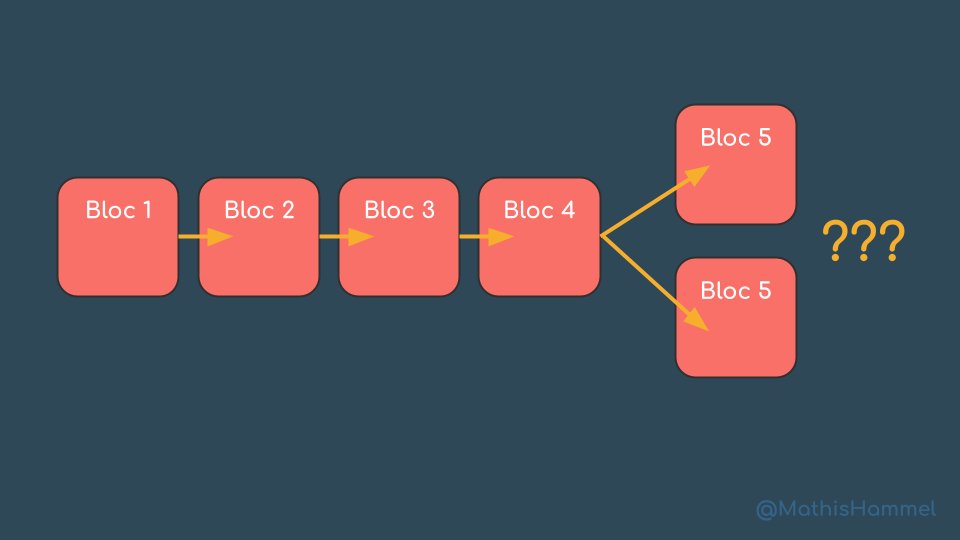
On pourrait avoir un système d'autorité centrale qui tranche et choisit un bloc parmi les deux, mais ça contredit le principe fondamental de décentralisation ! Du coup, on autorise la blockchain à avoir des divergences temporaires.

Les deux blockchains concurrentes (avec seulement le dernier bloc qui diffère) coexistent, jusqu'à ce qu'un nouveau bloc soit ajouté à l'une des deux branches.

Comme c'est toujours la chaîne la plus longue qui fait foi, l'alternative la plus courte sera ignorée.

C'est d'ailleurs pour ça que les virements peuvent prendre quelques heures : pour éviter d'accepter une transaction en tête de chaîne, on attend quelques blocs (appelés "confirmations") pour s'assurer que la transaction figure dans toutes les versions divergentes possibles.

Maintenant que vous comprenez mieux la structure d'une blockchain, je vous explique pourquoi seul le propriétaire d'un "compte" bitcoin est capable d'ordonner un virement depuis son wallet, même si n'importe qui peut insérer des transactions dans la blockchain.

Pour accéder à un portefeuille bitcoin, on n'utilise pas son email/mdp : chaque propriétaire est identifié par une adresse publique et détient la clé privée correspondante.

Pas besoin de s'inscrire pour détenir un portefeuille bitcoin, il suffit de générer une paire de clés.

Une transaction est un message qui transmet une certaine quantité de fonds d'une adresse A vers une adresse B, accompagnée d'une signature cryptographique de la clé privée A qui certifie que cet ordre de virement a bien été émis par le détenteur de la clé.

Dans chaque virement créé, l'émetteur inclut aussi un pourboire (les fees) qui reviendra au mineur du bloc correspondant. Comme chaque bloc contient un nombre de transactions limité, ce pourboire incite le mineur à inclure dans son bloc celles qui lui seront le plus rentables.

Un grand problème des blockchains par rapport à un système bancaire centralisé est que toutes les transactions sont forcément publiques. Mais comme les adresses ne sont pas directement rattachées à une identité, les échanges sont traçables mais restent entièrement anonymes.

Autre souci majeur : l'espace disque. Bitcoin a déjà enregistré près de 700 millions de transactions depuis 2009, soit plus de 350GB pour avoir sa propre copie de la chaîne. Mais il existe une optimisation remarquable qui réduit largement ce volume sans compromettre la sécurité.

En réalité, les transactions ne sont pas directement incluses dans les blocs : la blockchain est ultra légère, et chaque bloc pèse exactement 80 octets même si chacun contient plusieurs milliers de transactions.

Compression ultra efficace ? Non, arbres de Merkle !

Un arbre de Merkle est une structure optimisée pour calculer et vérifier un hash de plusieurs données (ici, les transactions d'un bloc). Pour calculer un arbre de Merkle, c'est simple : on prend le hash de chaque transaction, puis on concatène les hashs deux par deux :

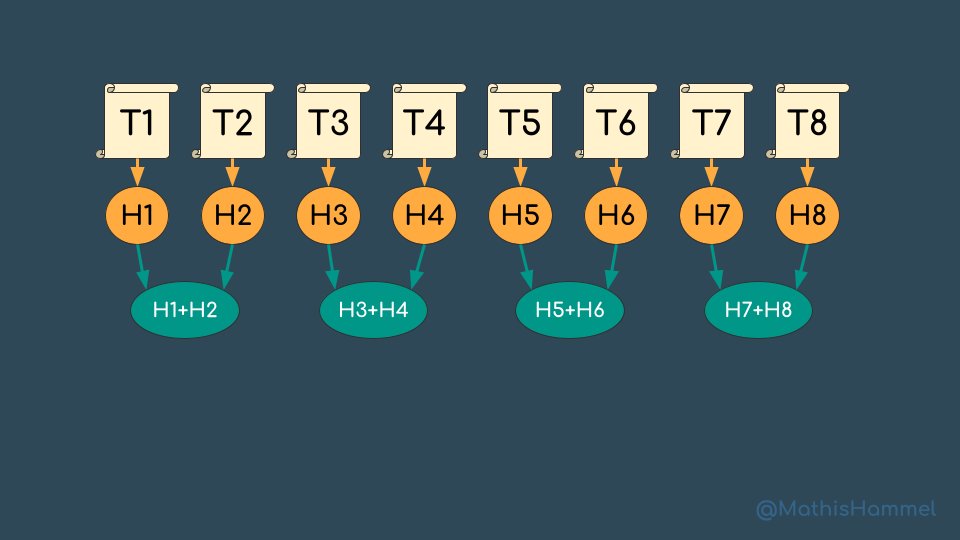
Ensuite on calcule le hash de chaque paire de hashs, et on recommence l'opération jusqu'à n'avoir qu'un seul hash. Tout cet ensemble forme une structure appelée arbre de Merkle, le noeud tout en bas est la racine de cet arbre et c'est cette racine que l'on inclut dans le bloc.

Du coup les transactions ne sont pas dans la blockchain, on utilise leur représentation ultra-condensée à la place. Comme la fonction de hachage (SHA256) est sécurisée, on considère qu'il est impossible de fabriquer un ensemble de transactions différent ayant la même racine.

Mais pourquoi utiliser l'arbre de Merkle alors que le hash de toutes les transactions concaténées fonctionnerait tout aussi bien ?

C'est une question de performance lors de la validation des transactions.

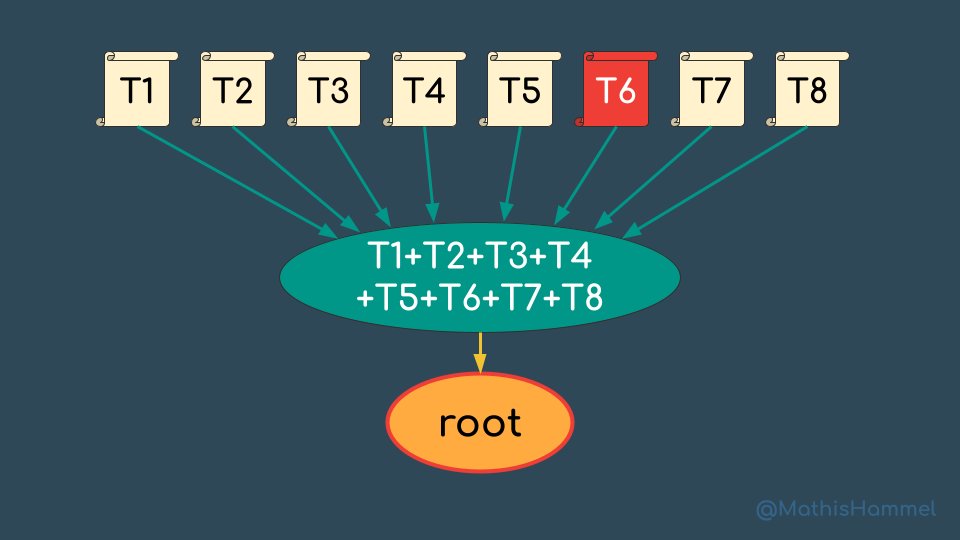
Admettons que j'envoie un peu de bitcoin vers le wallet d'un restaurant pour payer mon repas. La preuve de paiement consiste à démontrer que ma transaction (ici T6) figure bien dans l'un des blocs de la blockchain.

Si la blockchain utilisait le hash de toutes les transactions du bloc qui était utilisé au lieu de la racine de Merkle, je devrais fournir une copie des 8 transactions pour que le destinataire recalcule le hash et vérifie qu'il correspond bien au bloc donné.

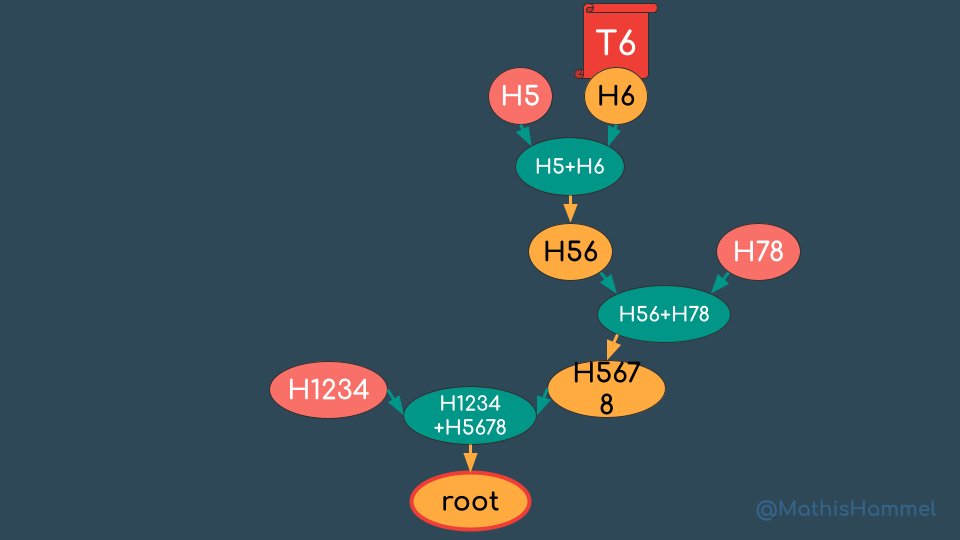
Au contraire, avec l'arbre de Merkle, je dois seulement fournir une copie de ma transaction T6 ainsi que les hashs H5, H7-8 et H1-4.

Avec seulement ces 4 données, je peux prouver de manière irréfutable que l'arbre de Merkle contient ma transaction.

Toujours pas convaincu.e ? C'est normal.

L'arbre de Merkle marche sur de grands ensembles de données. Pour un bloc d'un million de transactions, une preuve de transaction demande seulement 19 hashs pour remonter jusqu'à la racine, soit un volume 52 000 fois plus petit !

À retenir de ce thread :

- 1 bloc = hash du bloc précédent + racine Merkle
- Création de blocs = bruteforce très lent
- Récompense minage via l'incentive et les fees
- Transaction = signature avec clé privée de l'émetteur

Vous en voulez encore ? Ok, voici un chapitre bonus ;)

L'école @Guardia_School m'a demandé de vous parler un peu de cybersécurité, et ça tombe bien parce qu'il existe plein d'attaques contre les blockchains !

Je vais vous en présenter une qui était déjà identifiée par Satoshi en 2008, et une autre qui utilise du calcul quantique 😍

La toute première attaque sur les blockchains fut baptisée "attaque des 51%". Ce nom vient du fait qu'il faut détenir plus de la moitié de la puissance de minage, autant vous dire que pour bitcoin il faut prévoir un sacré budget ! (mais ça a déjà été vu sur d'autres blockchains)

Le principe est simple : après avoir payé une Ferrari en bitcoins, on reprend une vieille copie de la blockchain (antérieure à notre transaction) et on utilise notre puissance de calcul énorme pour générer une chaîne alternative où nos bitcoins n'ont pas bougé.

Comme on dispose de plus de 50% de la puissance, on va plus vite que tous les autres mineurs réunis et on peut créer une chaîne plus longue.

Et comme c'est la plus longue chaîne qui est reconnue, on peut réécrire l'histoire à volonté pour faire disparaître des transactions !

Une autre famille d'attaques cool implique l'utilisation d'un ordinateur quantique. Actuellement personne ne dispose d'un tel calculateur, mais si cette technologie voyait le jour (certains spéculent un horizon 2030) elle mettrait fin au bitcoin et plein d'autres blockchains.

Les transactions bitcoin sont signées via le cryptosystème ECDSA, qui est actuellement le standard principal dès qu'il s'agit de faire des signatures cryptographiques (c'est notamment ce qui sécurise les pass sanitaires en France). Mais ECDSA est menacé d'extinction.

En utilisant l'algorithme de Shor sur un ordinateur quantique, il est possible de casser n'importe quelle clé privée ECDSA pour voler l'argent du wallet correspondant. Le calcul quantique sera une révolution énorme pour internet, et la disparition de bitcoin en fera partie.

Et même pour les autres blockchains utilisant des signatures résistantes à l'algorithme de Shor, il existe toujours l'algorithme de Grover qui rendra inutile toute forme de minage.

La seule alternative viable sera le Proof of Stake, et la planète nous en remerciera !

Pour revenir un peu sur @Guardia_School dont je vous parlais plus tôt : c'est une école de cybersécurité (bac+3 et bac+5) que je parraine, la première rentrée aura lieu en 2022 et les candidatures sont déjà ouvertes. Plus d'infos sur guardia.school !

J'espère que ce long thread vous a plu, et félicitations d'être arrivé au bout !

Il m'a pris énormément de temps à préparer mais j'en suis super fier, je serai archi reconnaissant si vous le partagez via un retweet, ou un message pour vos proches/collègues à l'esprit curieux ;)

Quelques ressources supplémentaires :

- Le papier original de Satoshi Nakamoto : bitcoin.org/bitcoin.pdf

- Un autre thread pour comprendre les signatures cryptographiques, où j'ai utilisé comme exemple le QR code infalsifiable du pass sanitaire :

https://twitter.com/MathisHammel/status/1419268005909962756