
1/
Get a cup of coffee.
In this thread, I'll walk you through Recurrence Equations.
This is a beautiful area of math, with many finance/investing applications.
Plus, it can teach us a lot about problem solving in general -- how to simplify problems and solve them efficiently.
Get a cup of coffee.
In this thread, I'll walk you through Recurrence Equations.
This is a beautiful area of math, with many finance/investing applications.
Plus, it can teach us a lot about problem solving in general -- how to simplify problems and solve them efficiently.

2/
The idea for this thread came from a puzzle I posed on Twitter a couple days ago.
It was a fairly simple counting exercise:
If we toss a coin 10 times, there are 2^10 = 1024 possible outcomes. How many of these WON'T contain 2 consecutive Tails?
The idea for this thread came from a puzzle I posed on Twitter a couple days ago.
It was a fairly simple counting exercise:
If we toss a coin 10 times, there are 2^10 = 1024 possible outcomes. How many of these WON'T contain 2 consecutive Tails?

3/
About 800 people responded to the poll.
But unfortunately, only ~23% of them picked the right answer.
The other ~77% got it wrong.
About 800 people responded to the poll.
But unfortunately, only ~23% of them picked the right answer.
The other ~77% got it wrong.

4/
So, most likely, many of us don't have good mental models for thinking about these kinds of questions.
If these questions are nails, many of us aren't equipped with the right kind of hammer to take to them.
So, most likely, many of us don't have good mental models for thinking about these kinds of questions.
If these questions are nails, many of us aren't equipped with the right kind of hammer to take to them.
5/
Enter Recurrence Equations -- a super-powerful math technique.
Once we know this technique, we'll be able to solve not just this question, but a whole host of others with all kinds of important applications to finance, investing, etc.
So, let's dive in!
Enter Recurrence Equations -- a super-powerful math technique.
Once we know this technique, we'll be able to solve not just this question, but a whole host of others with all kinds of important applications to finance, investing, etc.
So, let's dive in!
6/
Imagine we toss a coin repeatedly. Say, N times.
Each time, we get a Heads (H) or a Tails (T).
But if we get 2 *consecutive* Tails -- ie, the pattern TT -- it's Game Over.
Our goal is to figure out how many ways we can *survive* N tosses *without* seeing this dreaded TT.
Imagine we toss a coin repeatedly. Say, N times.
Each time, we get a Heads (H) or a Tails (T).
But if we get 2 *consecutive* Tails -- ie, the pattern TT -- it's Game Over.
Our goal is to figure out how many ways we can *survive* N tosses *without* seeing this dreaded TT.
7/
Here's a "State Transition Diagram" to help us visualize this "avoid TT" game.
We start at state S1. We toss our coin to get a H or T.
If it's a H, we follow the H arrow, which keeps us in S1.
But if it's a T, we follow the T arrow, which takes us to S2.
And so on.
Here's a "State Transition Diagram" to help us visualize this "avoid TT" game.
We start at state S1. We toss our coin to get a H or T.
If it's a H, we follow the H arrow, which keeps us in S1.
But if it's a T, we follow the T arrow, which takes us to S2.
And so on.

8/
Thus, at any given time, we are in one of 3 states: S1, S2, or S3.
We toss our coin, get our H or T, and based on this decide which arrow to follow *out of* our current state and *in to* our next state.
And at the next state, we rinse and repeat.
Thus, at any given time, we are in one of 3 states: S1, S2, or S3.
We toss our coin, get our H or T, and based on this decide which arrow to follow *out of* our current state and *in to* our next state.
And at the next state, we rinse and repeat.
9/
We've constructed our diagram in such a way that, if we *ever* see a TT, we'll be in state S3 (the "Game Over" state) by the end of the TT.
And once we've seen TT and reached S3, there's no escape. We stay in S3 forever -- no matter whether future coin tosses are Hs or Ts.
We've constructed our diagram in such a way that, if we *ever* see a TT, we'll be in state S3 (the "Game Over" state) by the end of the TT.
And once we've seen TT and reached S3, there's no escape. We stay in S3 forever -- no matter whether future coin tosses are Hs or Ts.
10/
The idea is: we *never* want to get to S3.
That is, we want to count the number of ways we can toss our coin N times, and at the end of these N tosses, end up in either S1 or S2. Not S3.
All "TT less" outcomes will leave us in either S1 or S2.
The idea is: we *never* want to get to S3.
That is, we want to count the number of ways we can toss our coin N times, and at the end of these N tosses, end up in either S1 or S2. Not S3.
All "TT less" outcomes will leave us in either S1 or S2.
11/
This suggests a logic for *counting* such "TT less" outcomes.
We "work backwards".
If we know where we want to be after N tosses, then we ask ourselves: where all can we be after "N minus 1" tosses? After "N minus 2" tosses? And so on.
Here's the reasoning:


This suggests a logic for *counting* such "TT less" outcomes.
We "work backwards".
If we know where we want to be after N tosses, then we ask ourselves: where all can we be after "N minus 1" tosses? After "N minus 2" tosses? And so on.
Here's the reasoning:

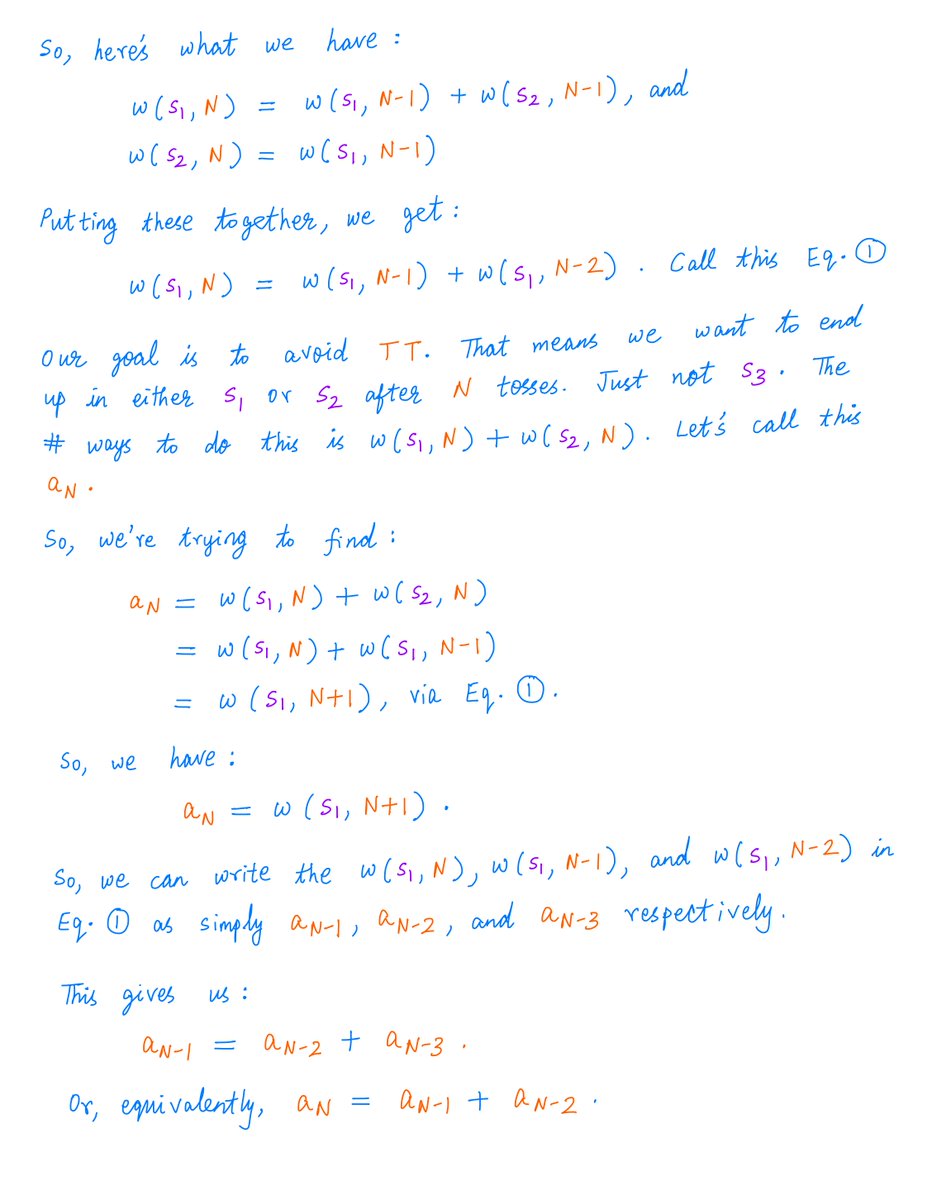

12/
The end result of following the logic above is a Recurrence Equation.
This equation gives us a "recipe" for finding a_N -- the number of "TT less" outcomes after N tosses.
The recipe is: First find a_{N minus 1}. Then find a_{N minus 2}. Then add them up. That's a_{N}.
The end result of following the logic above is a Recurrence Equation.
This equation gives us a "recipe" for finding a_N -- the number of "TT less" outcomes after N tosses.
The recipe is: First find a_{N minus 1}. Then find a_{N minus 2}. Then add them up. That's a_{N}.

13/
For example, we want to find a_10 -- the number of "TT less" outcomes after 10 tosses.
By repeatedly using our Recurrence Equation recipe, we find that a_10 is 144.
Like so:
For example, we want to find a_10 -- the number of "TT less" outcomes after 10 tosses.
By repeatedly using our Recurrence Equation recipe, we find that a_10 is 144.
Like so:
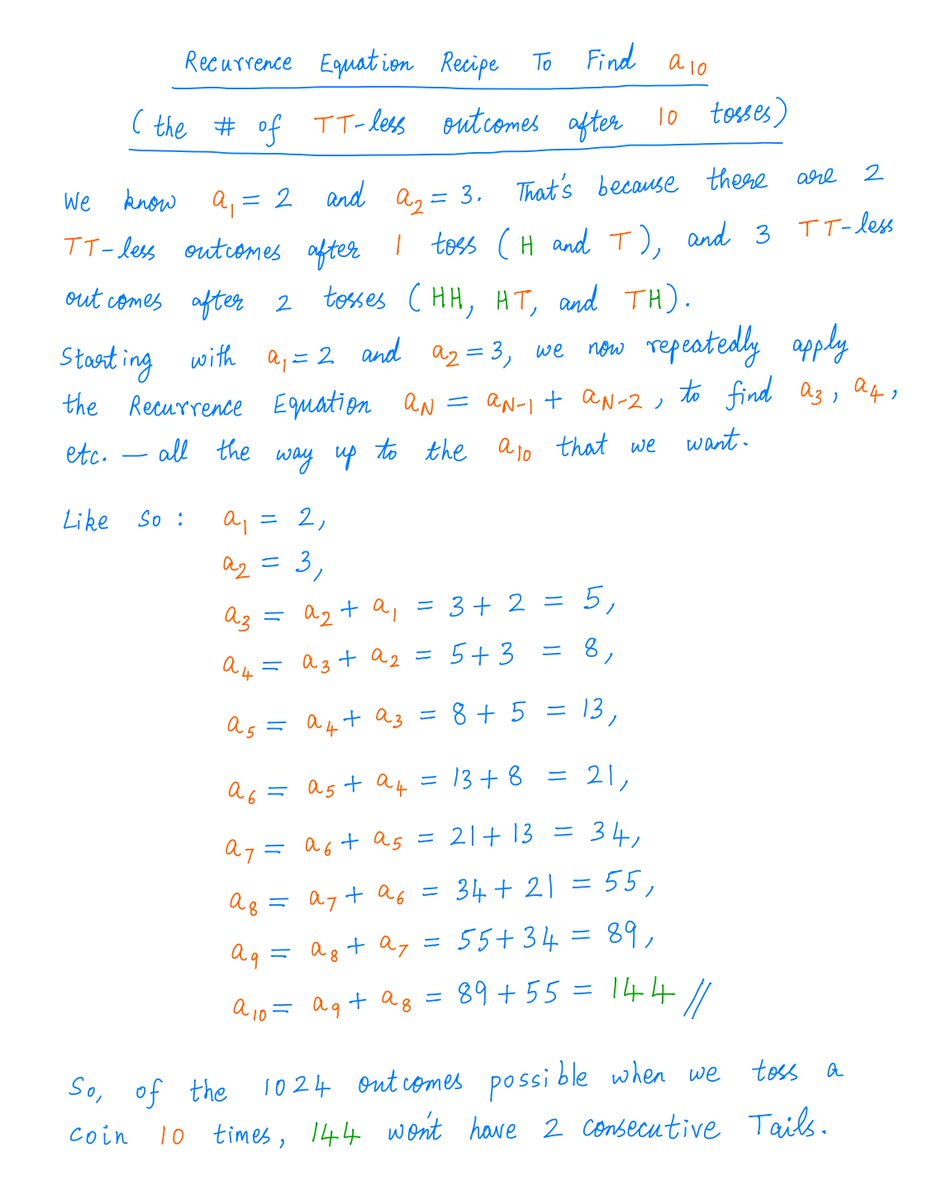
14/
Recurrence Equations are beautiful. They solve problems by *simplifying* them.
We break down a big problem into small, simple sub-problems.
We use the solutions to these sub-problems to *incrementally* build a solution to the big problem.
Brick by brick, we build a house.
Recurrence Equations are beautiful. They solve problems by *simplifying* them.
We break down a big problem into small, simple sub-problems.
We use the solutions to these sub-problems to *incrementally* build a solution to the big problem.
Brick by brick, we build a house.
15/
Recurrence Equations can be *automated* pretty easily as well.
Once we know that a_N = a_{N minus 1} + a_{N minus 2}, it's easy to create an Excel spreadsheet or a Python program to calculate a_10.
Or a_100.
Or a_1000.
Recurrence Equations can be *automated* pretty easily as well.
Once we know that a_N = a_{N minus 1} + a_{N minus 2}, it's easy to create an Excel spreadsheet or a Python program to calculate a_10.
Or a_100.
Or a_1000.
16/
And if we learn a bit of math, we can also solve many Recurrence Equations *exactly*.
This can give us direct formulas for whatever we want to find. So, we won't even need a spreadsheet or computer program.
For example, here's an exact solution to our "TT less" problem:

And if we learn a bit of math, we can also solve many Recurrence Equations *exactly*.
This can give us direct formulas for whatever we want to find. So, we won't even need a spreadsheet or computer program.
For example, here's an exact solution to our "TT less" problem:

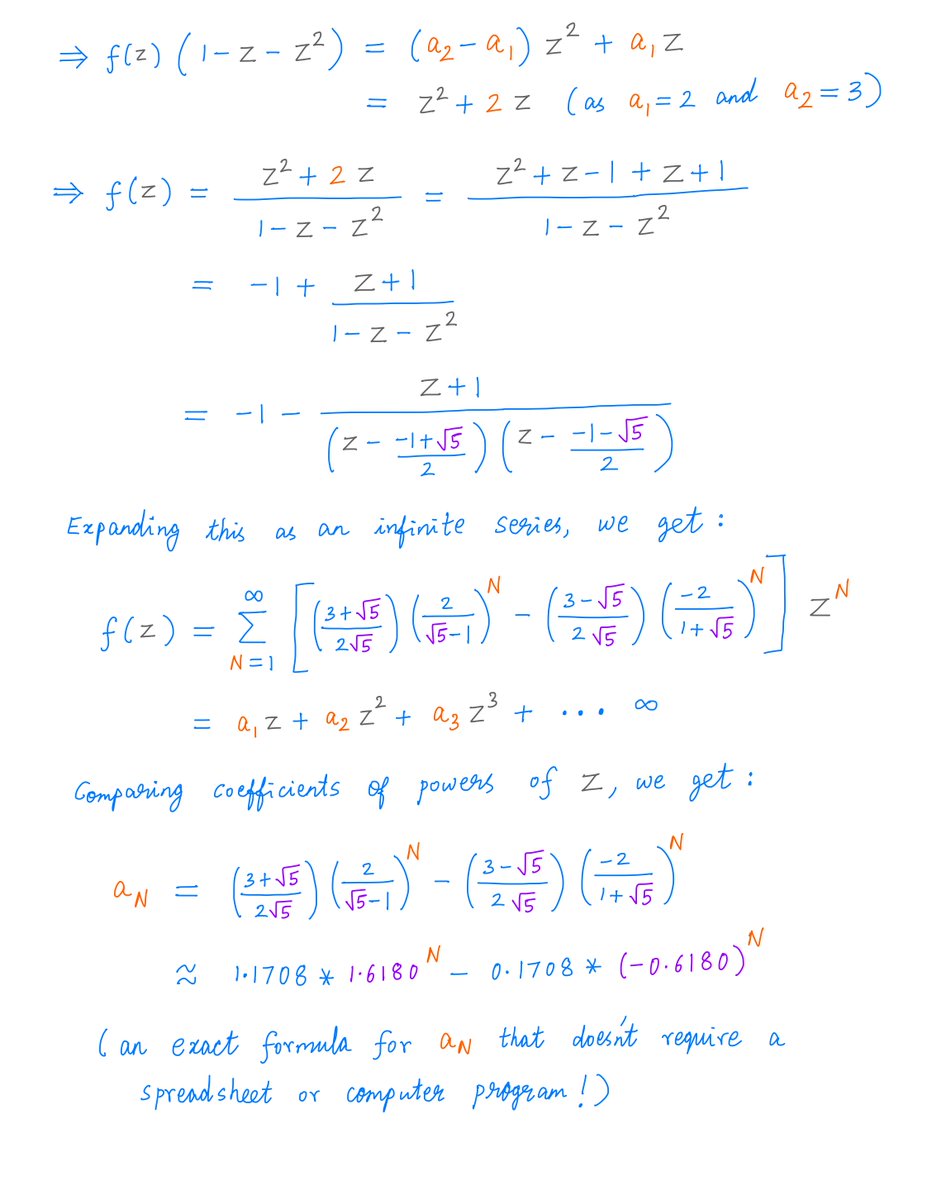
17/
To find the exact solution above, I used the method of "Generating Functions".
Knowing this method can help us solve various Recurrence Equations that frequently arise in finance and investing.
For more:
To find the exact solution above, I used the method of "Generating Functions".
Knowing this method can help us solve various Recurrence Equations that frequently arise in finance and investing.
For more:
https://twitter.com/10kdiver/status/1426597150993965057
18/
And the math can give us special insights.
For example, our "TT less" Recurrence Equation (a_N = a_{N minus 1} + a_{N minus 2}) happens to be the famous Fibonacci Recurrence.
Mathematicians have studied it for centuries and discovered all kinds of cool things about it!
And the math can give us special insights.
For example, our "TT less" Recurrence Equation (a_N = a_{N minus 1} + a_{N minus 2}) happens to be the famous Fibonacci Recurrence.
Mathematicians have studied it for centuries and discovered all kinds of cool things about it!
19/
For instance, one well-known property of the Fibonacci Recurrence is that, as we take N to infinity, the ratio of successive a_Ns will quickly converge to the Golden Ratio, (1 + sqrt(5))/2.
That's approximately 1.618.
en.wikipedia.org/wiki/Golden_ra…
For instance, one well-known property of the Fibonacci Recurrence is that, as we take N to infinity, the ratio of successive a_Ns will quickly converge to the Golden Ratio, (1 + sqrt(5))/2.
That's approximately 1.618.
en.wikipedia.org/wiki/Golden_ra…
20/
So, as we toss our coin more and more times, the number of "TT less" outcomes grows at roughly 62% with each additional toss.
But the *total* number of possible outcomes *doubles* with each additional toss.
So, the *probability* of a "TT less" outcome will go to zero.
So, as we toss our coin more and more times, the number of "TT less" outcomes grows at roughly 62% with each additional toss.
But the *total* number of possible outcomes *doubles* with each additional toss.
So, the *probability* of a "TT less" outcome will go to zero.
21/
Also, here's a surprising fact.
What if we want "HT less" outcomes instead of "TT less" outcomes?
It turns out that "HT less" outcomes are far rarer than "TT less" outcomes -- even though HT and TT have the exact same likelihood if our coin is fair!

Also, here's a surprising fact.
What if we want "HT less" outcomes instead of "TT less" outcomes?
It turns out that "HT less" outcomes are far rarer than "TT less" outcomes -- even though HT and TT have the exact same likelihood if our coin is fair!


22/
All kinds of financial models use Recurrence Equations.
For example, when companies grow by retaining and re-investing part of their earnings, this growth is usually modeled as a Recurrence Equation:
All kinds of financial models use Recurrence Equations.
For example, when companies grow by retaining and re-investing part of their earnings, this growth is usually modeled as a Recurrence Equation:
https://twitter.com/10kdiver/status/1292130867234484227
23/
Similarly, if we take out a mortgage to buy a house, our monthly payments are calculated using a Recurrence Equation:
Similarly, if we take out a mortgage to buy a house, our monthly payments are calculated using a Recurrence Equation:
https://twitter.com/10kdiver/status/1279100941115944961
24/
So, once we learn some general techniques to formulate and solve Recurrence Equations (like the techniques in this thread), many different kinds of financial calculations immediately become a breeze.
So, once we learn some general techniques to formulate and solve Recurrence Equations (like the techniques in this thread), many different kinds of financial calculations immediately become a breeze.
25/
Please join me tomorrow (Sun, Feb 26) at 1pm ET for a new episode of Money Concepts.
We'll talk about Recurrence Equations, how to model financial situations using them, how to solve them and glean insights from them, etc.
Link: callin.com/link/EcmhyBCbIb
Please join me tomorrow (Sun, Feb 26) at 1pm ET for a new episode of Money Concepts.
We'll talk about Recurrence Equations, how to model financial situations using them, how to solve them and glean insights from them, etc.
Link: callin.com/link/EcmhyBCbIb
26/
About Money Concepts
We're a virtual investing club. Our goal is to help each other become better investors.
We meet Sundays at 1pm ET via @getcallin, to discuss all things investing.
Join us. Get the app. Subscribe. Tell your friends.
It's FREE.
callin.com/show/money-con…
About Money Concepts
We're a virtual investing club. Our goal is to help each other become better investors.
We meet Sundays at 1pm ET via @getcallin, to discuss all things investing.
Join us. Get the app. Subscribe. Tell your friends.
It's FREE.
callin.com/show/money-con…
27/
Recurrence Equations may seem rather mathematical and esoteric.
But learning about them greatly improved my financial numeracy, and helped me understand all kinds of financial calculations better.
I hope this thread helped you as well.
Have a great weekend!
/End
Recurrence Equations may seem rather mathematical and esoteric.
But learning about them greatly improved my financial numeracy, and helped me understand all kinds of financial calculations better.
I hope this thread helped you as well.
Have a great weekend!
/End
• • •
Missing some Tweet in this thread? You can try to
force a refresh










