Thread by @PikumaLondon

You know I always add some #math spice into my #gamedev courses, and that usually means touching some cool linear algebra.

But something most students still struggle with is the *intuition* behind the #Determinant of a matrix.

Let's quickly look at it together...🙂

[1/18] 🧵

Since we are really interested in building some *intuition*, let's look at the determinant of a 2x2 matrix first.

When we were in high school, we learned that the determinant of a 2x2 matrix is given by:

| a b |
| c d | = a*d - b-c

But, where does that come from?

[2/18]

Seki Kōwa was a Japanese mathematician from the Edo period, and he was sometimes described as "Japan's Newton."

He had Samurai origins but was adopted into the noble Seki family, subject of the shōgun.

As a kid, it was visible that he had great potential with numbers.

[3/18]

Seki Kōwa was involved in feudal accounting and also surveying reliable maps for his employer's land.

In 1684, his job required him to start looking at Linear systems.

A linear system is a set of *linear* equations that need to be true together (as a system).

[4/18]

Oh, and just to make sure we are all on the same page, linear equations are equations that represent functions with solutions that form a line in the Euclidean plane (...duh).

We put these equations in a system when they all need to hold true at the same time.

[5/18]

In the example above... a, b, c, d, e, and f are known numbers (usually ∈ ℝ).

What we are really interested in is finding the values of (x) and (y) that satisfy that system, making the equality true, together.

[6/18]

This was how Seki Kōwa approached this problem:

We'll try finding the value of x first.

From algebra, we know that we can multiply both sides of the equation by something and the equality is still true.

Therefore, we're going to multiply the entire first equation by d.

[7/18]

And now, we are going to also multiply the entire second equation by b.

And look... I know this is weird but keep in mind that the main reason we are doing this is because we are trying to cancel "y" terms out from the final solution so we can find "x".

[8/18]

And here's the magic. We will *subtract* both equations, which will hopefully cancel the "y" terms out.

We get as a result: adx-cbx = de-bf

[9/18]

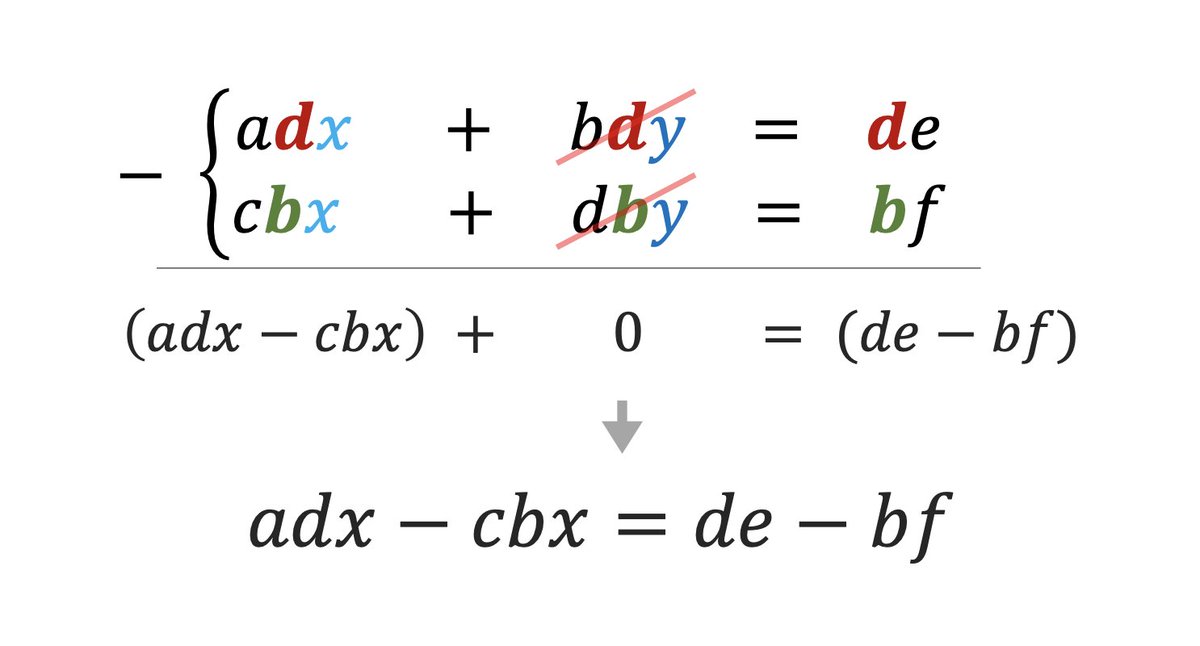
Now that we canceled the y term out and we have only x left, let's go ahead and find our x.

Using simple algebra, if we factor x out on the left side, and then divide everything by (ad-cb), we get our x.

[10/18]

Cool... do you see how x is written as a fraction?

Here comes the most important part of this post.

Do you agree that we might have an issue if the denominator (bottom part) of this fraction is *zero*?

Therefore, (ad*cb) "DETERMINES" something about our system!!!

[11/18]

Let me repeat that again!!!

That denominator of this fraction is the "DETERMINANT" that *determines* if we might have a problem when solving our system.

Therefore, it is a #Determinant of that system.

[12/18]

Let's write this down:

1. If the denominator is different than zero, we have no problem (and the system has a unique solution).

2. If the denominator is zero, we'll have a problem finding a solution for that system.

It all depends on the *determinant* of that system.

[13/18]

Independently, in 1693 (~10 years after Seki Kōwa's discovery), Gottfried Leibniz proposed something similar in a letter that he wrote to the French mathematician l'Hopital.

[14/18]

Seki Kōwa and Leibniz discovered it, but it was Carl Gauss who first used the name "determinant" in 1801.

Oh, the intuition behind the determinant of 2x2 systems is the same for other dimensions. Of course... the bigger the matrix, the trickier the determinant gets.

[15/18]

And just to conclude, you'll see also a geometrical interpretation for the determinant.

We can realize that the determinant of a 2x2 matrix is the area of the parallelogram defined by the vectors of our matrix.

Once again, if that area is zero... no bueno!

[16/18]

Actually, let me rephrase that... not just the area of a parallelogram (as in our 2x2 case), but also the *volume* of the parallelepiped defined by the vectors of our matrix in higher dimensions.

[17/18]

And that's as far as we'll go on a Twitter thread.

I hope you enjoyed the quick review. Some call this "trivial", but you'd be surprised to see how many people don't grok this.

If you like it, share it with others! 😉

You'll find more at pikuma.com.

See you soon!

Ugh! I know, I know... I made some typos. 🥲

Well... apparently I was the one that skip that lecture. 😅

The determinant is a*d-b*c.