Thread by @benwilbrink

'Meten is weten', werkelijk?
Docenten stellen bij proefwerken, toetsen, tentamens, examens, vast of antwoorden op de gestelde vragen juist zijn, of niet.
Wij staan er omheen en kijken ernaar. Weten we nu iets? Jazeker. Kunnen we dat wat we nu weten ook duiden? Ai.

Ik wil het over summatieve toetsen hebben: er staat iets op het spel. Wat op het spel staat zijn de mogelijke (gevolgen van) beslissingen op basis van resultaten op de toets. Een specifieke onderverzameling daarvan is wat we (internationaal) 'validiteit' noemen:

de mate waarin de toets leidt tot juiste beslissingen. Hé, dat is best opmerkelijk: het gaat niet om de meting zelf, maar om de beslissing op basis van de meting. Meten is beslissen, zou je denken. Dit klinkt ingewikkelder dan meten is weten, en dat is het ook. De reden om

toch voor het complexe te gaan is, ik geef een voorlopige kenschets, dat de meting/toets in het onderwijs nooit het doel zelf is. Het zou prettig zijn altijd een helder antwoord te hebben of te krijgen op de vraag naar het doel van de beoordeling (toets, examen, etc).

Toch ben ik weinig onderzoek tegengekomen waar betreffende docenten de gelegenheid kregen zich over het doel van hun toets uit te spreken. Ik ben zelf in de gelegenheid geweest zo'n onderzoekje te doen: benwilbrink.nl/publicaties/04… Nou, de opvattingen lopen sterk uiteen hoor.

Dat doet denken aan een vragenlijst voor bezoekers van een congres over zittenblijven (Alfred Wald (1985). 'Een jaartje overdoen. Verslag van het SVO-symposium over zittenblijven in het voortgezet onderwijs', SVO, p. 135-150):

Dat laat prachtig zien dat iedereen maar wat doet en denkt, dat het zittenblijven dus vooral folklore is. 'Iedereen': zo'n 150 schoolleiders als ik mij niet vergis. Ieder school heeft weer andere regels voor de overgang. [Niet online beschikbaar — Google weet niet alles]

Waar het mij om te doen is: voor de leerling of student zijn er altijd ernstige gevolgen verbonden aan summatieve toetsen. En omdat zij verondersteld worden zich goed voor te bereiden op die toetsen, werken die toetsen bovendien op de aard van die voorbereiding: #feedforward.

Toetsen zijn maar rare meetinstrumenten: ze hebben serieuze consequenties (zoals civiel effect van examens), en omdat die consequenties er zijn, hebben ze ook serieuze invloed op hoe leerlingen zich voorbereiden op de toets, EN ZO DE METING ZELF BEÏNVLOEDEN.

Dit fenomeen zien we overigens breder dan in het onderwijs alleen. Wim Hofstee schreef er ooit een aardig boek over: 'Psychologische uitspraken over personen. Beoordeling/voorspelling/advies/test'. Betrokken personen praten altijd terug. Rotsen doen dat niet bij hun beoordeling.

Hoe nu verder? ik word overrompeld door de vele mogelijkheden. Maar dat ga ik kortsluiten. Ik kom zeker nog te spreken over cijfers, cijfergeven, zak-slaaggrenzen, modelleren van toetsscores, en nog zo wat. Maar eerst wil ik dit TOETSEN met zijn gevolgen en zijn #feedforward

of ook #washback of #backwash contrasteren met wat typisch het geval is voor 'echte' psychologische tests, zoals intelligentie- en persoonlijkheidstests. Bij deze TESTS neemt de psycholoog aan dat er geen doeltreffende voorbereiding op is geweest, anders dan uitgerust zijn.

Voor het ontwikkelen en gebruiken van psychologische tests is sinds ongeveer 1900 een een steeds complexer uitgebouwd wiskundig instrumentarium ontwikkeld dat psychometrie heet. Men wilde de geest meten, nietwaar. Bij dit TESTEN vinden we een sterke oriëntatie op meten. Yes.

Maar heel dat wiskundig apparaat berust op de aanname dat iedereen die getest wordt, in gelijke mate NIET inhoudelijk op dat testen is voorbereid. In de mate waarin die aanname geschonden is, struikelt de psychometrie over de eigen formalismen. Ik geef een historisch voorbeeld:

De eerste tests (Army Beta, maar dat moet ik nog checken) die in 1917 in de VS werden ingezet voor het selecteren van rekruten voor het Amerikaanse leger bestonden uit meerkeuzevragen. De instructie was: weet je het antwoord niet, laat de vraag dan open. Wat gebeurt? Men kwam

er al gauw achter dat je kans om in het leger te komen groter was wanneer je die instructie in de wind sloeg, dus toch een antwoord 'gokte' bij niet weten. Dan leidt de test niet tot valide beslissingen. De psychologen namen hun verlies, en veranderden de testinstructie.

Het beroerde van deze ontwikkeling is dat ook schooltoetsen werden ontwikkeld naar het voorbeeld van de zo succesvolle intelligentietests, met meerkeuze en met de gekkigheid van raden en al. A.D. de groot was bij een bezoek aan de VS diep onder de indruk van deze 'studietoetsen'

en voerde bij ommekomst in Nederland een felle campagne om ze hier ook geïntroduceerd te krijgen, als 'objectieve' studietoetsen. Dat laatste was ideologische overdrijving (zie mijn 1977 benwilbrink.nl/publicaties/77…) maar het kwaad was al geschied. Nog steeds lijdt het Nederlandse

onderwijs onder de misvatting dat meerkeuzetoetsen 'objectief' zijn, en dat het in het onderwijs oké zou zijn leerlingen die iets niet weten, maar een antwoord te laten gokken. Dit is een vorm van loten waar ik mordicus tegen ben, haha. Twintig jaar lang kruisjes zetten ook.

Mijn voorbeeld is een beetje uit de hand gelopen. Pun intended. Maar het is ook een voorbeeld hoe schadelijk het is wanneer het onderwijs technieken uit een ander domein (de psychometrie) overneemt zonder enige kritische reflectie of dit het onderwijs wel past. [morgen verder]

unroll @threadreaderapp

Toch was die kritiek er al vrij snel. Zowel A.D. de Groot als Bob van Naerssen kwamen al snel na publicatie van het door hun geredigeerde en sterk ideologisch gekleurde 'Studietoetsen construeren, afnemen, analyseren' (Mouton, 1969) tot een radicaal andere standpunt waarin juist

de positie en het belang van de LEERLING voorop stond. De psychometrie heeft maling aan de leerling. De psychometrie is sterk in zichzelf gekeerd met zijn streven om vergelijking van leerlingen een wiskundige orm te geven. Er is nog gelegenheid genoeg om daarop door te gaan.

De Groot publiceert in 1970 een pleidooi om aan de typische kwaliteitseisen uit de psychometrie een overkoepelende eis toe te voegen: toetsen moeten door leerlingen doeltreffend zijn voor te bereiden. benwilbrink.nl/publicaties/70… Laat dat 'doeltreffend' even inzinken. Het betekent:

geen geheimzinnigheid over wat hoe zal worden gevraagd, en waar de grens voor een voldoende zal liggen. Tien jaar later zou er aan de UvA gedoe ontstaan over het geheim houden van tentamenvragen. Veertig jaar later over geheimhouden door het CvTE van #rekentoets-vragen.

In feite eist De Groot dat leerlingen tevoren een goede inschatting moeten kunnen maken van het resultaat dat zij op de toets zullen halen. Dat is immers een noodzakelijke voorwaarde voor een doeltreffende voorbereiding. Bob van Naerssen was medewerker van De Groot, en hield

in 1970 zijn inaugurele rede als lector over wat hij een 'tentamenmodel' noemde. Een toetsmodel dus ook. benwilbrink.nl/publicaties/70… De titel is veelbelovend: 'Over optimaal studeren
en tentamens combineren'. Het gaat over de constructie van een wiskundig model voor het opstellen

van een verwachte score op het nog af te leggen tentamen. Ik zeg het iets anders en simpeler dan hoe Van Naerssen zijn model presenteert; ik heb daar mijn redenen voor, kom er nog op terug. Punt is: Van Naerssen geeft een wiskundige uitwerking van het idee van De Groot.

We zijn ondertussen meerdere stappen verwijderd van het idee 'meten is weten'. Maar het is puur winst, want De Groot en Van Naerssen geven aandacht en inhoud aan de CONTEXT van het proefwerk/tentamen/examen. In het onderwijs is een beoordeling een resultaat waarop is gestuurd.

Ho, maar wacht even. Wat is dat voor fenomeen, een meting doen waarop willens en wetens is gestuurd? Wat 'meten' we dan? Kijk, nu komen we ergens. Studieresultaten kunnen we niet goed duiden zonder te weten hoe leerlingen zich hebben voorbereid, welk cijfer ze wilden halen.

Ik kan dit het best duidelijk maken aan de hand van de analyse van een kleine set gegevens uit onderzoek van Sem Everwijn en Ton Willemsen, over o.a. tijdbesteding in de voorbereiding, en behaalde scores. Zie hier: benwilbrink.nl/publicaties/77… (paper voor Onderwijsresearchdagen 1977).

Het paper presenteert een heuristisch model om over de duiding van (verschillen tussen) toetsscores van gedachten te kunnen wisselen. Ivo Molenaar was er destijds enthousiast over (opsteker). Wat toetsscores betekenen hangt immers af van hoe zij tot stand zijn gekomen.

Hoe komen zij tot stand: de leerling neemt meer/minder voorkennis mee, heeft een bepaalde ambitie ('6' is wel voldoende, het moet echt een '9' worden), besteeds meer/minder tijd aan de doeltreffende voorbereiding. Dit klinkt ingewikkeld, maar zie, er is een aardig wiskundig

model voor dat gebruikt maakt van de bijzondere afhankelijkheden tussen de vier variabelen: de score is mede afhankelijk van de voorkennis, maar niet omgekeerd, enzovoort. Wie een geschikte dataset heeft verzameld, kan de oorzakelijke verbanden dan uitrekenen.

Dezelfde eindscore kan op veel verschillende manieren zijn bereikt, of worden bereikt. Dat heeft betekenis voor het onderwijs. En natuurlijk ook voor de duiding van de eindscore zelf.
Wat betekent het wanneer de hele klas laag scoort? Heeft de leraar daar aanwijzingen voor?

Prangende vragen zijn er uiteraard in de overgangsvergadering. Wat betekenen de cijfers voor de leerlingen in de gevarenzone? Wat weten we over die leerlingen? Want de overgangsregeling botweg toepassen op de genoteerde cijfers is niet toelaatbaar, dat weet iedereen, toch?

Wanneer de betekenis van de toetsresultaten afhangt van andere gegevens zoals voorkennis, streefniveau en tijdbesteding — en dat is altijd het geval — dan levert de toets dus onvolledige meetgegevens op, zou je kunnen zeggen. Meten is onvolledig weten.

Zo is het van belang enig inzicht te hebben in de mate waarin leerlingen erin zijn geslaagd zich doeltreffend op het proefwerk of welke beoordeling dan ook, voor te bereiden. Verschillen tussen streefniveau en behaald resultaat geven daar aanwijzingen voor. Het model helpt dit

soort vragen te stellen. Het tentamenmodel van Bob van Naerssen helpt om maatregelen te vinden die belemmeringen voor een doeltreffende voorbereiding (De Groot) uit de weg kunnen ruimen. We zijn dan met zijn allen niet meer bezig met meten, maar met het onderwijs optimaliseren.

Als leerling je toetsscore voorspellen.

Dan is het nu tijd om ons te realiseren dat een toets geen meetinstrument is, maar een STEEKPROEF uit wat de leerlingen weten en kunnen. Laten we, met De Groot en Van Naerssen, de situatie bekijken met de ogen van de leerlingen.

Iedere toets ziet er voor de leerlingen uit als een steekproef uit alle mogelijke vragen over de opgegeven leerstof. Lees het nog een keer, alsjeblieft. Want het standpunt van de leerling kiezen is echt heel bijzonder, en biedt een volkomen ander vertrekpunt dan de psychometrie.

Bob van Naerssen pleitte dan ook voor een DIDAKOMETRIE die aansluit bij wat er voor het onderwijs nodig is. Van Naerssen was waarschijnlijk de eerste Nederlandse psycholoog die een besliskundige benadering koos bij selectieproblemen. In casu: chauffeurs in de landmacht, zijn

proefschrift. Een besliskundige benadering drukt je met de neus op de vraag: beslissingen VAN WIE? Bij onderwijs schieten we meteen in de reflex: de leraar, natuurlijk. Maar bij nadere beschouwing is dat niet helemaal correct: de LEERLING neemt voortdurend beslissingen.

Dit is in het basisonderwijs minder vanzelfsprekend dan in het voortgezet onderwijs. Oké. De uitdaging voor leraren is de leerlingen te helpen om handige beslissingen te nemen, om proefwerken goed voor te bereiden. De hamvraag daarbij is: kan de leerling zijn toetsscore

voorspellen? Dit is echt wel een lastige vraag, want het is niet zo dat de meeste leerlingen voor de meeste proefwerken tienen scoren. Oké, bent u dat met mij eens? Ik ga proberen u mee te nemen op een korte ontdekkingsreis naar het antwoord.

Ik neem u mee in een gedachte-experiment. Stel u bent een leerling die net zijn proefwerk heeft teruggekregen: 60 % van de vragen waren goed, de overige fout. Als u nu een nieuw proefwerk zou mogen maken, wat is uw verwachte score? Simpel, ook 60% natuurlijk. 'No-brainer'.

Maar niet PRECIES 60%, hè! Het kan ook meer zijn, of minder. Kunnen we dat helder krijgen? Jawel hoor, volg de logica. Wat is de kans dat je (je bent nog steeds die leerling) de eerste vraag goed beantwoordt? Precies, die is 0,6; het is voor jou immers een willekeurige vraag.

Wat is de kans voor de tweede vraag? Aha, ook 0.6. Je hebt het door: voor alle vragen, zeg dat het er 20 zijn, is de kans op een goed antwoord 0.6. De kansverdeling voor de toets van 20 vragen is dan de binomiaalverdeling, zie Wolfram wolframalpha.com/input?i=binomi…

Dus ja, de voorspelling is 60%, dus 12 goed uit 20, maar jeetje, het kan ook zomaar 9 zij, of 15. Eigenlijk had ik u eerst moeten vragen zelf een schets te maken van hoe u denkt dat de verdeling eruit ziet. Het is eigenlijk een histogram.

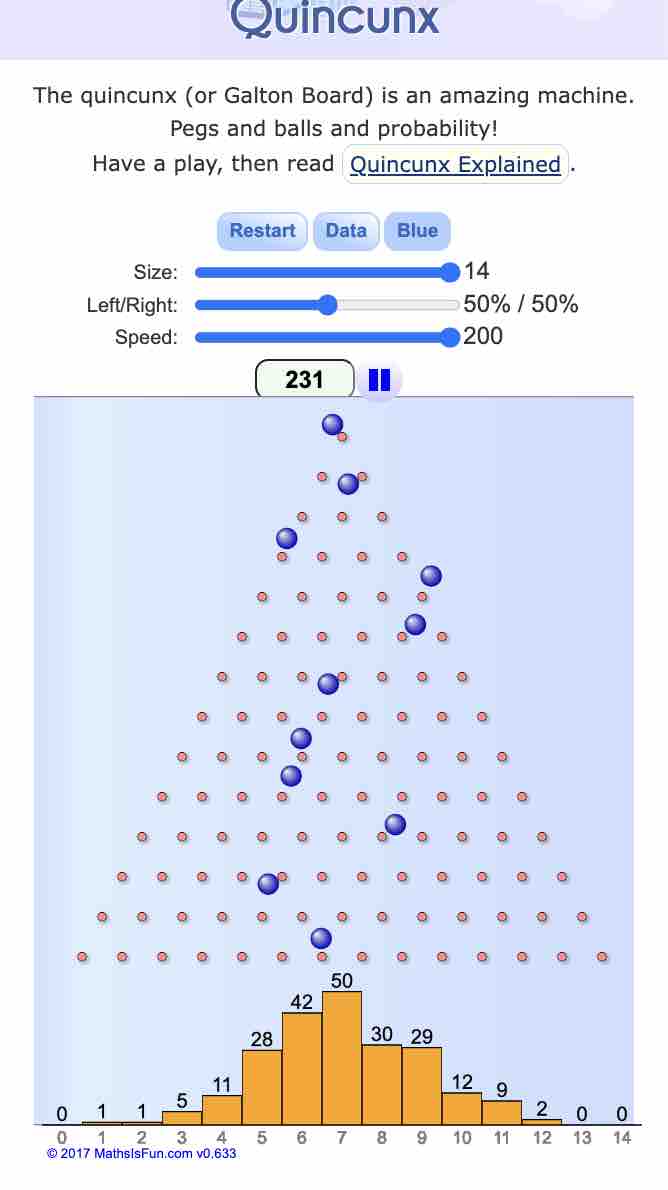
Een ook historisch interessant instrument om die binomiaalverdeling te simuleren is de quincunx van Sir Francis Galton: mathsisfun.com/data/quincunx.… . Speel er wat mee. Het maximum aantal 'toetsvragen' is 14 (van boven af), daar moeten we het mee doen. Stel kans 0,6 in als 40%/60%.

Bij ieder pinnetje op zijn weg naar beneden is de kans op 'naar rechts' 0,6, naar links 0,4.
Het is een ongelooflijk krachtig model, zowel de binomiaalverdeling, als zijn materiële maar hier digitale vorm van de quincunx. Volg de logica nog eens terug, en laat het rustig tot

u doordringen dat een leerling die 60% van de stof beheerst, gerekend naar het percentage vragen dat hij goed zou beantwoorden, een groot risico loopt op een echt lagere score dan die 60% op een steekproef van 20 vragen, maar ook een grote kans op een fors hogere score.

In de psychometrische testliteratuur zoals de klassieke tekst van Frederic M. Lord and Melvin R. Novick (1968). 'Statistical theories of mental test scores', gaat alle aandacht uit naar wat de leraar op basis van gerealiseerde scores kan zeggen over de 'ware' stofbeheersing.

Maar wat heeft de leerling aan platonische oefening over 'ware stofbeheersing'? Niets. Het gaat de leerling, en trouwens ook de leraar, om het resultaat. De score. Daar krijgt de leerling een cijfer voor, en dat telt. En dan laat de quincunx zien dat die score deels TOEVAL is.

Het laat zich raden dat de binomiaal als model voor de score op toetsen slechts het begin is van het modelleren van toetsen en examens. De binomiaal gaat uit van een specifieke waarde voor de ware stofbeheersing, maar die ware stofbeheersing kennen we slechts bij benadering.

De psychometricus construeert dan een betrouwbaarheidsinterval voor die ware score voor de hele groep leerlingen, en doet daar vervolgens niets mee. In een tentamenmodel is de toetsscore van een individuele leerling de basis om een kansverdeling ('likelihood') voor zijn ware

stofbeheersing op te stellen. Ik ga dit niet verder toelichten. Wie nieuwsgierig genoeg is, zie voor de verdere uitwerking benwilbrink.nl/projecten/spa_… [Ik heb werk aan het model gestaakt bij ernstige problemen met de veiligheid van JAVA, helaas. De applets zijn buiten werking.]

De doeltreffendheid die A.D. de Groot als belangrijkste kwaliteitseis stelt, valt uiteen in
(1) een inhoudelijke eis: het wat en hoe van de vragen in de toets, en
(2) een strategische eis: de leerling moet inzicht hebben in het risico van een te lage score.

(1) betekent dat vragen in een summatieve toets niet moeilijker of anders zijn dan de vragen die in het voorafgaande onderwijs zijn behandeld en geoefend.
Is dat een verrassing voor u? Mooi, dan heb ik een punt gescoord.

(2) als de toets inhoudelijk overeenstemt met het gegeven onderwijs (een 'integere toets'), dan heeft de leerling best wel een goed idee over de te verwachten score op de toets. Maar daarmee nog niet over risico om te zakken. Ik ga het nog over cijfers hebben. [Morgen dus]

Nota Bene. De score op een toets of examen is deels toeval, want het resultaat van de vragen in de toets, een set vragen die even goed een heel andere had kunnen zijn. Dat is een wezenlijk verschil met metingen: die zijn niet toevallig, maar hebben wel een mogelijke meetfouten.

Een deels toevallige score op een toets of examen is geen meetfout: er gebeurt niets dat ongewenst is.
Dat inzicht moet gevolg hebben voor de taal waarin we vaak spreken over beslissingen op basis van examens, of selectieve tests: dat die 'terecht' of 'onterecht' kunnen zijn.

Maar dat is niet zinvol. De beslissingen zijn wat ze zijn. Ze zouden anders zijn geweest, wanneer 'paralleltoetsen' waren gebruikt: in alle opzichten gelijkwaardig, maar met andere vragen.
Laten we ons voornemen wendbaar te denken bij het beoordelen in het onderwijs.

Aan welke knoppen kan de leraar draaien?

Het aandeel van toeval bij toetsen en examens is zo groot dat er maatregelen genomen moeten worden om er goed mee om te gaan. Allereerst inhoudelijk: door voortdurend te werken aan verbetering van de kwaliteit van de toetsvragen zelf.

Hoewel dit direct de 'meetkwaliteit' van toetsen raakt, wil ik dit spoor hier niet verder volgen. Ik schreef begin 80er jaren een kursusboek over het ontwerpen van toetsvragen (Aula 809), zie een uitgebreide en herziene tekst hier benwilbrink.nl/projecten/toet….

Een interessante knop om aan te draaien is: stel korte tijd voor een belangrijk proefwerk een oud proefwerk af, als proeftoets. Dat geeft leerlingen een laatste waarschuwing, mochten zij een verkeerd idee hebben over hoe goed ze zijn voorbereid. De kwantitatief ingestelde

leraar kan op basis van de proeftoetsscores de slaagkansen voor het echte proefwerk berekenen (het SPA-model benwilbrink.nl/projecten/spa_…).
Een directe ingreep om aandeel van het toeval te verminderen is, u raadt het al: de toets verlengen. Meer vragen opnemen in de toets.

Maar toetsen verlengen kan niet onbeperkt hè!
Een interessante knop waaraan gedraaid kan worden: maak de toetsvragen minder moeilijk. Er zijn een aantal redenen waarom onze toetsen vooral MOEILIJK zijn. (1) Een eeuwenoude traditie om prijzen te geven aan de beste leerlingen:

J. Spoelder (2000). 'Prijsboeken op de Latijnse school: een studie naar het verschijnsel prijsuitreiking en prijsboek op de Latijnse scholen in de Noordelijke Nederlanden, ca. 1585-1876'. Dissertatie. open: repository.ubn.ru.nl/handle/2066/14… Pas op: 100 Mb.

Om daar geen conflicten over te krijgen, moest er natuurlijk wel een duidelijke afstand zijn tussen de nummer 1 en de nummer 2, enzovoort. Dus lastige opgaven opgaven stellen.
(2) In het moderne onderwijs, met de oprichting van H.B.S. zeg maar, oefenden leraren een sterke

selectieve druk uit op hun leerlingen, resulterend in tamelijk vaste percentages zittenblijven/afstromen van circa 23% JAARLIJKS. K. Posthumus schreef er een fel stuk over in De Gids van 1940 dbnl.org/tekst/_gid0011…

Na WOII is dat percentage van 23 iets teruggelopen, en vervolgens hoog gebleven, ook ondanks de mammoetwet. A.D. de Groot heeft de vooroorlogse jaren nog meegemaakt, mogelijk heeft dat hem ook gemotiveerd tot het schrijven van zijn 'Vijven en zessen' (niet online). In dat boek

schenkt hij ruim aandacht aan het fenomeen dat docenten wis- en natuurkunde door moeilijke proefwerken en strenge cijfers zichzelf belangrijk konden maken t.o.v. leraren van andere vakken.
(3) Je zou denken dat De Groot met zijn studietoetsen dan een tegenwicht zou willen

bieden, maar dat was althans in 'Studietoetsen' van 1969 nog niet het geval: dat boek beveelt aan om toetsvragen een moeilijkheid van rond de 0,7 te geven. Dat berust op het psychometrisch denken dat je dan de grootste spreiding tussen leerlingen kunt krijgen. Alsof dat

verdorie een onderwijsdoel zou zijn. Vreselijk.
Waarom zou er in (1), (2) en (3) een gerede grond zijn om door te gaan met toetsvragen die vooral MOEILIJK moeten zijn om zo onderscheid tussen leerlingen te kunnen maken? Dit is ook een ethische kwestie hè! Houd ermee op.

Met makkelijke toetsvragen wordt het aandeel van toeval in de uitslag op de toets kleiner. Gebruik die knop dus. Dat wil overigens niet zeggen dat het daarmee ook makkelijker wordt een 'voldoende' te scoren: moeilijkheid van toetsvragen en van de toets zijn verschillende zaken.

Ik stip hier ook maar even aan dat minder moeilijke vragen in de toets ook betekent dat in het onderwijs zelf minder moeilijke vragen worden gebruikt. Dat heeft alleen maar didactische voordelen, vermoed ik.
Kwestie van testeffect, lees de blog van David learningspy.co.uk/english-gcse/w…

Kort door de bocht komt het erop neer dat het de leerling bij makkelijke vragen meestal lukt om de informatie op te halen uit de grijze hersencellen. Deze activering van het herinnerde consolideert die kennis ook weer. Geweldig voordeel van makkelijke vragen boven moeilijke.

Ik las hier een pauze in. Over knoppendraaien ga ik nog een vervolg schrijven, want het toeval bij afzonderlijke toetsen blijft ondanks alles groot. Maar let op, het is mogelijk toetsen enorm te 'verlengen' door meerdere toetsen te combineren. Klinkt dat bekend? Leuk hè!

Ik maakte eerder tussen neus en lippen door een belangrijke opmerking: De dominante psychometrische benadering ziet toetsen als iets met groepen en dus verschillen tussen leerlingen. Terwijl de didakometrie van Van Naerssen begint bij de individuele leerling.

De psychometrische aanpak maakt veel werk van de moeilijkheid van vragen, hun 'p-waarde'. De aanname die zelden expliciet wordt gemaakt, laat staan ter discussie gesteld: vragen die iedereen goed kan beantwoorden hebben geen onderscheidend vermogen en horen niet in een toets.

Maar daar kijkt iedere leraar dwars doorheen, toch? Wat is dit voor depressieve benadering van onderwijs? Dan hébben je leerlingen de stof goed onder de knie, en dan zou je geen toetsvragen mogen gebruiken die dat dan ook vaststellen? Zo bizar is, echt waar.

In de psychometrische aanpak zijn de p-waarden van de toetsvragen belangrijk, en die p-waarden zijn GROEPS-statistieken. Ze worden berekend op basis van de antwoorden die de HELE KLAS heeft gegeven.

De didakometrische aanpak gaat uit van de beslissituatie van de leerling die zich voorbereidt op summatieve beoordeling. De basis voor een passend wiskundig model daarvoor is het binomiale proces: gegeven een stofbeheersing van bijvoorbeeld 80%, is de kans een willekeurige

vraag goed te kunnen maken 0,8. Die 0,8 noemen we ook p = 0,8, maar dit is NIET de moeilijkheid van de vraag zoals die blijkt bij klassikale afname. De klassieke psychometrische p-waarde van toetsvragen is een totaal ander begrip dan de kans p op een goed antwoord in het

didakometrische binomiale model. Voor wie is opgevoed met het idee dat iedere toetsvraag een karakteristieke moeilijkheid p heeft is dit laatste moeilijk te bevatten. De p-waarde van een toetsvraag is een antwoord op een totaal ander probleem dan dat van transparantie van de

toets voor de leerling die zich erop aan het voorbereiden is.
Natuurlijk, ook die leerling gaat in de toets vragen tegenkomen die IN DE KLAS door velen fout worden gemaakt, of door bijna iedereen goed, maar dat is kennis achteraf. Van achteren kijk je de koe in de kont.

Onthoud dit onderscheid tussen p-waarde als groepsstatistiek en de kans p dat een leerling het antwoord op de eerstvolgende vraag weet. Het is verdomde belangrijk.
Het mag ook duidelijk maken dat het 'meten is weten' van de psychometricus de individuele leerling niet helpt.

En wat de individuele leerling niet helpt, helpt ook de klas niet, ook de leraar niet.
Er is, wat 'meten in weten' betreft dus een groot verschil tussen toetsen die het Cito en andere partijen op de markt brengen, en de toetsen die je als leraar zou willen inzetten.

Toetsen combineren. Bij examens, en natuurlijk ook bij overgangsbeslissingen. Het gaat om beslissingen die voor de leerlingen van groot belang zijn. Meestal zijn er een behoorlijk aantal toetsen als beschikbare prestatiegegevens. Hoe al die informatie optimaal te combineren?

Ik herinner aan de titel van de rede van Bob van Naerssen: 'Over optimaal studeren
en tentamens combineren.' Er zitten meerdere kanten aan deze examenkwestie. Allereerst: toetsen zijn zwakke 'metingen', zoals ik in deze draad heb laten zien, maar tel ze op: dat is sterke info.

Ga geen ruzie maken met collega's over het belang van het eigen vak, dat je met een onvoldoende voor jouw vak niet over zou kunnen gaan. De eerste stap bij optimaliseren van de overgangs- of examenregeling is: tel alle resultaten bij elkaar op.

Het onderwerp 'hoe toetsen te combineren' is te uitgereid om hier verder te behandelen. Ik heb dat in 1917 wel gedaan, voor propedeutische examens met een BSA (Bindend StudieAdvies): 'Compenseren in examens', voordracht voor de HES: benwilbrink.nl/publicaties/17…

Het gaat daar naast het optimaliseren van de combinatie van toetsen als 'meting', ook om het optimaliseren van de examenregeling vanuit het doel alles zo transparant (De Groot) mogelijk te maken. Bij een BSA moet immers iedere student binnen dat eerste jaar kunnen slagen.

Onderling compenseren van toetsen/vakken heeft al een halve eeuw mijn warme belangstelling, omdat het onnodig zittenblijven en overdoen voorkomt. Kwestie van doelmatigheid, gaat over enorme bedragen hoor.

Ik maak voor die combinatie-problematiek ook weer gebruik van wiskundige modellen, die voortbouwen op het binomiale model voor afzonderlijke toetsen. De vele figuren zijn geplot met hulp van eigen software. (Java programmatuur, gebouwd met BlueJ; niet online, maar vraag mij).

Dan nu dat andere onderwerp dat voortdurend over deze beschouwing heen zweeft: cijfers, en cijfergeven.
Merk op dat toetsscores het fundament vormen: zijn antwoorden goed of fout. Cijfers zijn waardeoordelen over de prestaties. En zelf weer de basis voor cesuren (on)voldoende.

Hét boek over cijfers en cijfergeven waar iedereen wel van heeft gehoord is 'Vijven en zessen' van A.D. de Groot, uit 1966. Ik heb Adriaan eens gevraagd of hij iets wist van de geschiedenis van dat cijfergeven. 'Goede vraag', vertelde hij, 'ik heb er geen moment aan gedacht!'

En toch moet er een interessante geschiedenis zijn, want tot eind 19e eeuw was rangordenen de meest gebruikte truc om leerlingen achter de vodden te zitten. Ik heb er ook nog een staartje van meegemaakt, ik was in de 1e klas (1950) 12/30, 6/29 en 7/29, daarna geen rangordes meer.

Interessant detail is dat het aantal leerlingen in de klas erbij is vermeld.
Ooit is het lichamelijk of geestelijk bestraffen van fouten vervangen door een humaner methode van de beste studenten te belonen, soms met een baan of prebende, later vaak met prijsboeken. Daarvoor

moest er iets van een puntentelling zijn, om een rangorde te kunnen vaststellen. Over rangordenen op zich zijn ook weer boekwerken verschenen, het levert interessante statistische problemen, en maatschappelijke spelletjes van allerlei aard.

Amy N. Langville & Carl D. Meyer (2012). 'Who's #1? The Science of Rating and Ranking' press.princeton.edu/titles/9661.ht… Hoofdstuk 1 is vrij: assets.press.princeton.edu/chapters/s9661…

Nummer 1 van de klas zijn is mooi, maar als dat een klas van 3 leerlingen is (op veel Latijnse scholen in eeuwen van lamlendigheid het geval) is dat iets anders dan nummer 1 van een klas van 30. Klassen verschillen ook: het ene jaar is evident 'beter' dan het andere. Soms

zijn verschillen tussen leerlingen nihil, dan weer groot. Kortom, er was ook onvrede over die rangordes. In de 19e eeuw, de eeuw van tellen, meten en standaardiseren, werd er dus gewerkt aan of gezocht naar alternatieven. Over de Franse 'Agrégation' is bekend

(André Chervel (1993). 'Histoire de l’Agrégation. Contribution à l’histoire de la culture scolaire' blz. 136 e.v.) dat de juries stapsgewijs het rangordenen vervingen door cijfergeven. Mogelijk is hetzelfde op meerdere plaatsen gebeurd, maar ongetwijfeld hebben de meeste

scholen het rangordenen in een keer vervangen door cijfergeven, gezien voorbeelden in andere scholen. Leerlingen van het Gronings gymnasium moesten veel geduld hebben: de rector gruwde van de nieuwigheid, maar bereikte een zeer hoge leeftijd in functie. In 1903 was het gedaan.

Het is niet alleen maar leuk en aardig hier even bij stil te staan. Deze geschiedenis laat immers zien dat ons cijfergeven een poging is het oude rangordenen te standaardiseren. Cijfergeven is nog steeds rangordenen. Zij het gestileerd, als nep-standaardisatie. Het is bedrog.

Een bekendere zienswijze op dat cijfergeven is dat het een vorm van RELATIEF beoordelen is: in geen velden of wegen zijn er ABSOLUTE normen voor te bekennen. Laat het ons enigge nederigheid leren bij ruzies die we maken over vijven en zessen.

Dat cijfergeven heeft niet veel meer met 'meten' te maken. Oké, rangordenen is ook een vorm van meten, pseudo-gestandaardiseerd of niet.
Anders dan Engelse cijfersystemen brengt de Nederlandse gewoonte een '5' net 'onvoldoende' te vinden veel problemen mee. Volgend onderwerp!

Onderwijs is een fenomeen van alle tijden. Beoordelen van leerlingen dus ook. Overzichten daarvan zijn zeldzaam. Ik schreef zelf een historisch overzicht, als 'appetizer' voor een proefschrift over toetsen, doe er uw voordeel mee: benwilbrink.nl/publicaties/97…

Heb ik verteld dat juf Dronkers (1e klas, met groen leren jack en helm op de bromfiets naar school) haar kinderen dus ook op volgorde van die rangnummers in de bankjes zette? De 'besten' links voor in de klas. De keerzijde daarvan: de 'slechtsten' rechts achter in de klas.

Mijn oude rapportboekje bevat nog een interessant gegeven, tot mijn verrassing: naast mijn eigen cijfers ook het gemiddelde cijfer van de klas (2e, 3e, 4e en 5e klas). Ik maak er een bestandje van. Dit zijn dus gemiddelde rapportcijfers van dezelfde 'jaargroep'.

Het is allemaal erg vlak. Dat is wel te verwachten met gemiddelden, maar dit is wel érg vlak hoor. Dit beeld zal best representatief voor het cijfergeven in Nederland zijn. Twee uitbijters: gymnastiek (gymleraar daarvoor) en klas 5 (leraar was nieuw op school, hij begon streng).

De cijferschaal loopt van 1 tot 10, ruimte zat voor variatie. Toch komen al die gemiddelden uit op 'iets rond de 6,5'. Ik vind het een bijzonder fenomeen. Kunnen we zeggen dat het 'metingen' zijn? Er zit eigenlijk geen informatie in, behalve dat er geen informatie in zit.

De informatie van de gegeven cijfers zit verborgen achter die gemiddelden: er is natuurlijk een behoorlijke spreiding TUSSEN de leerlingen van deze jaargroep. Een rangorde dus. Het lukt de onderwijzers prima om te rangordenen, maar daar zijn ze toch niet voor aangesteld?

En waarom liggen die gemiddelden rond 6,5? Dat is simpel, een 6 is 'voldoende', een 5 is 'twijfelachtig', zoals mijn rapport het benoemt. (Aan plusjes of minnetjes, of halve punten, deed mijn school niet). Die cijfers en hun betekenis waren overigens wettelijk verankerd.

Daar zou nog eens een historisch onderzoekje op uitgevoerd kunnen worden. Mogelijk is de wet van Thorbecke voor de H.B.S. de eerste die de cijferschaal wettelijk vastlegt. Een curieus feitje (de bron moet ik nog eens zien te achterhalen):

Onderwijsminister Gerrit Bolkestein veranderde (vlak voor WOII) de betekenis van de '5' van 'juist voldoende' naar 'juist onvoldoende'. Het is wel bijzonder dat de wetgever zich in deze mate van detail bemoeit met zoiets subjectiefs als schoolcijfers en hun betekenis.

Gerrit Bolkestein was niet de enige. Marja van Bijsterveldt gaf de examencijfers voor 'kernvakken' een bijzondere betekenis, nog nooit eerder vertoond. Daar kwam later nog een oekaze bij dat gemiddelde cijfers voor het schoolexamen niet meer dan een half punt mogen afwijken

van die voor het centraal eindexamen. Bizar. Het idee achter dit soort ingrepen is wel duidelijk: 'de lat moet omhoog'. Maar dat doe je niet door de betekenis van cijfers te veranderen: dat heeft een kortstondig effect, daarna is het oude evenwicht snel weer hersteld.

Dergelijke maatregelen van de wetgever hebben dus geen positief effect op onderwijsresultaten, maar ze maken het leven voor iedereen wel een stuk moeilijker. Met cijfers kan er dus behoorlijk worden gerotzooid. Afijn, ik dwaal af.

We hebben dus onderwijswetten die vastleggen dat cijfers in twee kwaliteiten komen: voldoende cijfers, en onvoldoende cijfers. Er zijn er die geen scherpe grens willen tekken, en een 5 'twijfelachtig' noemen, maar bij Gerrit Bolkestein is dat dus 'nipt onvoldoende'.

Het probleem met deze cijferschaal waar een 5 al 'nipt onvoldoende' is: er zijn wel heel erg veel gradaties van 'onvoldoende'. Dat is op zich al gekkigheid genoeg, maar ernstiger is de gewoonte om cijfers niet als ranggetallen te beschouwen, maar als liggend op een

ratioschaal. Wat is een ratioschaal: daar is een 10 twee keer zo goed als een vijf. Een 4 is half zo goed als een 8. Waarom doen leraren als cijfers ratio-getallen zijn: omdat ze vinden dat cijfers gemiddeld mogen worden, bijvoorbeeld tot rapportcijfers. Nou, vooruit, we

kunnen met zijn allen afspreken dat we het zo blijven doen, ook al weten we dat het eigenlijk niet klopt. Daar is toch niets mis mee? Toch wel. Omdat cijfers stug gemiddeld worden, is een stevige onvoldoende een godsoordeel waar je als leerling moeilijk nog overheen komt.

Daarom gooi ik er een stelling in:

het is misdadig om gebruik te maken van het lage deel van de cijferschaal, zeg de cijfers 1 tot en met 3, mogelijk 4.
Misdadig, omdat het geestelijke mishandeling van leerlingen is. Het tast direct hun recht op onderwijs aan. Ophouden ermee.

Een ethiek of beroepscode voor beoordelen in het onderwijs zou dit probleem glashelder moeten behandelen.
Voor het voortgezet onderwijs is er wel een model voor zo'n code ontwikkeld (1998), wist u dat? benwilbrink.nl/projecten/toet…

Volgens de meeste overgangs- en examenregelingen moetn zware onvoldoendes ergens worden gecompenseerd door hoge cijfers voor hetzelfde of soms een ander vak. Maar compenseer maar eens een 3! Of een 1 die om duistere redenen is uitgedeeld.

Los van de ellende van absurd lage cijfers, voltrekt zich voortdurend een stille en dus onbegrepen ramp met cijfers in de buurt van de grens tussen voldoende en onvoldoende. Of dat nu op afzonderlijke toetsen is, of voor overgangs- en examenbeslissingen.

Ik heb nog eens 12 jaar schoolrapporten van mij zelf en enkele van mijn echtgenote doorgebladerd. Mijn god Ciska, het lijkt wel of die rapportcijfers door een aantal chaoten zijn uitgedeeld. Waar duidt dat op?

(1) Kennelijk lukt het leerlingen niet om consistent te presteren, ook al zijn rapportcijfers het gemiddelde van enkele of meerdere proefwerken / toetsen / beurten / whatever.

(2) Kennelijk zijn de toetsen te onbetrouwbaar om zelfs bij het middelen van proefwerkcijfers een behoorlijk beeld van de kennis van de leerlingen te geven.

(3) Kennelijk vormen de rapportcijfers eerder momentopnamen, dan dat zij een beeld van de kennis en kunde van de leerlingen geven.

(4) Kennelijk zitten de leraren ook met de handen in het haar, hebben zij het idee dat ze voor hun leerlingen zo ongeveer de hele cijferschaal moeten gebruiken, maar zijn de werkelijke verschillen tussen leerlingen te klein om dat op te kunnen verantwoorden.

Zegt u het maar. De willekeur zit over de hele cijferschaal, ook bij de hoge cijfers. Maar voor de meeste leerlingen zijn er voortdurend onzekerheden in de buurt van de grens voldoende-onvoldoende. Wat doen we onze leerlingen aan met die permanente selectieve druk?

A.D. de Groot had moeite met die grens voldoende/onvoldoende, want hij zag ook wel in dat er geen INHOUDELIJKE argumenten zijn om op puntjes verschil ofwel een voldoende uit te delen, ofwel een onvoldoende. In methodologie-jargon: beslissingen rond die grens zijn niet valide.

Je zou ook kunnen zeggen: leerlingen kunnen zich niet doeltreffend op toetsen voorbereiden (De Groot, 1970) wanneer zij met een goede voorbereiding toch een stevig risico op een onvoldoende hebben. En zo is het.

Er is wel een cynische oplossing voor het door De Groot gesignaleerde probleem. Die oplossing ziet het vijven en zessen als een onvermijdelijk probleem (maar dat is het natuurlijk niet), en waarschuwt leerlingen dat ze in hun onderwijsloopbaan vaak onvoldoendes zullen scoren.

It's part of the game. Leraren kunnen proberen de schade te beperken, door zo transparant mogelijk te zijn.
Een voorbeeld van een waarschuwende aanpak is het projekt 'Schriftelijke raad ex art. 24bis' bij Rechten aan de UvA, eind 80er jaren. Zie bv. benwilbrink.nl/publicaties/87…

In deze beschouwingen gaat het voortdurend om de mogelijke gevolgen die toetsresultaten hebben. 'Meten is weten' als one liner voor toetsen schiet hier dus schromelijk tekort. Het 'meten' moet de beslissingen die erop volgen, kunnen dragen. In beginsel is dat een empirische

kwestie: het moet worden onderzocht. Het is niet dat leraren daar voortdurend mee bezig moeten zijn, maar laten we met zijn allen wat meer 'evidence informed' gaan werken. Ook al is dat verre van eenvoudig, want voor het laten overdoen van toetsen, tentamens, klassen, en

examens is zelfs een theoretische onderbouwing vaak ver te zoeken, laat staan een empirisch getoetste.
Een besliskundige aanpak van deze 'overdoen'-problemen heb ik in 1980 geschetst in het Tijdschrift voor Onderwijsresearch. Voor de liefhebbers:

'Optimale Criterium-Gerefereerde Grensscores zijn Eenvoudig te Vinden' benwilbrink.nl/publicaties/80… en 'Enkele Radicale Oplossingen voor Criterium-Gerefereerde Grensscores' benwilbrink.nl/publicaties/80…
De titels heb ik zelf bedacht, mogelijk beloven ze meer dan ik heb waargemaakt, haha.

Ik denk deze draad te gaan afsluiten met deze stelling aan werk van James Coleman:
H
eel dat cijfergeven speelt zich af als een stilzwijgende onderhandeling tussen de twee betrokken partijen, de leerlingen en hun leraren.

'Vijven en zessen' in een toetsbaar wiskundig model.

De grondgedachte is tamelijk simpel. Leerlingen investeren hun tijd in voorbereiding op de toets, en krijgen daar cijfers voor terug. Leraren hebben cijfers om uit te delen, en krijgen daarvoor de tijd die leerlingen aan de voorbereiding willen besteden. Capito? Lees het 2x.

Er zit dynamiek in. Het is armpje drukken tussen leerlingen en leraren. Vanwege die dynamiek zijn de gewone sociaal-wetenschappelijke technieken van data-analyse niet bruikbaar. James Coleman biedt in zijn (1990) 'Foundations of social theory' een klasse wiskundige modellen

die onze 'onderhandeling' aankunnen. hup.harvard.edu/catalog.php?is… Welke gegevens zijn er nodig om dit te kunnen onderzoeken? Ha, die zijn we eerder al tegengekomen: bij de leerlingen zijn dat hun voorkennis, streefniveau (welk cijfer mik je op?), tijdbesteding en behaalde cijfers.

De leraren hebben die cijfers uitgegeven, hebben de toetsen afgenomen, en waren verantwoordelijk voor de relevante omstandigheden bij de voorbereiding op de toetsen (transparantie, De Groot 1970). In het meerjarig project 'schriftelijke raad ex art. 24bis' bij Rechten UvA zijn

precies die data verzameld. Ik heb het passende wiskundig model van James Coleman erop kunnen toepassen. Zie het paper uit 1992 'The first year examination as negotiation' benwilbrink.nl/publicaties/92… De gelegenheid heeft mij ontbroken dit onderzoek behoorlijk te publiceren.

Dat is jammer, want het onderzoek heeft inderdaad laten zien dat de twee betrokken partijen elkaar stevig in de houdgreep hebben. De suggestie die hiervan uitgaat is dat het verdraaid lastig zal zijn voor een van de partijen, zeg dat het de leraren zijn, om de ban te breken.

Onze schoolse toetscultuur is ijzersterk geworteld in een overigens door weinigen begrepen traditie van 'zo doen we dingen altijd al'. Ik hoop dat maar dat baanbrekend werk zoals van James Coleman inzicht in die tradities kan geven. Ik heb aan dit conferentie-paper ook

een korte briefwisseling met James Coleman gehangen.
Ik weet niet of ik met deze korte aantekeningen over die onderhandeling tussen leerlingen en leraren mijn gevoel over heb kunnen brengen dat hier alles zo'n beetje samenkomt wat in het voorgaande is behandeld over

het tekort van de slogan 'meten is weten'. Ook de didakometrie waar Van Naerssen voor pleitte, vindt hier een natuurlijke plaats. Die didakometrie kiest allereerst het standpunt en ook het belang van de leerling die zich voorbereidt op toetsen. De leraar die deze positie van

de leerlingen goed begrijpt, is dan ook in de positie de omstandigheden voor de leerlingen doeltreffend te optimaliseren. Dat klinkt manipulatief, maar het is onderwijs hè! Het gaat om het overbrengen van kennis. Leerlingen moeten die kennis consolideren. Dat is de opdracht.