Share this page!

Enter URL or ID to Unroll

You can paste full URL like: https://x.com/threadreaderapp/status/1644127596119195649
or just the ID like: 1644127596119195649

How to get URL link on X (Twitter) App

  1. On the Twitter thread, click on or icon on the bottom
  2. Click again on or Share Via icon
  3. Click on Copy Link to Tweet
  4. Paste it above and click "Unroll Thread"!
  5. More info at Twitter Help
🔥 Matt Dancho (Business Science) 🔥 Profile picture
@mdancho84
May 20, 2023 • 10 tweets • 5 min read • Read on X
Scrolly
BIG ANNOUNCEMENT: I'm beyond excited to announce that in 5 days, I'm launching my brand new course- The #Python for Machine Learning & API's Course.

This course will transform your #career.

Here's what's inside... 🧵

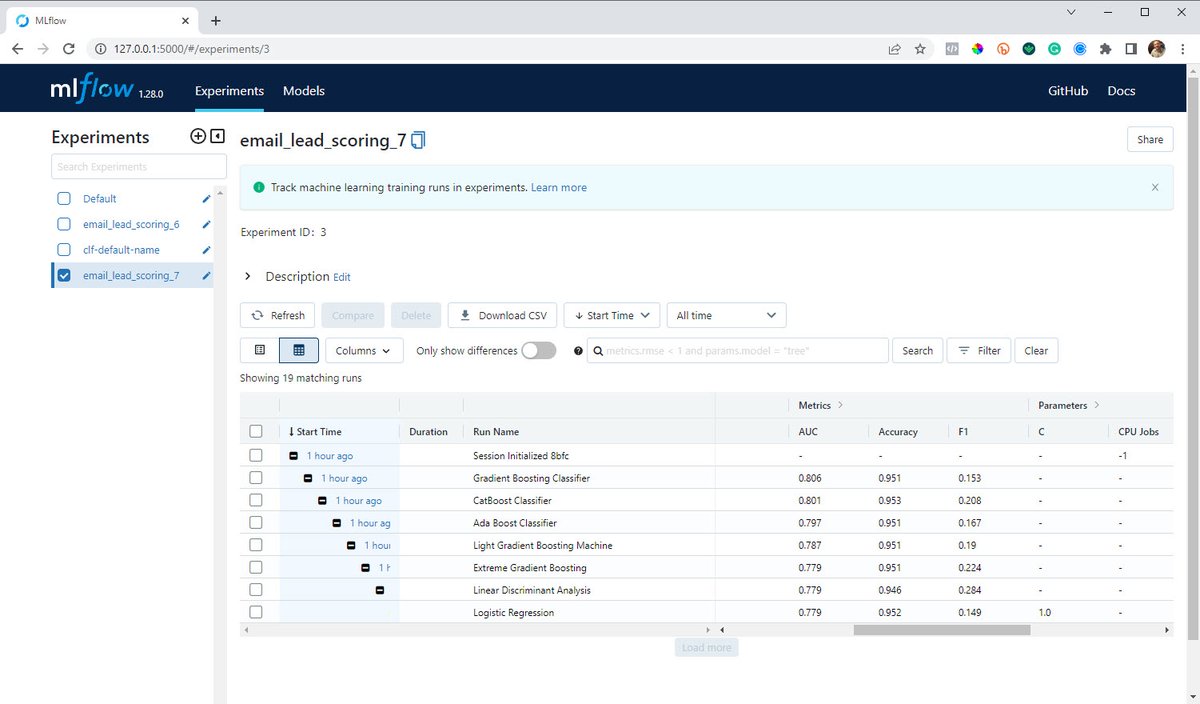
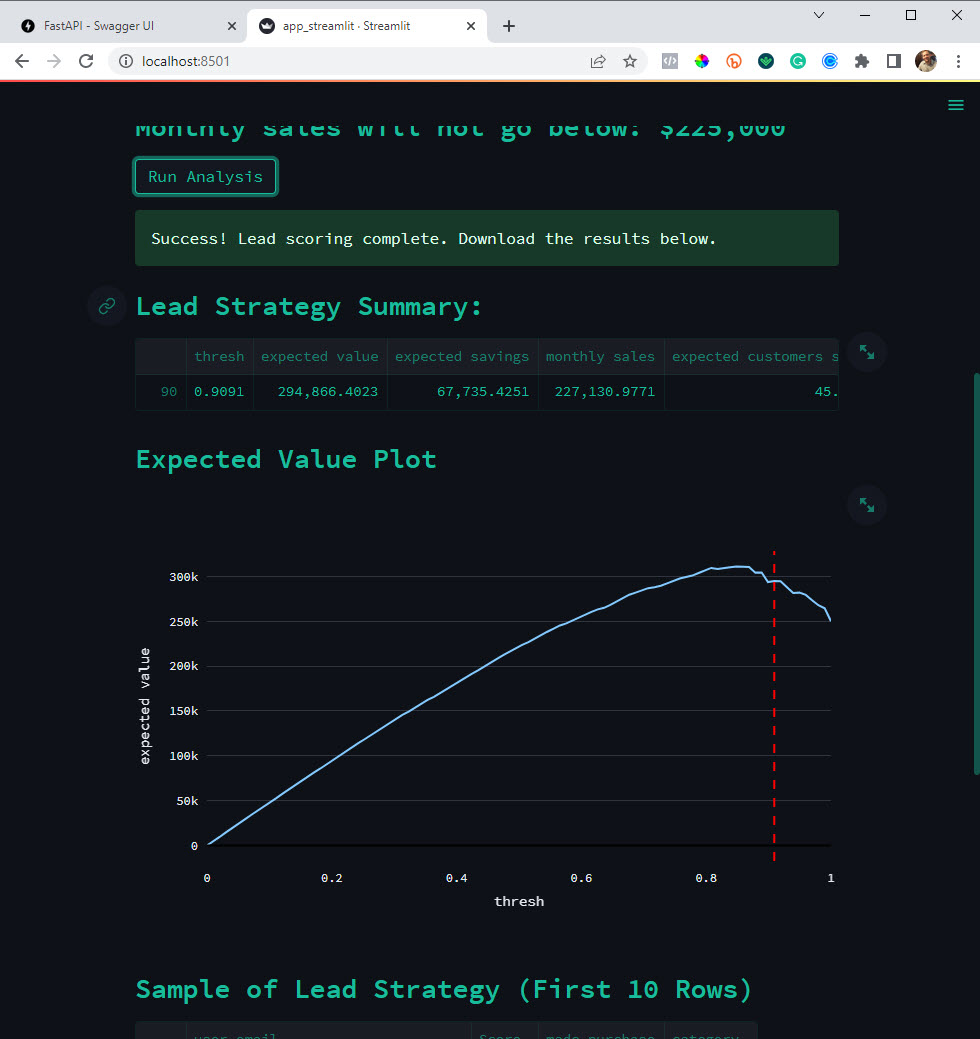
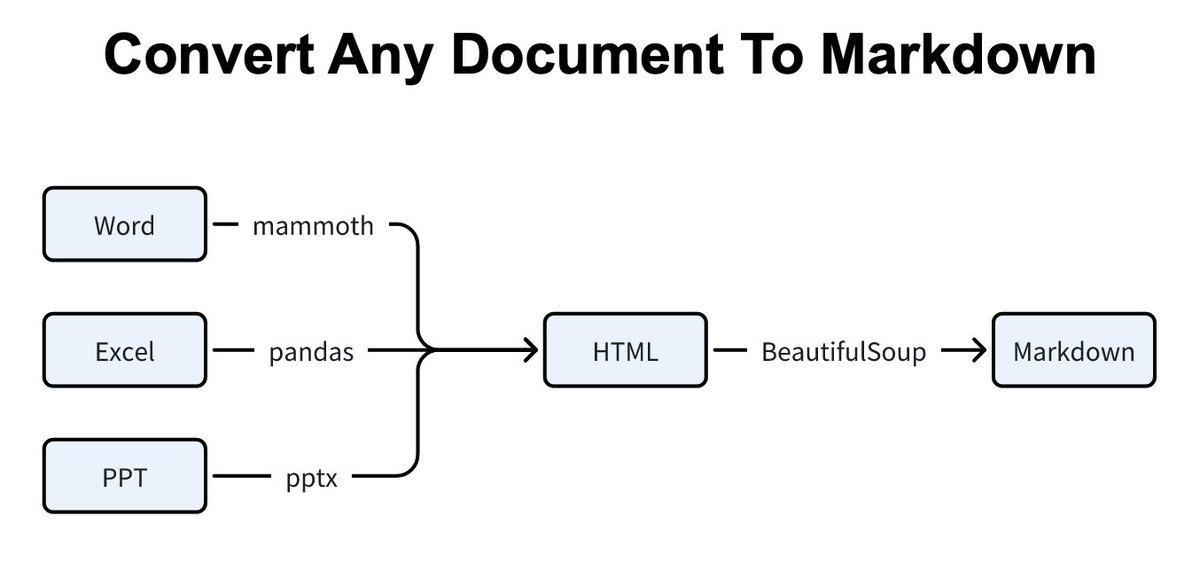
#datascience #course Image
This launch marks the culmination of 2 years of research...

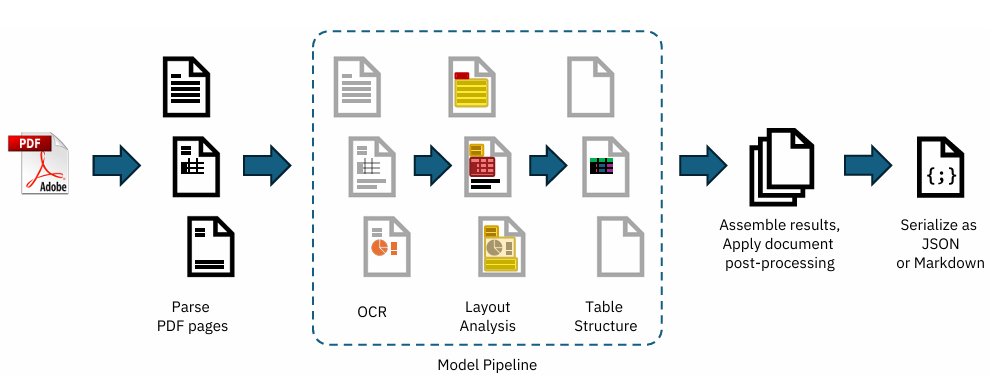
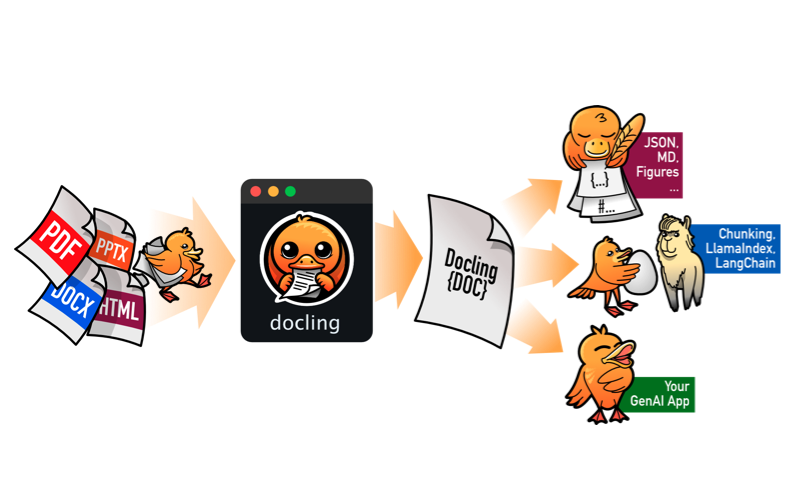
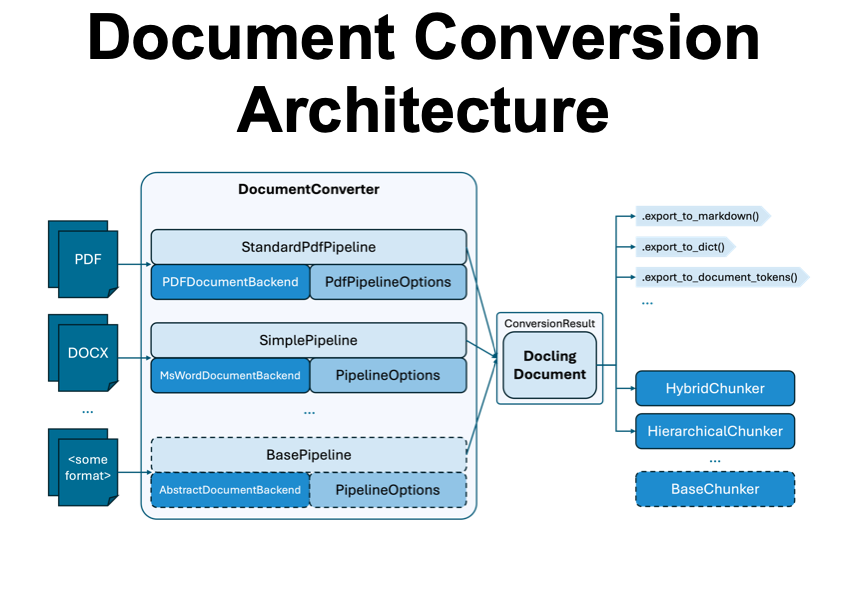
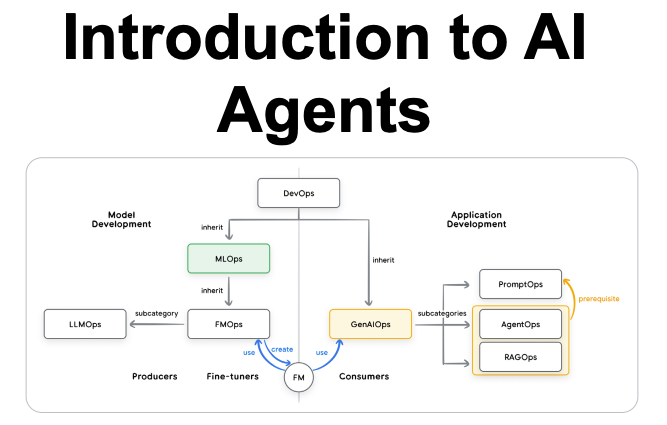
It covers The 6 Top #Python libraries for machine learning and production:
1. #Pycaret: Low-code machine learning Image
2. #ScikitLearn: The premier ML toolkit in Python Image
3. #H2O: Blazing speed + AutoML Image
4. #MLFlow: Easy model lifecycle management Image
5. #FastAPI: Incredibly fast + easy APIs in python Image
6. #Streamlit: Simplified data science web apps Image
Ready to learn more AND advance your career with Python?

Then you can't miss this event.

$400 in giveaways that everyone gets for attending live!
What's the next step?

Just join my course waitlist + live launch event here.

I'm super excited!! 😀

👉Register Here: learn.business-science.io/python-ml-apis… Image

• • •

Missing some Tweet in this thread? You can try to force a refresh
　

Keep Current with 🔥 Matt Dancho (Business Science) 🔥

🔥 Matt Dancho (Business Science) 🔥 Profile picture

Stay in touch and get notified when new unrolls are available from this author!

Read all threads

This Thread may be Removed Anytime!

PDF

Twitter may remove this content at anytime! Save it as PDF for later use!

Try unrolling a thread yourself!

how to unroll video
  1. Follow @ThreadReaderApp to mention us!

  2. From a Twitter thread mention us with a keyword "unroll"
@threadreaderapp unroll

Practice here first or read more on our help page!

More from @mdancho84

🔥 Matt Dancho (Business Science) 🔥 Profile picture
Dec 1
RIP BI Dashboards.

Tools like Tableau and PowerBI are about to become extinct.

This is what's coming (and how to prepare): Image
I've never been a fan of Tableau and PowerBI.

Static dashboards don't answer dynamic business questions.

That's why a new breed of analytics is coming: AI Analytics. Image
AI + Data Science is the future:

AI tools like:

- LangChain
- LangGraph
- OpenAI API

Are being combined with:

- SQL Databases
- Machine Learning
- Prediction

And the results are exactly what businesses need: real-time predictive insights. Image
Read 7 tweets
🔥 Matt Dancho (Business Science) 🔥 Profile picture
Nov 30
Stop Prompting LLMs.
Start Programming LLMs.

Introducing DSPy by Stanford NLP.

This is why you need to learn it: Image
1. Why DSPy?

DSPy is the open-source framework for programming—rather than prompting—language models.

It allows you to iterate fast on building modular AI systems.
2. Modules that express AI programmer-centric way

To build enterprise-grade AI, you need to be able to build modular codebases.

DSPy makes it easy to create these LLM tasks modularly. Image
Read 8 tweets
🔥 Matt Dancho (Business Science) 🔥 Profile picture
Nov 29
This 277-page PDF unlocks the secrets of Large Language Models.

Here's what's inside: 🧵 Image
Chapter 1 introduces the basics of pre-training.

This is the foundation of large language models, and common pre-training methods and model architectures will be discussed here. Image
Chapter 2 introduces generative models, which are the large language models we commonly refer to today.

After presenting the basic process of building these models, you explore how to scale up model training and handle long texts. Image
Read 10 tweets
🔥 Matt Dancho (Business Science) 🔥 Profile picture
Nov 28
🚨BREAKING: New Python library for agentic data processing and ETL with AI

Introducing DocETL.

Here's what you need to know: Image
1. What is DocETL?

It's a tool for creating and executing data processing pipelines, especially suited for complex document processing tasks.

It offers:

- An interactive UI playground
- A Python package for running production pipelines Image
2. DocWrangler

DocWrangler helps you iteratively develop your pipeline:

- Experiment with different prompts and see results in real-time
- Build your pipeline step by step
- Export your finalized pipeline configuration for production use Image
Read 8 tweets
🔥 Matt Dancho (Business Science) 🔥 Profile picture
Nov 27
🚨 BREAKING: Microsoft launches a free Python library that converts ANY document to Markdown

Introducing Markitdown. Let me explain. 🧵 Image
1. Document Parsing Pipelines

MarkItDown is a lightweight Python utility for converting various files to Markdown for use with LLMs and related text analysis pipelines. Image
2. Supported Documents

MarkItDown supports:

- PDF
- PowerPoint
- Word
- Excel
- Images (EXIF metadata and OCR)
- Audio (EXIF metadata and speech transcription)
- HTML
- Text-based formats (CSV, JSON, XML)
- ZIP files (iterates over contents)
- Youtube URLs
- EPubs Image
Read 9 tweets
🔥 Matt Dancho (Business Science) 🔥 Profile picture
Nov 15
The AI Agent Development Process.

How to go from idea to production.

(A thread) 🧵 Image
1. What is the AI Agent Development Process?

A repeatable path to ship an agent from idea to production: define → design → build → train → validate → deploy → monitor → improve.
2. Phases of the Process

Step 1: Defining Purpose

- Identify goals & users
- Determine objectives and success criteria (SLA, budget, accuracy)
Read 11 tweets

Did Thread Reader help you today?

Support us! We are indie developers!

This site is made by just two indie developers on a laptop doing marketing, support and development! Read more about the story.

Become a Premium Member ($3/month or $30/year) and get exclusive features!

Become Premium

Don't want to be a Premium member but still want to support us?

Make a small donation by buying us coffee ($5) or help with server cost ($10)

Donate via Paypal

Or Donate anonymously using crypto!

Ethereum

0xfe58350B80634f60Fa6Dc149a72b4DFbc17D341E copy

Bitcoin

3ATGMxNzCUFzxpMCHL5sWSt4DVtS8UqXpi copy

Thank you for your support!

Follow Us!

Send Email!

:(