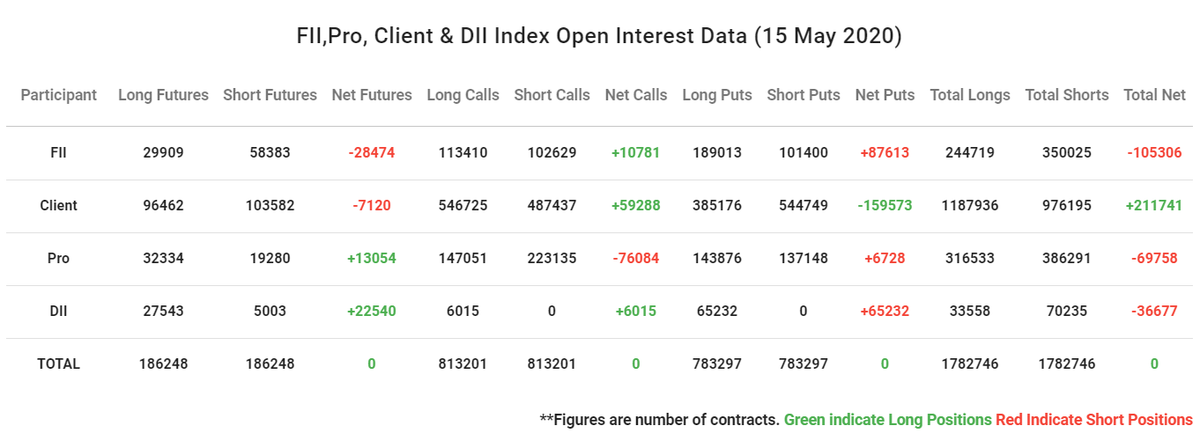
Some new options traders see the options pay-off at expiry & take a trade & then get frustrated to see negative MTM despite being in profit zone as per the pay-off chart.
This thread is to clear such misconceptions and talk about t+0 line and what is its significance
This thread is to clear such misconceptions and talk about t+0 line and what is its significance
In most options software, including opstra, when you place an options strategy, for example, a short straddle, you get a pay-off chart comprising of two parts
The pay-off at Expiry (Green& red chart) and t+0 line (blue dotted line).
See the short straddle example chart here.
The pay-off at Expiry (Green& red chart) and t+0 line (blue dotted line).
See the short straddle example chart here.

The green & red chart showing the profit area and loss area is the absolute pay-off that will happen if the option trade is held till expiry. This is expiry pay-off
The blue-dotted t+0 line is the potential pay-off that is possible as of that day (today). This is t+0 pay-off.
The blue-dotted t+0 line is the potential pay-off that is possible as of that day (today). This is t+0 pay-off.
Expiry pay-off is absolute because the IVs go to zero and all options premiums will be equal to their intrinsic value.
t+0 line pay-off is potential because it is a theoretical & dynamic pay-off calculated using the IVs and days to expiry of individual option legs.
t+0 line pay-off is potential because it is a theoretical & dynamic pay-off calculated using the IVs and days to expiry of individual option legs.
The t+0 line pay-off will keep on changing as the underlying IVs of the options, time to expiry for that day, theta decay, etc keeps changing.
The PNL of an options trade should closely follow the t+0 line pay-off provided the underlying options are liquid.
The PNL of an options trade should closely follow the t+0 line pay-off provided the underlying options are liquid.
The t+0 line pay-off is very important as it tells us immediate risks and opportunities possible with the options trade.
So if you are placing an options trade, the most important thing to see is what t+0 line is telling you.
So if you are placing an options trade, the most important thing to see is what t+0 line is telling you.
The flatter the t+0 line the better it is for the option seller as it gives more room for the strategy to pay-out as theta decay continues.
A curvier t+0 line is better for the option buyer as the strategy will go into profit if the underlying moves in a favorable direction.
A curvier t+0 line is better for the option buyer as the strategy will go into profit if the underlying moves in a favorable direction.
If you observe t+0 line closely, you will see that sometimes the MTM PNL divergence from t+0 line PNL.
This is mainly due to the theoretical nature of the calculation of the t+0 line using Black-Scholes options model which is not a perfect model and has its flaws.
This is mainly due to the theoretical nature of the calculation of the t+0 line using Black-Scholes options model which is not a perfect model and has its flaws.
And finally, its called t+0 (time plus zero) line because its the pay-off at time zero, that is, current day.
• • •
Missing some Tweet in this thread? You can try to
force a refresh