Thread by @Arnaldo_AGITF

After some time in Twitter hibernation, I'm back with a microlesson on a topic I didn't have space to talk about in my book—sound!

Let's talk about what sound is, how it happens, and figure out how fast it is! #fluids #sound #physics

First things first. How does sound happen?

The first ingredient is matter. Air, water, even solids can transmit sound; but you can't have sound without one of these mediums. That's why you can't make sound in space—there's barely anything there!

An important thing to remember about matter is that isn't just a "blob" of stuff—it's actually a massive pile of tiny atoms/molecules bouncing around & off of each other in a complex, highly unpredictable dance.

As a result, when you push on matter, the particles that make up that matter get pushed, which causes those particles to push on their neighbors, which causes THEM to push their neighbors, and so forth.

That process is what we call sound!

We can hear sound because that "push" eventually reaches the walls of our eardrums, which causes them to vibrate in a way that our brains can interpret pretty well. Pretty convenient, huh?

One reason sound is used by animals to communicate is because of how fast it is—the "push" travels at 343 meters per second (or 768 mph) in air. I can't imagine we'd talk much if it moved at 0.1 mph.

But why is it so fast, and what determines how fast it is? Let's do some math!

We fluid mechanicians use a property called density—which is a ratio of the mass of matter inside some container to the container's volume—to describe sound.

In that sense, sound changes density in the vicinity of the "push". So how does that change in density lead to motion?

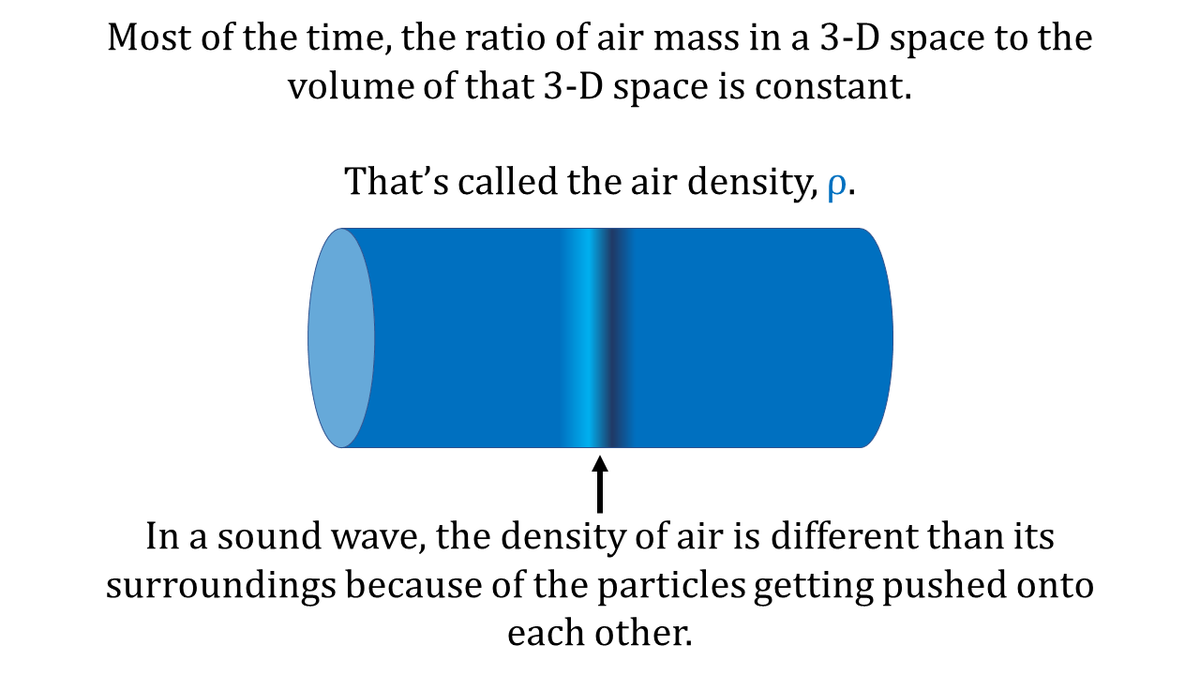
Let's consider a tube filled with originally still air and a sound-making device, which pushes the air in a way that changes the density of the air and causes motion plus a change in air pressure.

Let's investigate how each of these things depends on each other in a sound wave!

We know that we're not destroying or creating matter in this pipe, so mass needs to be conserved. For this scenario, this is what conservation of mass looks like mathematically.

(If you're not super familiar with fluid mechanics, don't worry—just trust me!)

Similarly, momentum is also conserved, so any change in the kinetic energy of the air needs to come from the speaker "pushing" on the air.

Shockingly, these two conservation principles are all we need to find an expression for the speed of sound!

Doing some calculus and algebra based on those previous conservation equations, we find something pretty neat:

The speed of the sound wave has to be the square root of the change in the air pressure when the density of the air gets altered by the sound-maker!

This lets me measure what the speed of sound is in air without making any sound!

All I have to do is take a container of air, push down on it, and find the ratio of the pressure I'm applying vs. the change in the air's density. The square root of that is air's speed of sound!

That's not too shocking—if molecules in matter don't like being pushed against neighbors, they'll quickly push & go back to where they were, making the sound wave move faster.

That's it for this microlesson! Based on this, do you think sound is faster in air or water? Chime in!

P.S.: If you'd like to learn about where those expressions for conservation of mass/momentum came from, or just want to learn more about fluid mechanics in general, take a look at my free book on fluid mechanics below!

google.com/books/edition/…