Share this page!

黒木玄 Gen Kuroki Profile picture
Twitter logo
9 Oct, 39 tweets, 20 min read
#Julia言語 リンク先のリンク先のブログ記事に言及している人が多い！私が書いたんじゃないけど、なんかうれしい。

細かいケアレスミスがあってもそういうのは本質ではなくて、おもろいネタで長文を書きまくっていて楽しそうな点が秀逸！

JuliaとLispのマクロの話がウケるというのもすごい話！
#Julia言語 #Lisp 何はともあれ拡散
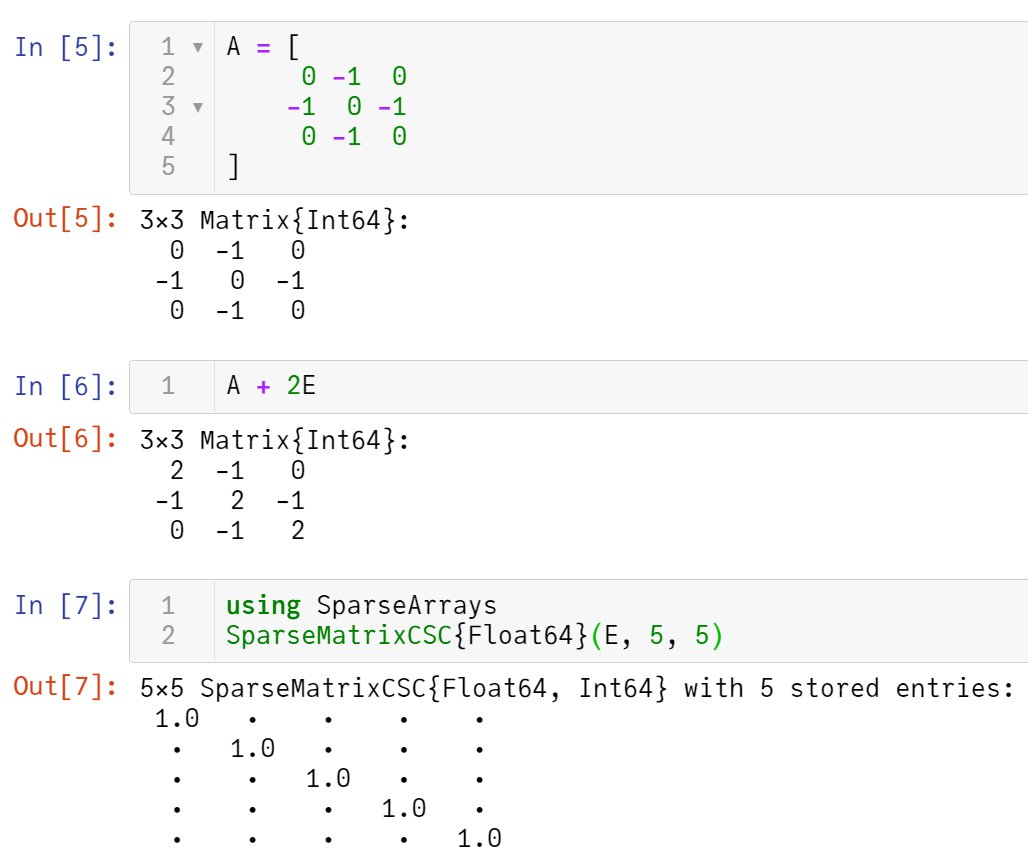
#Julia言語 Juliaのマクロを理解するために役に立つ情報(ネタ)

S式風のタプル式

(:call, :sin, (:call, ;/, π, 6))

をJuliaの式

Expr(:call, :sin, Expr(:call, ;/, π, 6))

に変換して実行するマクロ。これは :(sin(π/6)) に等しい。

この辺の知識があるとJuliaのマクロを理解し易くなる。
#Julia言語 関連スレッド
#Lisp これも見逃せない。
#Julia言語 いつもお世話になっていてかつ速くてびっくりのあんちもん2さん。head :vect を head :tuple に置き換える「手抜き」の話。

Juliaだとネストしたタプルを左辺で使える。例えば

(a, (b, c)) = (1, (2, 3))

でa,b,cをそれぞれ1,2,3にできる。
#Julia言語

gist.github.com/genkuroki/b410…
tuple processing language.ipynb

Lisp-like example を追加した。

タプルで書かれたLispっぽいコードがJuliaの式に変換されて実行されています。

これを見れば、Lispを知っている人はJuliaについて理解し易いかも。car, cdrの定義は上のリンク先を参照。
＃Julia言語 タプルで書かれたLispっぽいコードはたった数行のプログラムでJuliaで実行可能な式に変換できます(添付画像1のtuple2expr函数)。

こういうことができる点も、Juliaが教育用プログラミング言語として__も__使えると私が考えるゆえん。

gist.github.com/genkuroki/b410…
#Julia言語 相互リンク

#Julia言語 再掲

* JuliaでのExprの直接操作によるマクロとLispでののマクロの優劣はないと私は思う。

* Juliaにおいて「人間に易しい表示」でもマクロを易しく書けるとありがたいが、現時点では無理だと私は思う。今後の発展に期待したい。
#Julia言語 JuliaにおけるExprの理解のためには

gist.github.com/genkuroki/fe9c…

を参照。添付画像では同一のExpr

:(function bar(a::T; b = 456) where T <: Real
println(a, " + ", b, " = ", a + b)
a + b
end)

の表現集です。見かけが違うだけで全部同じという認識が大事。
#Julia言語 JuliaのExprの直接的構成によって、タプルで書かれたLisp風のコードを容易に実行可能にできることについては

gist.github.com/genkuroki/b410…

を参照。添付画像のようなことをできる。

もちろんこれは【ネタ】で、ゲラゲラ笑ってもらえるとうれしいです。😊
#Julia言語 #マクロ 【ネタ】

using Plots
plot(sin; label="sin(x)", size=(400, 250))

と同じことを添付画像のように「タプル式」の実行でも可能(笑)。

gist.github.com/genkuroki/b410…
#Julia言語 参考情報

Common LispからJuliaに引っ越した人がその理由を次のリンク先で述べています。

tamaspapp.eu/post/common-li…

JuliaにはCommon LispやDylanに似ている。同じ人による「Common LispとDylanとJuliaの優位性」に関するコメント↓

discourse.julialang.org/t/design-patte…

関連
#Julia言語

julia-users.narkive.com/bs3abQsV/julia…
【Stefan Karpinski

We were never directly influenced by Dylan.～Any linguistic
similarities are due to common influences (e.g. Lisp, Pascal, Algol),～I'm not sure what the reasons were for
Dylan choosing multiple dispatch, but for us ～】
#Julia言語 既出の

julia-users.narkive.com/bs3abQsV/julia…

tamaspapp.eu/post/common-li…

の両方で強調されていることは、数値計算における

* 成分の型が前もって決まっていない配列への対応の必要性。

成分の型が異なる配列の計算でコードを共有したい。しかも前もって予定していなかった成分の型も許したい。続く
#Julia言語 Float64やFloat32の通常の配列、GPUで計算される配列、それらの複素数版やdual number版(自動微分)、成分が配列の配列、などなどについて、可能な限りコードを共有し、それぞれに関わる部分のコードの特殊化は必要最小限で済ませたい。

Juliaは最初からそうできるように設計されていた。
#Julia言語

JuliaのマクロもJuliaのすべての機能を使えます。
何でもあり。

しかし、私はそれが普通だと思っていた。

Juliaのそういう所はCommon Lispに似ている。

Common LispからJuliaへの移住者の例↓
tamaspapp.eu/post/common-li…
#Julia言語 マクロ

macro foo(x, y, z)
～
end

は

@ foo A B C

の形式で使用できます(@ の直後の空白は削除)。A, B, Cは1つの式になるJuliaのコードです。このとき、マクロfooは引数x,y,zとしてA,B,Cをパースした結果を受け取ります。パースした結果もJuliaで普通に操作可能。続く
#Julia言語 続き。マクロは引数としてコードをパースした結果である「式」を受け取り、実行可能な「式」を返す任意の函数として定義されます。マクロを実行すると、マクロの返り値の「式」が自動的に実行される。

マクロはそのような任意の函数として定義されるのでJuliaのすべての機能を使えます。
#Julia言語 1つ前のツイートの「式」は、具体的な値(数値、文字列、配列、辞書、シンボル、…)またはそれらを組み合わせたExpr型オブジェクトになり、Juliaのすべての機能を使って操作可能です。その意味の「式」のイメージは、「式」で遊んでみればすぐに得られます。

そのために書いたのが～続く
#Julia言語 続き～

gist.github.com/genkuroki/b410…
tuple processing language

です。空行とコメントを除くと13行しかない。

@ teval はタプルで書かれたLisp風の式をJuliaで実行可能な「式」に変換して実行するまくろです。

タプルで書かれた式で、Plotsパッケージを読み込んでグラフも書ける。
#Julia言語 Lisp風のタプルで書かれた式を得るには、例えば、

Meta. show_sexpr(:(sin(π/6))

を実行します。結果は

(:call, :sin, (:call, ./, π, 6))

になります。これを @ tevalで実行すると

0.49999999999999994

がえられる。@ tevalでは、:call をある程度省略可能にしてあります。
#Julia言語

(:call, :sin, (:call, :/, π, 6))

はJuliaで実行可能な「式」の

Expr(:call, :sin, Expr(:call, :/, π, 6))

に変換されます。見た目的には単にExprを追加しただけ。

以上を知っていると、Juliaのマクロで扱っている「式」がどういうものかについて、具体的なイメージを持てます。
以上で一ヶ所 ./ となっているのはもちろん :/ の誤植です。
#Julia言語 では、Juliaのコードをパースした結果を表す

:(sin(π/6))

は

Expr(:call, :sin, Expr(:call, :/, π, 6))

に等しいです。これをMeta. show_sexpr函数は

(:call, :sin, (:call, :/, π, 6))

と表示し、私の@ tevalマクロはこれを :(sin(π/6)) に変換して実行してくれます。
#Julia言語 以上の遊び を繰り返せば、Expr型オブジェクトのイメージがつかめます。しかし、その中身の操作もできるようになるためには、内部構造をdumpして確認する経験も必要です。

dump(:(sin(π/6)))

または

Meta. @ dump sin(π/6)

で中身の詳細が見える。

gist.github.com/genkuroki/b410…
#Julia言語 Juliaが文字列をどのようにパースするかは、

Meta. parse("sin(π/6)")

などで分かります。しかし、これは

:(sin(π/6))

になるので、こちらの方が必要な入力文字数は小さい。
#Julia言語 野良パッケージ

InteractiveUtilsPlus.jlの名前をMetaUtils.jlに変えて、リスプっぽいタプルで書かれた式を評価してくれるマクロ @ teval を追加しました。その過程で色々バグを取った。

github.com/genkuroki/Meta…
#Julia言語 既出のJupyter notebookの「名前空間由来のバグ」をとったバージョン↓

gist.github.com/genkuroki/b410…
#Julia言語 #Lisp 反響

マクロの話は私ももっとよく理解したい。
#Julia言語 #Lisp 以下のリンク先のスレッドの特に以下にリンクした解説は非常に助かった。ありがとうございました！
#Julia言語 #Lisp しかし、

muuuminsan.hatenablog.com/entry/2020/10/…
コメント欄【Lispでなければ簡単に表現/作成/運用できないマクロというのはある】

はわたしには理解不可能。以下を具体的なコード例で示さないと証拠にならない。

①Lispでは簡単なマクロ
②そのJulia版を作る試みの結果
③Juliaで失敗する理由
#Julia言語 #Lisp

同コメントより【データ->AST->コードでは、データとコードの見た目と操作方法に乖離があるので、Lispほど直截的で簡単なデバッグはできません。】

条件を揃えるためには「S式を楽に解釈できること」と「JuliaのExpr式を楽に解釈できること」の両方を前提にする必要があり～続く
#Julia言語 #Lisp 続き～、比較の仕方としてはフェアではないと思いました。

* 常にS式を扱うことを強制されるデメリット

と

* 普段はsin(π/6)という書き方をできるが、マクロを書くときにのみ(:call, :sin, (:call, :/, π, 6))という構造の取扱いを強制されることのデメリット

の比較の問題。
#Julia言語 Juliaのマクロを自分で書くことについては、現時点ではユーザーフレンドリーとはとても言えない状況。

TeXで言えば、LaTeXさえ存在していなくて、式番号を手動で付けていた時代に似ていると思う。

原理的に「何でもできる」世界なので、楽に使える方向に何か発展があってもよいと思う。
#Julia言語 すでに完成品になっていて、よく使われているJuliaのマクロをユーザー側が利用するのはやさしいです(TeXの場合と同じ)。

使用例はJulia本体やパッケージのリポジトリにあるソースコードをみれば幾らでもサンプルコードが得られる。Googleによる検索よりも圧倒的に効率が良いです。
関連スレッド

• • •

Missing some Tweet in this thread? You can try to force a refresh
　

Keep Current with 黒木玄 Gen Kuroki

黒木玄 Gen Kuroki Profile picture

Stay in touch and get notified when new unrolls are available from this author!

Read all threads

This Thread may be Removed Anytime!

PDF

Twitter may remove this content at anytime! Save it as PDF for later use!

Try unrolling a thread yourself!

how to unroll video
  1. Follow @ThreadReaderApp to mention us!

  2. From a Twitter thread mention us with a keyword "unroll"
@threadreaderapp unroll

Practice here first or read more on our help page!

More from @genkuroki

黒木玄 Gen Kuroki Profile picture
11 Oct
#Julia言語 や #Lisp のマクロは難しいです。

そういう難しいものについては、

* プログラミングの専門家以外は使えなくてもよい

という考え方もありだと思う。しかし、

* 必ずしもそうとは言えない場合もある

と私は考えています。例えば、特殊函数の専門家の数学者が～続く
#Julia言語 例えば、特殊函数論が専門の数学者が自分が愛している有用な特殊函数の数値計算ライブラリを作って配布したいと思ったとします。

特殊函数の数値計算は多項式や有理函数による近似に帰着する場合が多く、「係数をべた書きしたホーナー法」で書くと計算が効率的になります。続く
#Julia言語 続き。しかし、そのようなコードを数学者に直接書かせることは効率的ではありません。

数学者が知っている係数の計算法に従って係数が自動的に計算され、それが「係数をべた書きしたホーナー法」のコードに自動変換される仕組みが好ましいです。

まさにそれをやるのがマクロです！
Read 12 tweets
黒木玄 Gen Kuroki Profile picture
9 Oct
#Julia言語 【ネタ】tuple processing language

S式っぽいタプルでJuliaの式を与えると、それを解釈して実行してくれるマクロ(笑)

空行とコメントを合わせても33行しかありません。続く

gist.github.com/genkuroki/b410… Image
#Julia言語 タプル式でsin(π/6)を計算してみましょう。

(:call, :sin, (:call, :/, π, 6))

を実行すれば sin(π/6) を計算できます。:call を省略して

(:sin, (:/, π, 6))

でも同じ結果が得られるようにしてあります。続く Image
#Julia言語 タプル式で函数も定義できます。

(:(=), (:call, :f, :x), (:call, :sin, :x))

で f(x) = sin(x) と定義できます。In[4]ではそのようにして定義した f(x) を使って f(π/6) を計算しています。続く Image
Read 8 tweets
黒木玄 Gen Kuroki Profile picture
9 Oct
#Julia言語 「最初のプロットの遅延問題」は有名な欠点で、nightly buildで大きな改善されています。

遅いのは「最初のプロット」だけなので、プロット用のコードを書いたfoo.jlについて毎回

julia foo.jl

としていなければ大した問題にはならないです。

juliaは再起動の回数を減らして使いたい。
#Julia言語 REPL、Jupyter、Juno、VSCode内でJuliaを使い、コードを書き始める前に、

using Plots
plot(sin)

を実行しておいて、その後にプロット用のコードを書いて実行すれば実質的に待ち時間はゼロ。
#Julia言語 公式ドキュメントの

docs.julialang.org/en/v1/manual/w…

の方法：Jupyter

github.com/JuliaLang/IJul…

を使ったり、Revise.jl

github.com/timholy/Revise…

を使って、

julia> using Revise
julia> includet("foo.jl")
julia> plot_foo()
失敗→foo.jlを編集→編集結果が自動反映
julia> plot_foo()
Read 4 tweets
黒木玄 Gen Kuroki Profile picture
9 Oct
#Julia言語 nightly build で、パッケージA.jlの中のXをYという名前で使いたい場合に

using A: X as Y

とできるようになっていますね。

github.com/JuliaLang/juli…

添付画像はすでにIを使ってしまっているので、

using LinearAlgebra: I as E

としている場合。

gist.github.com/genkuroki/d812…
#Julia言語 個人的には

import LinearAlgebra as linalg

として

A = randn(100, 100)
fac = linalg. lu(A)
e = linalg. eigen(A)

のように、「わざわざ」もしくは「必然性不明の短縮」で至る所 linalg. を付けて書くようなスタイルを使う人が

増えないで欲しいな

と思います。
#Julia言語 Pythonという特殊で一般性に欠けた世界の1つで普通になっている方法で import as を使う人が増えるのは、私も不快。

このスレのトップで紹介したように「すでにIを使っているので、LinearAlgebra.jlのIをEという名で使うため」に、

using LinearAlgebra: I as E

とできるのは便利。
Read 5 tweets
黒木玄 Gen Kuroki Profile picture
9 Oct
#統計

標本のばらつきの指標として
分散を採用する必然性は__ない__。
中央値との差の絶対値の加法平均も
立派なばらつきの指標である

という話は繰り返ししている。
しかも、Laplace分布モデルとの関係まで言及している。

繰り返し言及していることの証拠↓
twilog.org/genkuroki/sear…
#統計

標本平均と標本分散の計算
=正規分布モデルによる最尤推定

標本の中央値との中央値との差の絶対値の平均の計算
=Laplace分布モデルによる最尤推定

こういう関係。

「標本の代表値としてどれを重用するか」と
「どのような統計モデルで推定するか」の間には
上のような関係がある。
#統計 モデルが現実に合ってなければ捨てられるのはモデルの側なのに、実質正規分布モデルによる推定になっている「代表値としての分散の採用」にまるで必然性があるかのような説明をしようとしている場合が結構あるように見える。

大学の先生でもこの点はかなりひどいのでは？
Read 14 tweets
黒木玄 Gen Kuroki Profile picture
9 Oct
Re: RT #数楽

Bernoulli多項式を「特殊値」として持つゼータ函数はHurwitzのゼータ函数である。(その特別な場合がRiemannのゼータ函数)

問題：それと同様の意味でHermiteの多項式を「特殊値」として持つゼータ函数に類似はあるか？

答え：ある‼️↓
nbviewer.jupyter.org/github/genkuro…
#数楽 区間[0,1]上の一様分布の分配函数(=モーメント母函数)の

Z(β) = ∫_0^1 e^{-βx} dx = (e^{-β} - 1)/(-β)

の逆数とベルヌイ数の母函数は本質的に一致し、統計力学の意味での[0,1]上のカノニカル分布

e^{-βx}/Z(β) = (-β)e^{-βx}/(e^{-β} - 1)

はベルヌイ多項式の母函数に本質的に一致する。
#数楽 Hurwitzのゼータ函数は[0,1]上の一様分布のカノニカル分布のMellin変換に本質的に一致する。

これを、ℝ上の(適当な条件を満たす)任意の確率分布のカノニカル分布のMellin変換に一般化すれば、一般化されたHurwitzのゼータ函数が定義される。
Read 6 tweets

Did Thread Reader help you today?

Support us! We are indie developers!

This site is made by just two indie developers on a laptop doing marketing, support and development! Read more about the story.

Become a Premium Member ($3/month or $30/year) and get exclusive features!

Become Premium

Too expensive? Make a small donation by buying us coffee ($5) or help with server cost ($10)

Donate via Paypal Become our Patreon

Thank you for your support!

Follow Us on Twitter!

Like this author's thread?

Get email notifications when new thread is out from this Author!

Check out other threads from this Author!

Read all threads by @genkuroki