Thread by @svpino

Bias vs. variance in 13 charts.

🧵👇

Here is a sample 2-dimensional dataset.

(We are just representing here the training data.)

👇

The red line represents a model.

Let's call it "Model A."

A very simple model. Just a straight line.

👇

Here we have a much more complex model.

Let's call this one "Model B."

👇

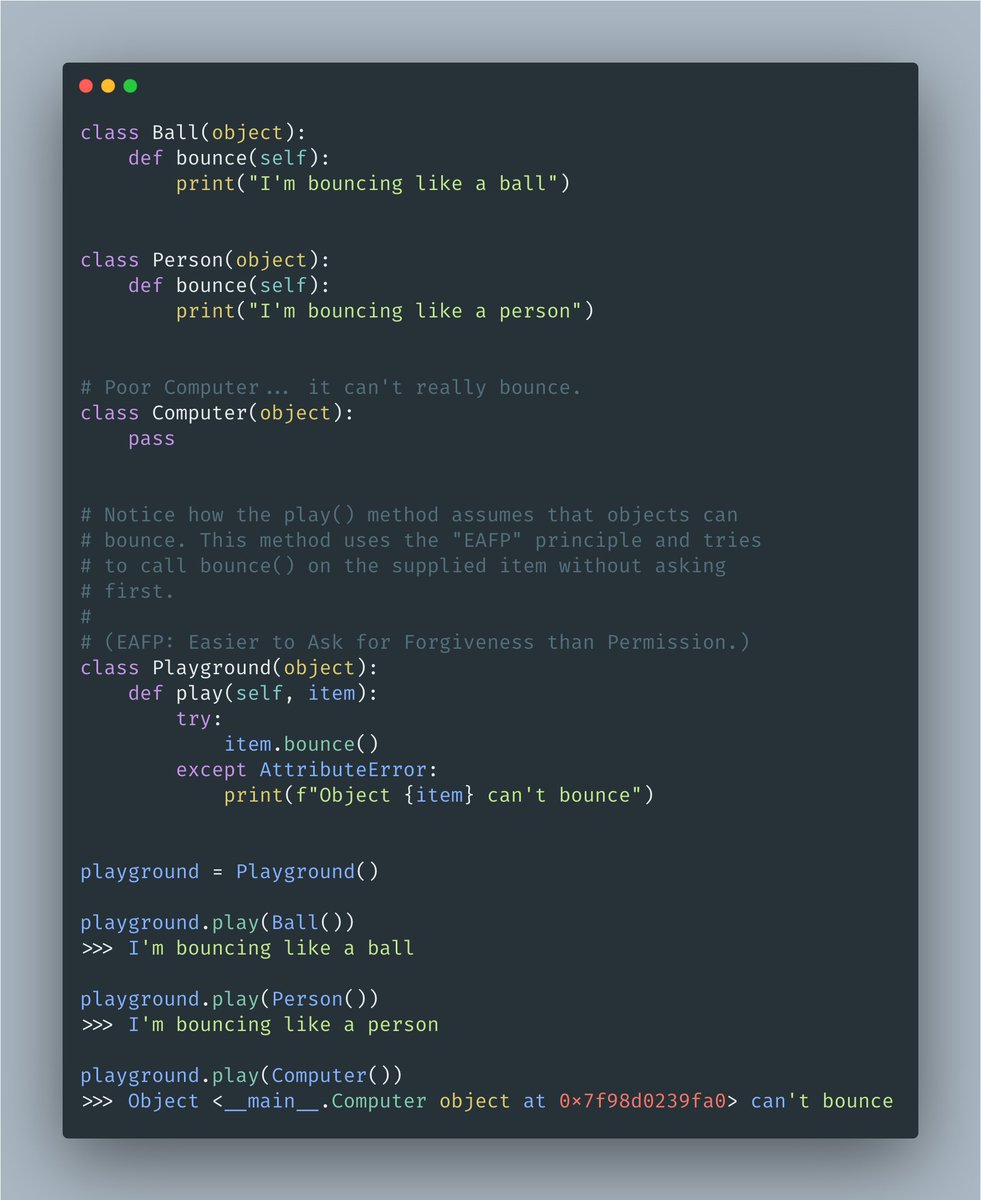
Let's compute Model A's error.

We can add up all the yellow distances together to come up with this error (we usually sum up the square of the distances to avoid positives values to cancel with negative values.)

The error is high.

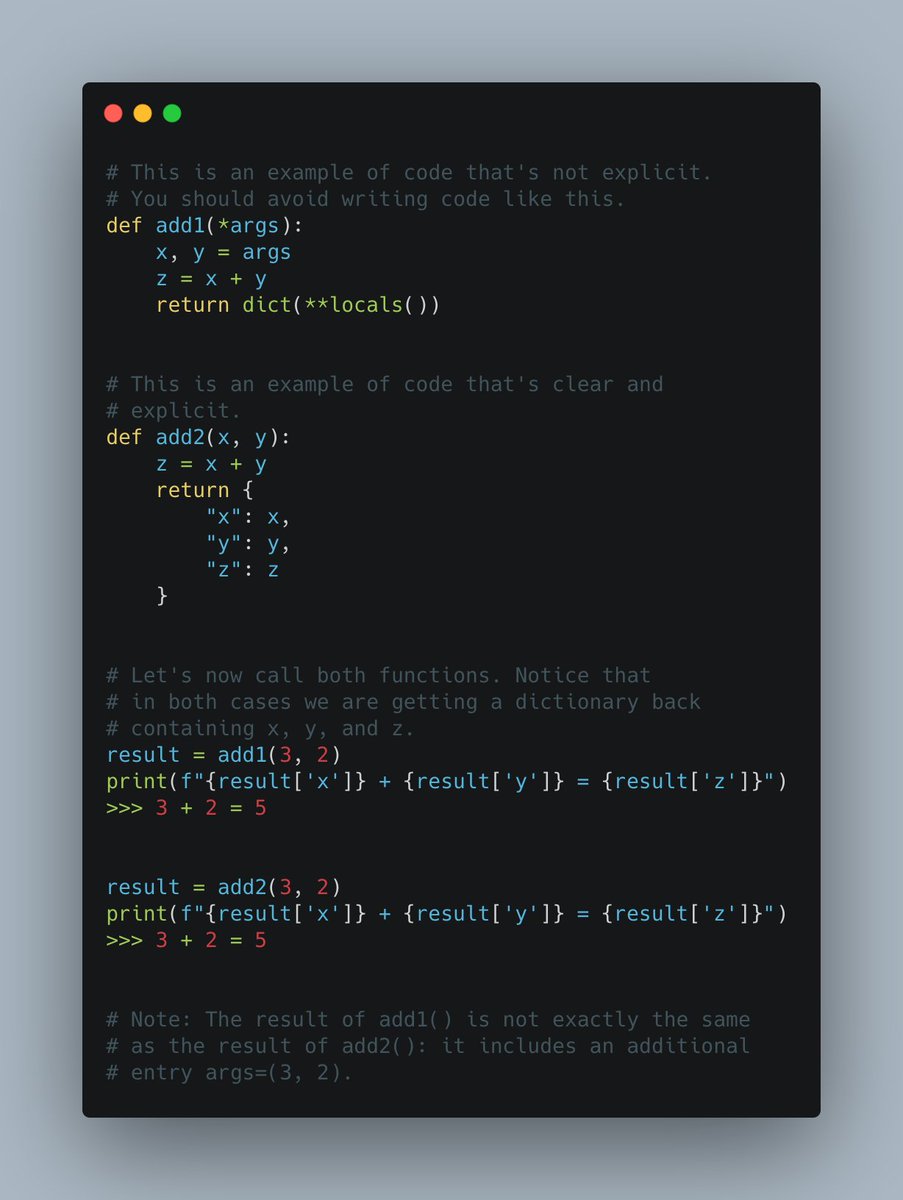
Let's now compute Model B's error.

Well, this error it's pretty much zero!

Model B is very complex and fits the training data perfectly.

Apparently, Model B is much better than Model A, right?

Well, not necessarily. Let's introduce a validation dataset (blue dots) and compute the error of each model again.

Here is Model A's error. The model performs consistently bad on the validation data.

👇

When computing Model B's error, we realize that it is not zero anymore.

The model performs much worse on the validation data than on the training data.

This is not a consistent model. This is not good.

Neither Model A nor B is good.

👇

We say that Model A shows *high bias* and *low variance*.

A straight line doesn't have enough expressiveness to fit the data.

We say that this model *underfits* the data.

👇

We say that Model B shows *high variance* and *low bias*.

The model has too much expressiveness and "memorizes" the training data (instead of generalizing.)

We say that this model *overfits* the data.

👇

What we want is Model C.

A model that properly balances bias and variance in a way that's able to generalize and give good predictions for unseen data.

Remember this: The bias vs. variance tradeoff is a constant battle you have to fight.

👇

Finally, let's look at how the bias and variance tradeoff play out as we increase our models' complexity.

Let's represent the error of the model on the training set as we vary its complexity.

👇

Let's now do the same with the error on the validation data (a dataset that the model didn't see while training.)

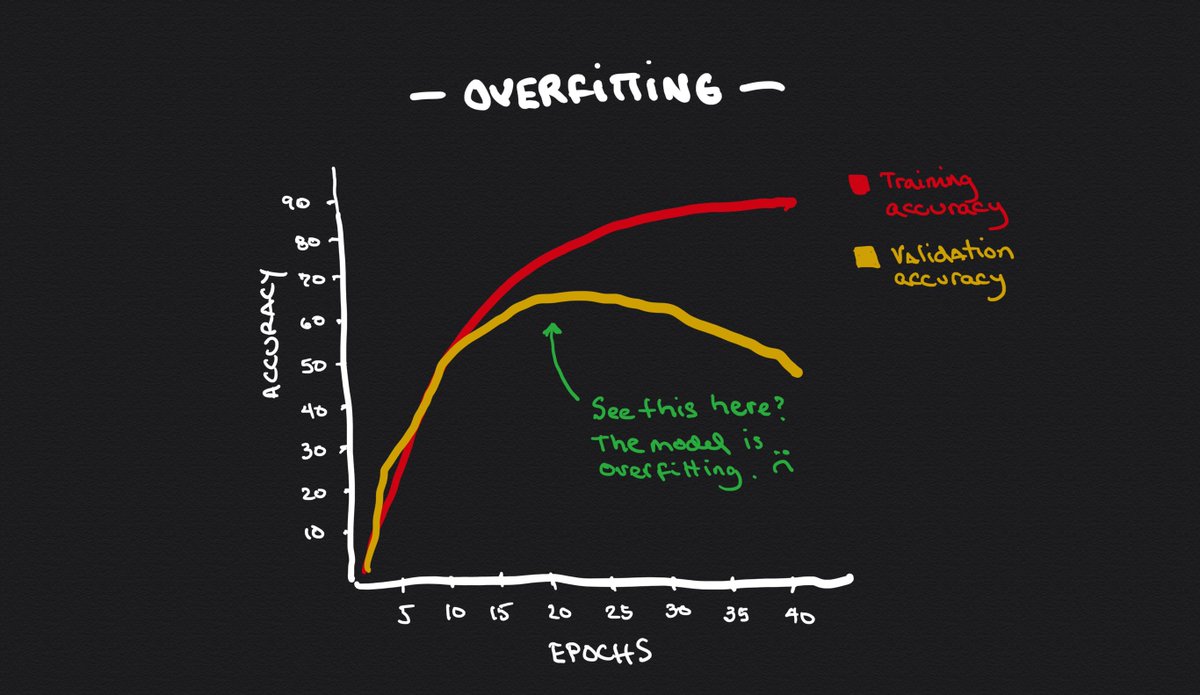
See what happened here?

The more complex the model becomes, the worse it does on the validation set.

👇

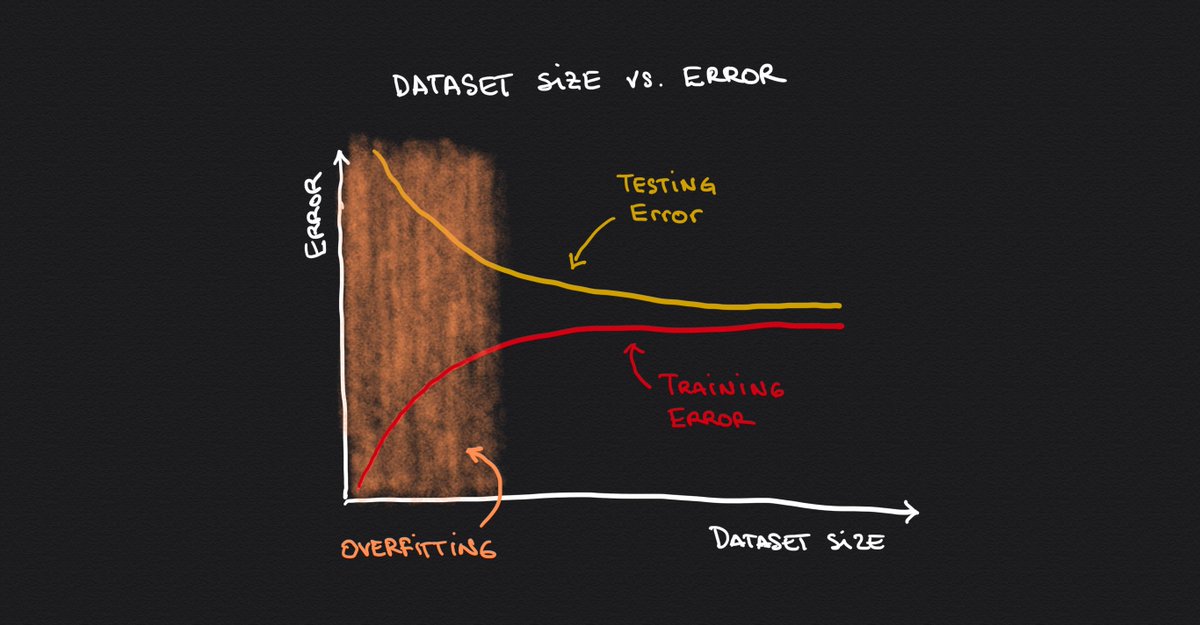
Breaking it down into three sections:

▫️Green: We are underfitting.
▫️Yellow: We are overfitting.
▫️Orange: Just right.

We want to be in the middle section. That's the right balance of bias vs. variance.

A thread about preventing overfitting:

https://twitter.com/svpino/status/1318279226668257282?s=20