Thread by @andrewgwils

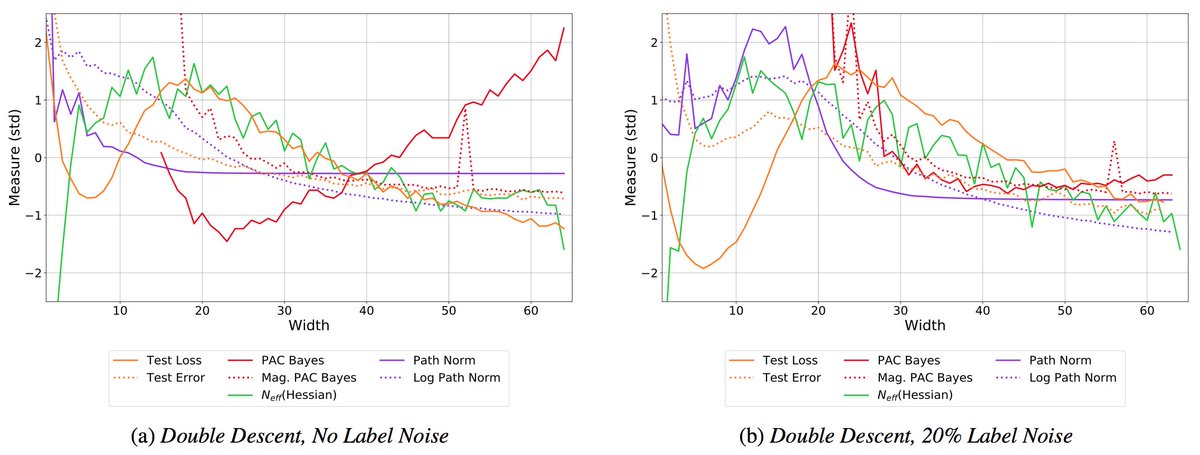
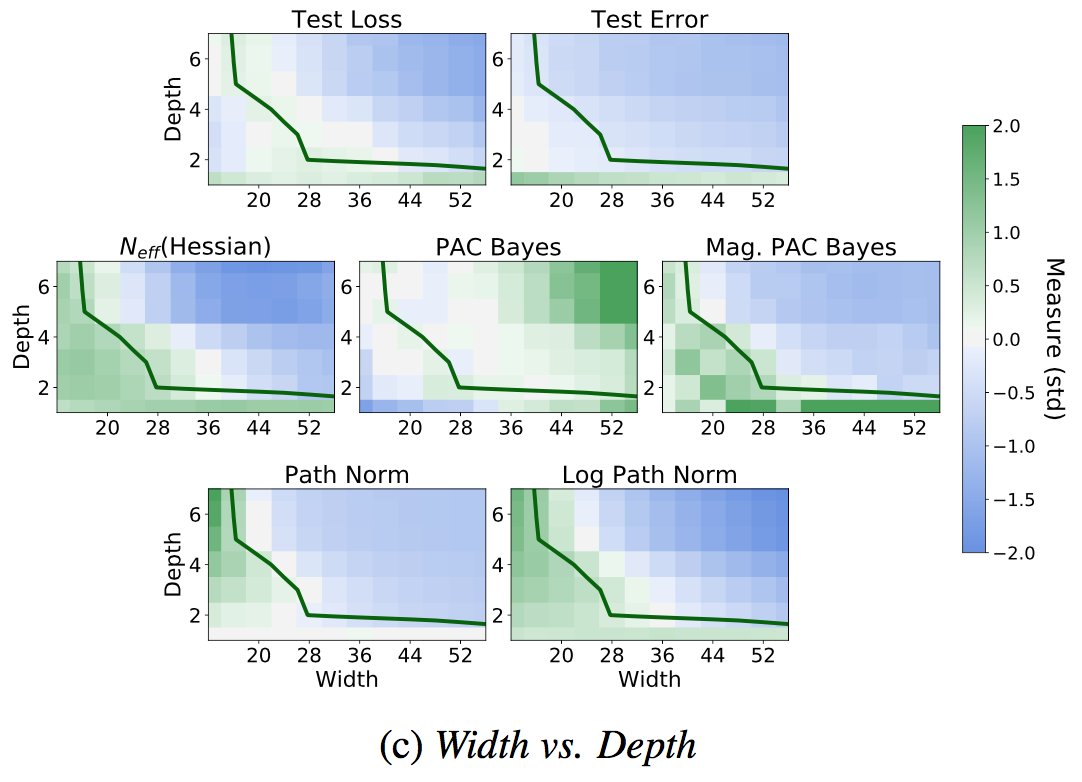
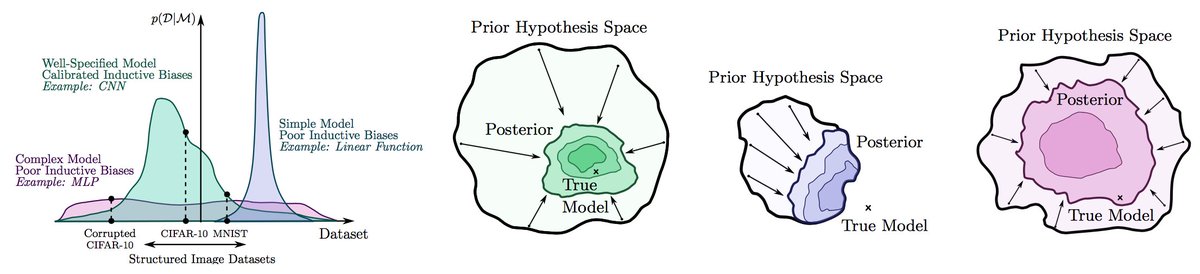
We can greatly simplify Hamiltonian and Lagrangian neural nets by working in Cartesian coordinates with explicit constraints, leading to dramatic performance improvements! Our #NeurIPS2020 paper: arxiv.org/abs/2010.13581
with @m_finzi, @KAlexanderWang. 1/5

Complex dynamics can be described more simply with higher levels of abstraction. For example, a trajectory can be found by solving a differential equation. The differential equation can in turn be derived by a simpler Hamiltonian or Lagrangian, which is easier to model. 2/5

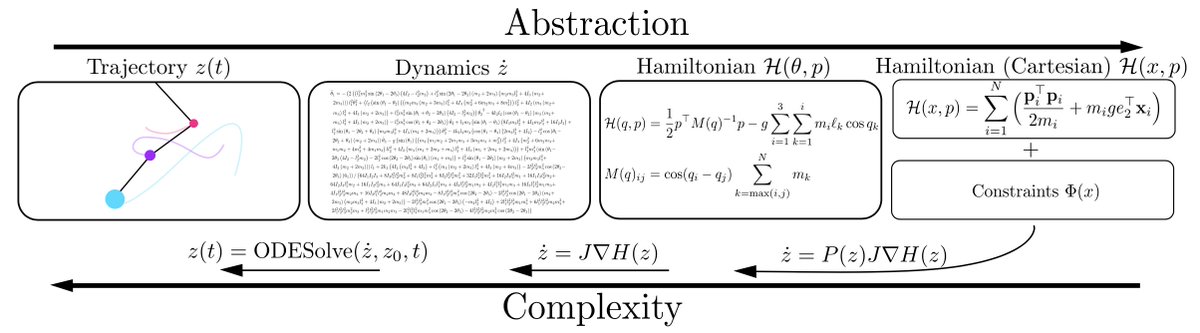
We can move further up the hierarchy of abstraction by working in Cartesian coordinates and explicitly representing constraints with Lagrange multipliers, for constrained Hamiltonian and Lagrangian neural networks (CHNNs and CLNNs) that face a much easier learning problem. 3/5

We show how to apply our approach to arbitrary rigid body and extended systems by showing how such systems can be embedded into Cartesian coordinates. We also introduce a series of chaotic and 3D extended body systems that challenge current approaches. 4/5

Much more in the paper! Code is also available at: github.com/mfinzi/constra…
5/5