Share this page!

Adam Kucharski Profile picture
Twitter logo
29 Dec, 4 tweets, 2 min read
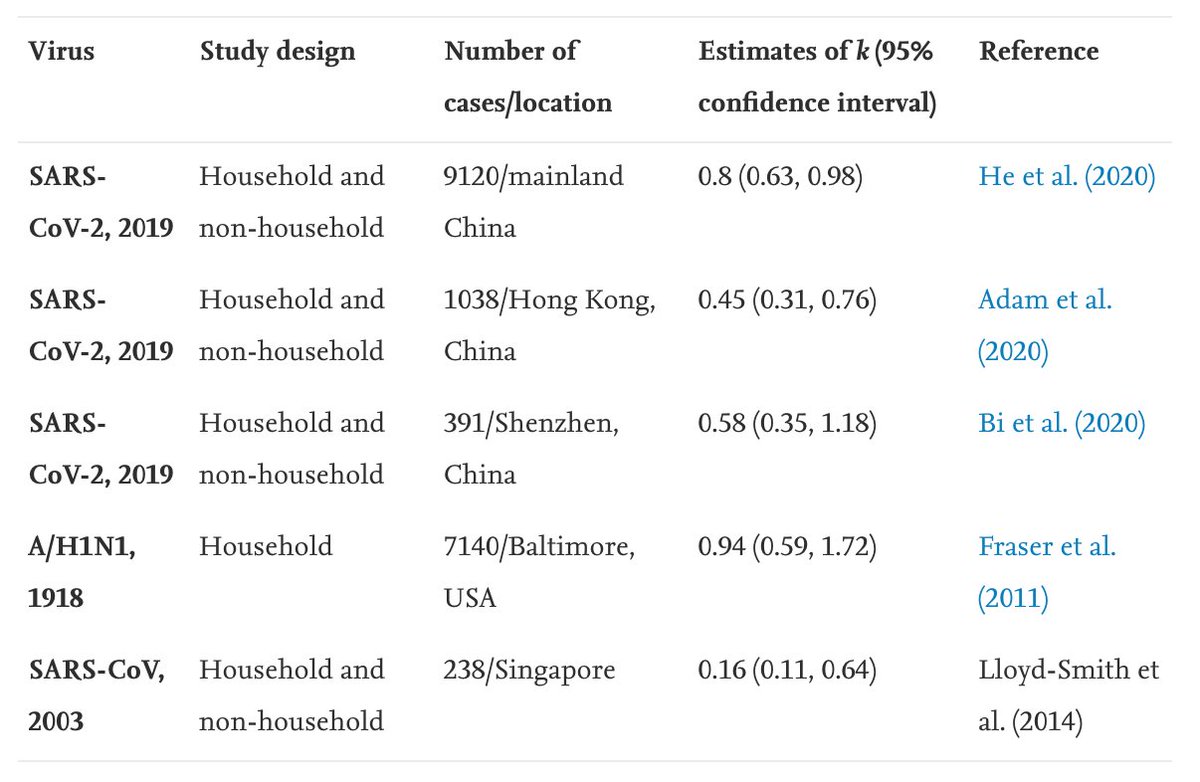
Below report also includes data on secondary attack rate for old UK variants vs new variant VOC 202012/01:
Secondary attack rate measures transmission risk per-contact, so above suggests difference between groups spreading old and new variant isn't down to one group simply having more contacts. This is consistent with data from our recent pre-print (cmmid.github.io/topics/covid19…)
In other words, it seems the new variant VOC 202012/01 has a different ’T’ to the old one.
There may also be some change to 'S' if there are age-specific differences at play (which are yet to be confirmed).

• • •

Missing some Tweet in this thread? You can try to force a refresh
　

Keep Current with Adam Kucharski

Adam Kucharski Profile picture

Stay in touch and get notified when new unrolls are available from this author!

Read all threads

This Thread may be Removed Anytime!

PDF

Twitter may remove this content at anytime! Save it as PDF for later use!

Try unrolling a thread yourself!

how to unroll video
  1. Follow @ThreadReaderApp to mention us!

  2. From a Twitter thread mention us with a keyword "unroll"
@threadreaderapp unroll

Practice here first or read more on our help page!

More from @AdamJKucharski

Adam Kucharski Profile picture
28 Dec
Why a SARS-CoV-2 variant that's 50% more transmissible would in general be a much bigger problem than a variant that's 50% more deadly. A short thread... 1/
As an example, suppose current R=1.1, infection fatality risk is 0.8%, generation time is 6 days, and 10k people infected (plausible for many European cities recently). So we'd expect 10000 x 1.1^5 x 0.8% = 129 eventual new fatalities after a month of spread... 2/
What happens if fatality risk increases by 50%? By above, we'd expect 10000 x 1.1^5 x (0.8% x 1.5) = 193 new fatalities. 3/
Read 5 tweets
Adam Kucharski Profile picture
4 Dec
How different would the global dynamics have been if COVID-19 had instead been a pandemic flu virus with similar fatality rate? A few thoughts... 1/
There are differences between pandemic flu and SARS-CoV-2, of course. In absence of control, serial interval for SARS-CoV-2 (science.sciencemag.org/content/369/65…) is longer than flu (ncbi.nlm.nih.gov/pmc/articles/P…), and evidence SARS-CoV-2 transmission more clustered (sciencedirect.com/science/articl…) 2/
The susceptibility profile may also be different. In flu pandemics, susceptibility is often concentrated in younger groups (pubmed.ncbi.nlm.nih.gov/20096450/) - for COVID-19, severity/susceptibility concentrated in older groups (e.g. nature.com/articles/s4159…). 3/
Read 7 tweets
Adam Kucharski Profile picture
27 Nov
Some locations in Tier 3 had evidence of rising epidemics before November lockdown; others were declining. Same for Tier 1 & 2 – some were rising; some were declining. How come? There are three likely explanations... 1/
First, things like population demography, household structure, and nature of local industry will influence social interactions and hence transmission potential. As a result, baseline R may just be slightly lower in some locations. 2/

Second, high levels of infection will lead to some accumulation of immunity (in short-term, at least). Unlikely it's enough to go back to normal without outbreaks, but could be enough for control measures that would get R near 1 in spring to now get R below 1. (Data from ONS) 3/
Read 7 tweets
Adam Kucharski Profile picture
25 Nov
Relaxing UK COVID-19 control measures over the Christmas period will inevitably create more transmission risk. There are four main things that will influence just how risky it will be... 1/
We can think of as epidemic as a series of outbreaks within households, linked by transmission between households. This is particularly relevant over Christmas, given school holidays and some workplace closures. 2/
We can also think of R in terms of within and between household spread. If the average outbreak size in a household is H, and each infected person in household transmits to C other households on average, we can calculate the 'household' reproduction number as H x C. 3/
Read 8 tweets
Adam Kucharski Profile picture
22 Nov
Some people are interpreting the below study as evidence that people who test positive without symptoms won't spread infection, but it's not quite that simple. A short thread on epidemic growth and timing of infections... 1/
If we assume most transmission comes from those who develop symptoms, there are 2 points where these people can test positive without having symptoms - early in their infection (before symptoms appear) & later, once symptoms resolved (curve below from: cmmid.github.io/topics/covid19…) 2/
So if people test positive without symptoms, are they more likely to be early in their infection or later? Well, it depends on the wider epidemic... 3/
Read 8 tweets
Adam Kucharski Profile picture
12 Nov
Why do COVID-19 modelling groups typically produce ‘scenarios’ rather than long-term forecasts when exploring possible epidemic dynamics? A short thread... 1/
Coverage of modelling is often framed as if epidemics were weather - you make a prediction and then it happens or it doesn’t. But COVID-19 isn’t a storm. Behaviour and policy can change its path... 2/
This means that long-term COVID forecasts don’t really make sense, because it’s equivalent of treating future policy & behaviour like something to be predicted from afar (more in this piece by @reichlab & @cmyeaton: washingtonpost.com/outlook/2020/0…). 3/
Read 9 tweets

Did Thread Reader help you today?

Support us! We are indie developers!

This site is made by just two indie developers on a laptop doing marketing, support and development! Read more about the story.

Become a Premium Member ($3/month or $30/year) and get exclusive features!

Become Premium

Too expensive? Make a small donation by buying us coffee ($5) or help with server cost ($10)

Donate via Paypal Become our Patreon

Thank you for your support!

Follow Us on Twitter!

Like this author's thread?

Get emails when @AdamJKucharski has new unrolls!

Check out other threads from @AdamJKucharski!

Read all threads by @AdamJKucharski