
#統計
amazon.co.jp/dp/4130413007
竹内啓・竹村彰通編
数理統計学の理論と応用
1994
第5章 竹内啓 統計的推測理論の諸問題
に最尤法が漸近的に全然最良でないシンプルな例が載っていたので(添付画像)、#Julia言語 で数値的に確認してみた↓
nbviewer.jupyter.org/gist/genkuroki…
ベイズ統計に繋がる話題。続く

amazon.co.jp/dp/4130413007
竹内啓・竹村彰通編
数理統計学の理論と応用
1994
第5章 竹内啓 統計的推測理論の諸問題
に最尤法が漸近的に全然最良でないシンプルな例が載っていたので(添付画像)、#Julia言語 で数値的に確認してみた↓
nbviewer.jupyter.org/gist/genkuroki…
ベイズ統計に繋がる話題。続く


#統計 その節のタイトルは「5 非正則な場合の漸近推定論」で、尤度函数が漸近的にフラットになる場合(一様事前分布の事後分布が漸近的に一様分布になる場合)のシンプルな例を作っているので、渡辺澄雄『ベイズ統計の理論と方法』の読者は特に興味を持つと思ったので、紹介することにしました。
#統計 データを生成する真の分布は添付画像の密度函数を持つtruncated normal distributionです。標準正規分布を |x|>1 なら確率密度が0になるように改変したもの。
モデルはこの分布を並行移動したものです。パラメータは平均μのみ。
分布の台がパラメータμごとに違うモデルになっている。
モデルはこの分布を並行移動したものです。パラメータは平均μのみ。
分布の台がパラメータμごとに違うモデルになっている。

#統計 その場合に、
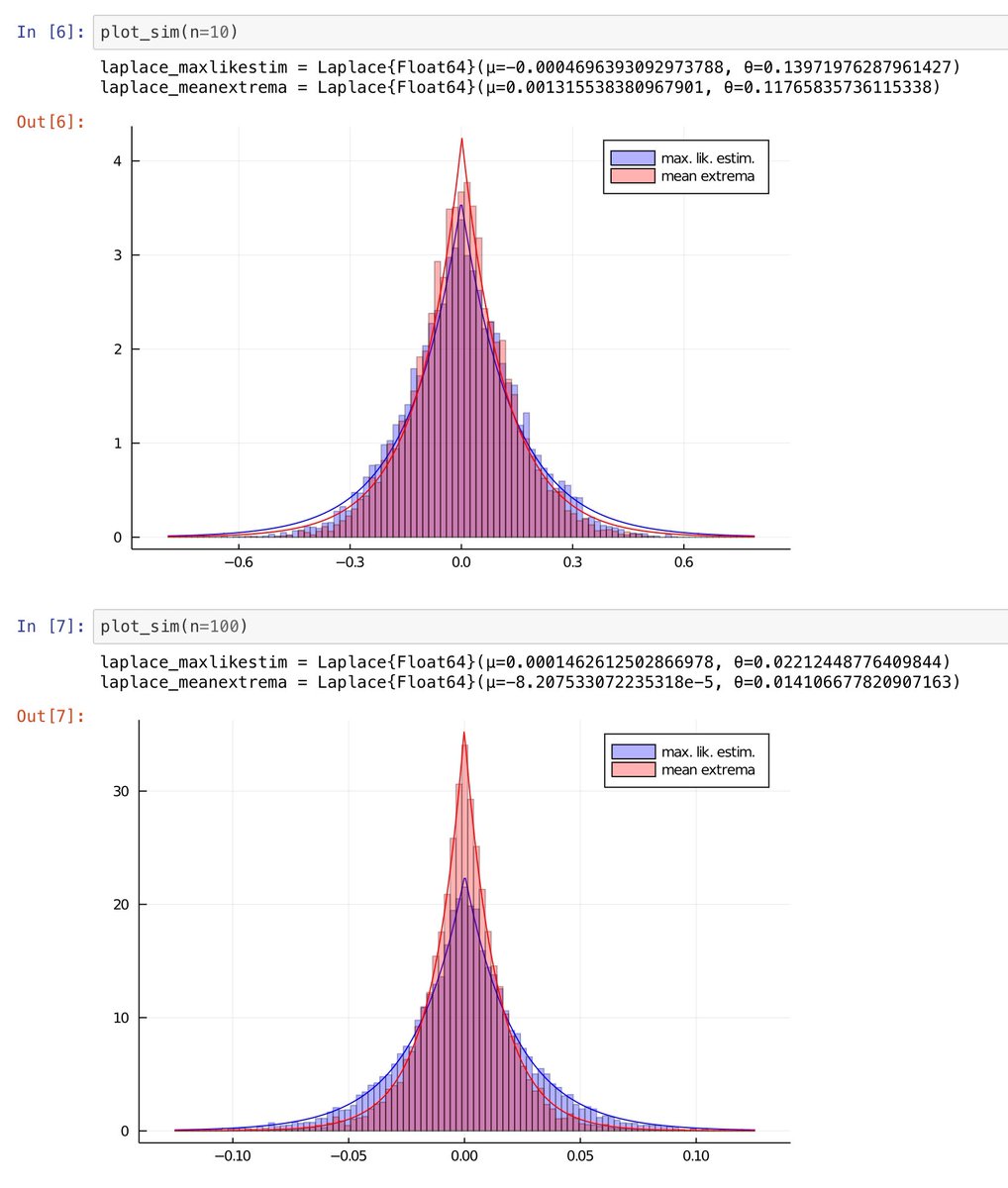
* 最尤法(max.lik.estim.)
* サンプル中の値の最大値と最小値の平均を推定値として採用(mean extrema)
の2つを比較すると、添付画像のように、後者を使った方が真の値の0に近い値が得られる確率が高くなります。
n=10だと違いは小さいにですが、n=100だと違いは明瞭。
* 最尤法(max.lik.estim.)
* サンプル中の値の最大値と最小値の平均を推定値として採用(mean extrema)
の2つを比較すると、添付画像のように、後者を使った方が真の値の0に近い値が得られる確率が高くなります。
n=10だと違いは小さいにですが、n=100だと違いは明瞭。
#統計 #Julia言語 せっかく計算したので n=1000, 10000の場合も。
最尤法(max. lik. estim.)は、最大値と最小値の平均を推定値として採用するシンプルな推定法に惨敗しています。
分散固定のtruncated normal distribution modelでこのようなことが起こるわけです。
最尤法(max. lik. estim.)は、最大値と最小値の平均を推定値として採用するシンプルな推定法に惨敗しています。
分散固定のtruncated normal distribution modelでこのようなことが起こるわけです。

#統計 #Julia言語
nbviewer.jupyter.org/gist/genkuroki…
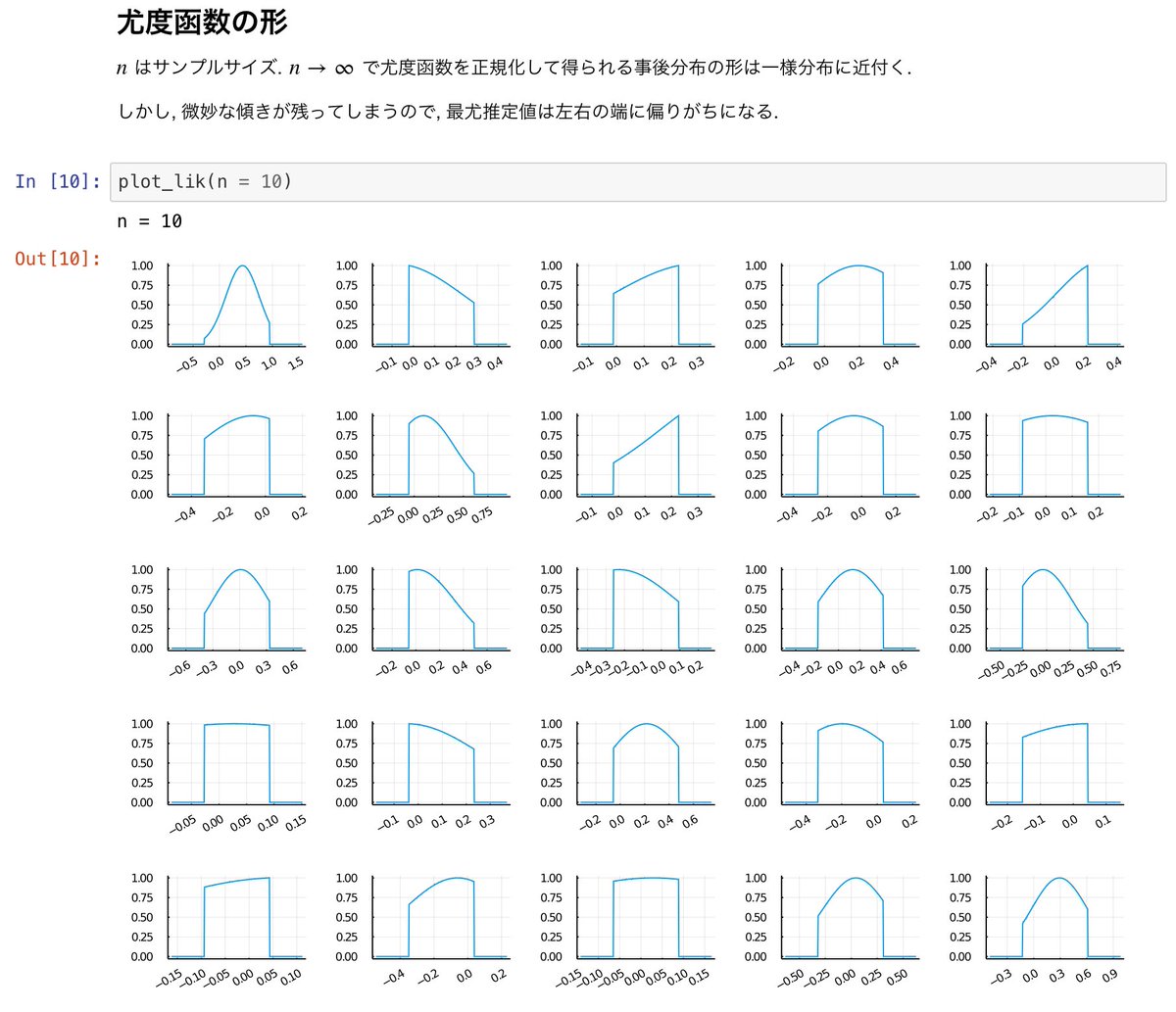
添付画像はランダムに生成したサンプルの尤度函数のグラフです。
n=10, 100, 1000とサンプルサイズnを大きくして行くと、尤度函数が区間上ほぼ一定値の形に近付いて行く様子が見えます。微小な傾きが原因で最尤推定値は区間の両端に偏りがちになる。


nbviewer.jupyter.org/gist/genkuroki…
添付画像はランダムに生成したサンプルの尤度函数のグラフです。
n=10, 100, 1000とサンプルサイズnを大きくして行くと、尤度函数が区間上ほぼ一定値の形に近付いて行く様子が見えます。微小な傾きが原因で最尤推定値は区間の両端に偏りがちになる。


#統計 最尤法が有効なのは、サンプルサイズ大で、尤度函数の形が正規分布の密度函数の定数倍でよく近似される釣鐘型になる場合です。
上の切断正規分布モデルの尤度函数は釣鐘型には全然近付かず、一様分布の密度函数の定数倍の形に近付き、最尤法による推定は全然最良にならない。
上の切断正規分布モデルの尤度函数は釣鐘型には全然近付かず、一様分布の密度函数の定数倍の形に近付き、最尤法による推定は全然最良にならない。
#統計 この場合には、サンプルサイズ大のとき、最尤推定量よりも優れている「サンプル中の最大値と最小値の平均」は平坦事前分布から得られる事後分布の平均値に近似的に等しくなる。
尤度函数が持っている貴重な情報の利用の仕方として、最尤法が最良ではないことは、この例からもわかるわけです。
尤度函数が持っている貴重な情報の利用の仕方として、最尤法が最良ではないことは、この例からもわかるわけです。
#統計 このスレッドのトップで引用した竹内啓さんによる「5 非正則な場合の漸近推定論」の内容は、最尤法が良い方法として使用可能なのは漸近的にベイズ統計の結果と一致する場合で、そうでない場合にはベイズ統計が優れた方法になることを示唆しているとみなせます。
#統計 そこで引用した文献は1994年のものであり、現代においては(少なくとも私にタイムラインでは)
「渡辺澄雄『ベイズ統計の理論と方法』をみんな読んでいる」
という雰囲気になっており、最尤法が最良の方法でない場合にはベイズ統計が良い方法になることを
「みんな知っている」
わけです。
「渡辺澄雄『ベイズ統計の理論と方法』をみんな読んでいる」
という雰囲気になっており、最尤法が最良の方法でない場合にはベイズ統計が良い方法になることを
「みんな知っている」
わけです。
#統計 注意・警告: このスレッドを見て、「最尤法はダメで、ベイズ統計がよい」と解釈した人はひどく誤解している!
最尤法が非常にうまく行く場合は結構あります。そういう場合にはベイズ統計を使う必要はないです。
「ケース・バイ・ケースで自分の目的に合った方法を使う」以上のことは言えない。
最尤法が非常にうまく行く場合は結構あります。そういう場合にはベイズ統計を使う必要はないです。
「ケース・バイ・ケースで自分の目的に合った方法を使う」以上のことは言えない。
#統計 色々な統計モデルの尤度函数のプロットをすると、釣鐘型になって最尤法が非常にうまく行きそうな場合にも多数出会うし、全然釣鐘型にならず、最尤法の使用はやめた方が良さそうな場合にも出会います。
モデルを作るのはユーザー側なので、どの道具をどのように適切に使うかはユーザー側の責任。
モデルを作るのはユーザー側なので、どの道具をどのように適切に使うかはユーザー側の責任。
#統計 一般に、確率密度函数p(x)が p(b)=C>0, p(x)=0 (x>b) を満たすとき、その密度函数で定まる分布のサイズnのサンプルの最大値Mについて、b - M が従う分布は、n大のとき、期待値 1/(nC) の指数分布で近似されます。
真の最大値と標本の最大値の差は1/nのオーダーで小さくなります。
真の最大値と標本の最大値の差は1/nのオーダーで小さくなります。
#統計 一方、真の平均と標本平均の差は、中心極限定理より、1/√nのオーダーでしか小さくなって行きません。
だから、nが大きなとき、標本最大値と比較すると、標本平均の揺らぎの大きさは圧倒的に大きくなる。
これがこのスレッドで紹介した例の理解では重要になります。
だから、nが大きなとき、標本最大値と比較すると、標本平均の揺らぎの大きさは圧倒的に大きくなる。
これがこのスレッドで紹介した例の理解では重要になります。
#統計 確率密度函数
p(x|μ) = const. exp(-(x-μ)²/2) if |x-μ|≤1
p(x|μ) = 0 if |x-μ|>0
のサンプルX_1,…,X_nの尤度函数は、標本平均、標本最小値、標本最大値をそれぞれX̅,A,Bと書くと、
L(μ) = const. exp(-n(μ-X̅)/2) if B-1≤μ≤A+1
L(μ) = 0 otherwise.
p(x|μ) = const. exp(-(x-μ)²/2) if |x-μ|≤1
p(x|μ) = 0 if |x-μ|>0
のサンプルX_1,…,X_nの尤度函数は、標本平均、標本最小値、標本最大値をそれぞれX̅,A,Bと書くと、
L(μ) = const. exp(-n(μ-X̅)/2) if B-1≤μ≤A+1
L(μ) = 0 otherwise.
#統計 nは大と仮定し、p(1|0)=p(-1|0)=C>0とおき、p(x|0)の分散をσ²と書き、サンプルはp(x|0)のサンプルだとする。
このとき、-(B-1)とA+1は期待値1/(nC)の指数分布に近似的に従い、X̅は平均0標準偏差σ/√nの正規分布に近似的に従い、|X̅|≤const./(nC)となる確率は0に近付く。


このとき、-(B-1)とA+1は期待値1/(nC)の指数分布に近似的に従い、X̅は平均0標準偏差σ/√nの正規分布に近似的に従い、|X̅|≤const./(nC)となる確率は0に近付く。



#統計 尤度函数は
L(μ) = const. exp(-n(μ-X̅)/2) if B-1≤μ≤A+1
L(μ) = 0 otherwise
なので、標本平均X̅が、標本最大値-1以上標本最小値+1以下の区間から外れると(n大で外れる確率は1に近付く)、L(μ)を最大化するμは区間の両端のどちらかになります。
L(μ) = const. exp(-n(μ-X̅)/2) if B-1≤μ≤A+1
L(μ) = 0 otherwise
なので、標本平均X̅が、標本最大値-1以上標本最小値+1以下の区間から外れると(n大で外れる確率は1に近付く)、L(μ)を最大化するμは区間の両端のどちらかになります。
#統計 本当は尤度函数の台になっている区間の真ん中あたりがもっともらしいのに、尤度最大化にこだわるとその区間の両端の値を推定値として採用してしまう確率が高くなって、誤差を無駄に大きくしてしまうことになるわけです。
尤度最大化は必ずしも「もっともらしさ」の最大化にはなりません。
尤度最大化は必ずしも「もっともらしさ」の最大化にはなりません。
#統計 「尤度」(ゆうど)は英語のlikelihoodの翻訳語で、英語でlikelihoodは「もっともらしさ」という意味を持っているのですが、数学的に定義された尤度はそのような代物ではないので、likelihoodと名付けた人は尤度について誤解を招く専門用語を作ってしまったことになります。
#統計 #Julia言語 区間[-1,1]の外側を切断した標準正規分布のサンプルの最大値Mについて、1-Mが従う分布が指数分布で近似されることの数値的に確認。
ヒストグラムはモンテカルロ法でのMの分布。
青線はMの正確な分布。
赤の破線は指数分布による近似。
nbviewer.jupyter.org/gist/genkuroki…


ヒストグラムはモンテカルロ法でのMの分布。
青線はMの正確な分布。
赤の破線は指数分布による近似。
nbviewer.jupyter.org/gist/genkuroki…



#数楽 Akahira-Takeuchi (1979)は結局見ていない。
切断正規分布の尤度函数の様子を調べるだけなら、大学新入生レベルの易しい微積分の計算に過ぎない。
しかし、実際には、大学新入生レベルの易しい微積分の計算を自由にできるようになるには、数年以上の修練が必要になる。
数学はかなり大変。
切断正規分布の尤度函数の様子を調べるだけなら、大学新入生レベルの易しい微積分の計算に過ぎない。
しかし、実際には、大学新入生レベルの易しい微積分の計算を自由にできるようになるには、数年以上の修練が必要になる。
数学はかなり大変。
#数楽 大学新入生レベルの微積分だけではなく、線形代数の難易度も同様で、自由に使えるようになるには、数年以上の修練が必要になります。
数ヶ月間勉強して理解できた気分になれなくてもがっかりする必要はなくて、「勉強時間が足りないだけ」(←「だけ」を強調)と考えて気楽に構えた方がお得。
数ヶ月間勉強して理解できた気分になれなくてもがっかりする必要はなくて、「勉強時間が足りないだけ」(←「だけ」を強調)と考えて気楽に構えた方がお得。
#数楽 どうして成立するかが全然理解できない数学的結果を使うときにも、「数年~数十年かけて理解すればいいや」と気楽に構えて、正々堂々と「理解していないことを使っています!」と言ってよいと思います。
そして、同じ「理解していない」であっても様々なパターンがあって同一視はできない。
そして、同じ「理解していない」であっても様々なパターンがあって同一視はできない。
#数楽 「正直かつ気楽」でないと数学の勉強はきつすぎたり、トンデモ化したりします。
「正直かつ常にシリアス」だと神経がすり潰されてアウト。😰
「気楽に不正直」なのは単なる嘘つきです。😅
「正直かつ気楽」以外の道はないと思う。😊
「正直かつ常にシリアス」だと神経がすり潰されてアウト。😰
「気楽に不正直」なのは単なる嘘つきです。😅
「正直かつ気楽」以外の道はないと思う。😊
#統計 平均をμと書くとき、μ±1の外側を切り落とした分散1の正規分布モデルの(真の分布はμ=0に対応)の場合には、異なるμごとに分布の台が異なるせいで、最尤法の予測分布の汎化誤差は確率1で∞になります!
#統計 なぜならば、分布q(x)の台が分布p*(x)の台に含まれないとき、その含まれないq(x)の台内の点をxとするとq(x) > 0, p*(x)=0なので、-q(x) log p*(x) = ∞ となるからです。
こういうことからも、この場合に最尤法は不適切そうであることが分かります。
こういうことからも、この場合に最尤法は不適切そうであることが分かります。
• • •
Missing some Tweet in this thread? You can try to
force a refresh








