Thread by @genkuroki

#Julia言語

Juliaでは

foo(f::函数, X::配列など)

の形式で、配列Xなど(generatorやiteratorを含む)のすべての要素に函数fを施した結果に "foo" の操作を施せる場合が多数あります。

例えばXの要素の絶対値の最大値と和はそれぞれ

maximum(abs, X)
sum(abs, X)

二乗和は

sum(x->x^2, X)

https://twitter.com/genkuroki/status/1348542406291976193

#Julia言語 二乗和は

X = randn(10^6)
sum(Base.Fix2(^, 2), X)
sum(abs2, X)

のようにも書ける。Fix2(f, a)は本質的に x->f(x, a) です。読み易さは x->f(x,a) の方が上のことが多い。

1.96より大きい要素の割合は

count(>(1.96), X)/length(X)

using Statistics
mean(>(1.96), X)

#Julia言語

Xのすべての要素に手続き f を施すには

foreach(f, X)

返り値はforループと同じnothingになります。

Xの要素に函数 f を作用させた結果を集めたものは f.(X) だけではなく

map(f, X)

で作れる。

これら以外にもmaximum, minimum, count, sum, mean, …も似た使用法が可能。

#Julia言語 open(args...; kwargs...) の結果に函数 io -> f(io) を作用させることも

open(f, args...; kwargs...)

の形式で可能です。io -> f(io) の定義が複雑で一回限りしか使わない場合には

open(args...; kwargs...) do io
f(io)の定義
end

がよく使われている。

#Julia言語 m×n行列 A のすべての列(縦⃗ベクトル)に函数 f を作用させた結果を並べた1×n行列は

mapslices(f, A; dims=1)

これをただの1次元配列にしたければ

vec(mapslices(f, A; dims=1))

Aが縦ベクトルの配列なら f.(A) で似たようなことをできますが、同じことを行列でやりたいことは多い。

#Julia言語 foo(f::函数, X::配列など繰り返し可能な何か) のXや for ループのインデックスの動く範囲に使えるものが非常に多彩であることを知るには

methods(iterate)

の結果を眺めるとよいです。

〇〇について△△を繰り返すことをやらせたい場合には、このスレッドの内容が役に立つ。

#Julia言語 #数楽 #統計

〇〇達について互いに独立に△△を実行するプログラムのコードを書くことは易しい場合が多く、並列化も易しい。

しかし、△△の実行が各〇〇ごとに独立になっていない場合は面倒になり、効率的な並列化も難しくなる。

確率論でもi.i.d.だと話が易しくなる。

#Julia言語

サンプル A の経験累積確率分布函数

ecdf(A, x) = count(≤(x), A)/length(A)

using Distributions してあれば

ecdf(A, x) = mean(≤(x), A)

でもよい。ブロードキャストで使う場合には配列AをRefで保護する。

x = range(0, 6; length=600)
y = ecdf.(Ref(A), x)

#Julia言語

using Base64
showimg(mime, fn; tag="img") = open(fn) do f
base64 = base64encode(f)
display("text/html", """<$tag src="data:$mime;base64,$base64" />""")
end

showimg("image/jpeg", "foo.jpeg"; tag="img width=80%")

でJupyterノートブック上に画像を取り込める。

#Julia言語

open(f -> ファイル f を読み込んで行う操作, ファイル名)

と等価な

open(ファイル名) do f
ファイル f を読み込んで行う操作
end

の形式のコードはよく書く。

1つ前のツイートの内容はこれの応用例。

#Julia言語 確率分布 dist における確率変数(函数) f(X) の期待値 E[f(X)|X～p] のモンテカルロ法による計算は

X = rand(dist, L)
mean(f, X)

例えば、ガンマ分布でのlog Xの期待値は

α, θ = 10, 0.1
using Distributions
dist = Gamma(α, θ)
L = 10^7
X = rand(dist, L)
ElogX_mc = mean(log, X)

#Julia言語 サンプルX上でのf(x)の平均が

mean(f, X)

とシンプルに書けるのはありがたい。

このスレッドのテーマはこれの一般化がJuliaで広範に使用可能になっているという話。これを知っていると、数学語の直訳でJuliaのコードを書ける場合が増える。しかも多くの場合に計算速度的にも効率的。

#Julia言語 微訂正

❌E[f(X)|X～p]
⭕️E[f(X)|X～dist]

モンテカルロ法による近似で十分なら

E[f(X)|X～dist]
↓
X = rand(dist, L)
mean(f, X)

と翻訳できる。対応が見易い。

確率変数Xはモンテカルロ法では乱数列Xに対応。逆にこのイメージで確率変数を(測度論を経由せずに)理解してもよい。

https://twitter.com/genkuroki/status/1348784642153828353

#Julia言語 分布Gamma(α, θ)におけるlog xの期待値は

1/(θ^α Γ(α)) ∫_0^∞ e^{-x/θ} x^{α-1} log x dx
= (∂/∂α)log(θ^α Γ(α))
= log θ + ψ(α)

と書ける。ここでψ(s)=(log Γ(s))'はディガンマ函数と呼ばれる基本特殊函数で、適当なライブラリを使えばコンピュータで気楽に計算できる。

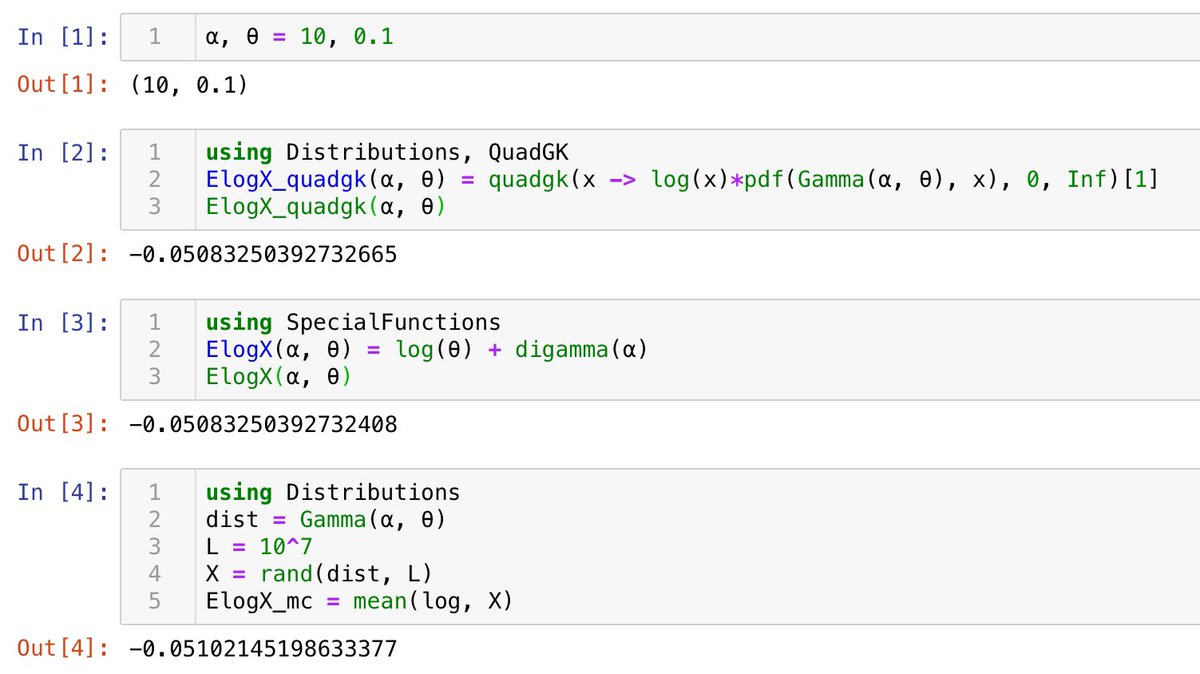
#Julia言語 実1変数函数の数値積分は QuadGK.jl パッケージが定番だと思う。

自分で下手に数値積分のコードを書くより、これを利用した方が計算が速いことが多い。

許容誤差を大きめにして計算時間を減らしたければrtol=1e-3とかに設定して使えばよい。

github.com/JuliaMath/Quad…