I built a model to predict whether you'll be involved in a crash next time you get in a car.
And it's 99% accurate!
Allow me to show you...π
And it's 99% accurate!
Allow me to show you...π
Here is the model:
π
π
The National Safety Council reports that the odds of being in a car crash in the United States are 1 in 102.
That's a probability of 0.98% of being involved in a crash.
Therefore, my silly model is accurate 99% of the time!
See? I wasn't joking before.
π
That's a probability of 0.98% of being involved in a crash.
Therefore, my silly model is accurate 99% of the time!
See? I wasn't joking before.
π
By now, it is probably clear that using "accuracy" as the way to measure the predictive capability of a model is not always a good idea.
The model could be very accurate... and still, give you no useful information at all.
Like right now.
π
The model could be very accurate... and still, give you no useful information at all.
Like right now.
π
Determining whether you are crashing on a car is an "imbalanced classification problem."
There are two classes: you crash, or you don't. And one of these represents the overwhelming majority of data points.
Takeaway: Accuracy is not a great metric for this type of problem.
π
There are two classes: you crash, or you don't. And one of these represents the overwhelming majority of data points.
Takeaway: Accuracy is not a great metric for this type of problem.
π
Crashing a car is a little bit too morbid, so here are a few more problems that could be framed as imbalanced classification tasks as well:
β«οΈ Detecting fraudulent transactions
β«οΈ Classifying spam messages
β«οΈ Determining whether a patient has cancer
π
β«οΈ Detecting fraudulent transactions
β«οΈ Classifying spam messages
β«οΈ Determining whether a patient has cancer
π
We already saw that we can develop a "highly accurate" model if we classify every credit card transaction as not fraudulent.
An accurate model, but not a useful one.
How do we properly measure the model's effectiveness if accuracy doesn't work for us?
π
An accurate model, but not a useful one.
How do we properly measure the model's effectiveness if accuracy doesn't work for us?
π
We care about *positive* samples (those transactions that are indeed fraudulent,) and we want to maximize our model's ability to find them.
In statistics, this metric is called "recall."
[Recall β Ability of a classification model to identify all relevant samples]
π
In statistics, this metric is called "recall."
[Recall β Ability of a classification model to identify all relevant samples]
π
A more formal way to define Recall is through the attached formula.
β«οΈ True Positives (TP): Fraudulent transactions that our model detected.
β«οΈ False Negatives (FN): Fraudulent transactions that our model missed.
π
β«οΈ True Positives (TP): Fraudulent transactions that our model detected.
β«οΈ False Negatives (FN): Fraudulent transactions that our model missed.
π
Imagine that we try again to solve the problem with the attached (useless) function.
We are classifying every instance as negative, so we are going to end up with 0 recall:
β«οΈ recall = TP / (TP + FN) = 0 / (0 + FN) = 0
π
We are classifying every instance as negative, so we are going to end up with 0 recall:
β«οΈ recall = TP / (TP + FN) = 0 / (0 + FN) = 0
π
That's something!
Now we know that our model is completely useless by using "recall" as our metric.
Since it's 0, we can conclude that the model can't detect any fraudulent transactions.
Ok, we are done!
Or, are we?
π
Now we know that our model is completely useless by using "recall" as our metric.
Since it's 0, we can conclude that the model can't detect any fraudulent transactions.
Ok, we are done!
Or, are we?
π
How about if we change the model to the attached function?
Now we are returning that every transaction is fraudulent, so we are maximizing True Positives, and our False Negatives will be 0:
β«οΈ recall = TP / (TP + FN) = TP / TP = 1
Well, that seems good, doesn't it? π
π
Now we are returning that every transaction is fraudulent, so we are maximizing True Positives, and our False Negatives will be 0:
β«οΈ recall = TP / (TP + FN) = TP / TP = 1
Well, that seems good, doesn't it? π
π
A recall of 1 is indeed excellent, but again, it just tells part of the story.
Yes, our model now detects every fraudulent transaction, but it also misclassifies every normal transaction!
Our model is not too *precise*.
π
Yes, our model now detects every fraudulent transaction, but it also misclassifies every normal transaction!
Our model is not too *precise*.
π
As you probably guessed, "precision" is the other metric that goes hand in hand with "recall."
[Precision β Ability of a classification model to identify only relevant samples]
π
[Precision β Ability of a classification model to identify only relevant samples]
π
A more formal way to define Precision is through the attached formula.
β«οΈ True Positives (TP): Fraudulent transactions that our model detected.
β«οΈ False Positives (FP): Normal transactions that our model misclassified as fraudulent.
π
β«οΈ True Positives (TP): Fraudulent transactions that our model detected.
β«οΈ False Positives (FP): Normal transactions that our model misclassified as fraudulent.
π
Let's compute the precision of our latest model (the one that classifies every transaction as fraudulent):
β«οΈ TP = just a few transactions, so a small number
β«οΈ FP = (1 - a small number) = large number
β«οΈ precision = TP / (TP + FP) = small / large β 0
π
β«οΈ TP = just a few transactions, so a small number
β«οΈ FP = (1 - a small number) = large number
β«οΈ precision = TP / (TP + FP) = small / large β 0
π
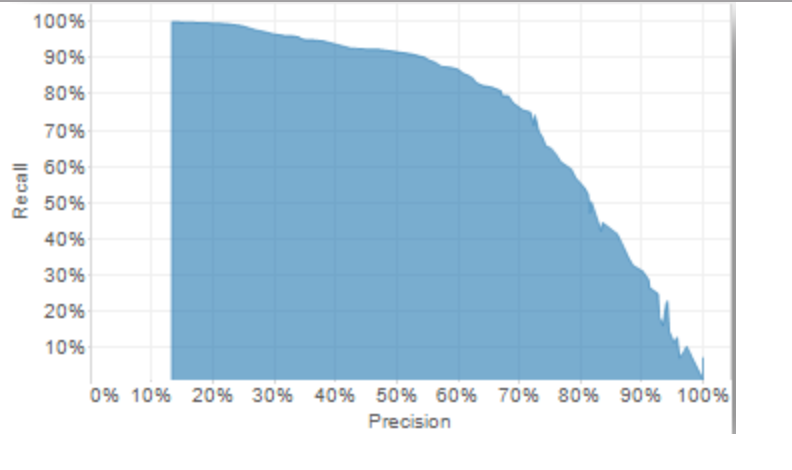
The precision calculation wasn't that clean, but hopefully, it is clear that the result will be very close to 0.
So we went from one extreme to the other!
Can you see the relationship?
As we increase the precision of our model, we decrease the recall and vice-versa.
π
So we went from one extreme to the other!
Can you see the relationship?
As we increase the precision of our model, we decrease the recall and vice-versa.
π
Alright, so now we know a few things about imbalanced classification problems:
β«οΈ Accuracy is not that useful.
β«οΈ We want a high recall.
β«οΈ We want high precision.
β«οΈ There's a tradeoff between precision and recall.
There's one more thing that I wanted to mention.
π
β«οΈ Accuracy is not that useful.
β«οΈ We want a high recall.
β«οΈ We want high precision.
β«οΈ There's a tradeoff between precision and recall.
There's one more thing that I wanted to mention.
π
There may be cases where we want to find a good balance between precision and recall.
For this, we can use a metric called "F1 Score," defined with the attached formula.
[F1 Score β Harmonic mean of precision and recall]
π
For this, we can use a metric called "F1 Score," defined with the attached formula.
[F1 Score β Harmonic mean of precision and recall]
π
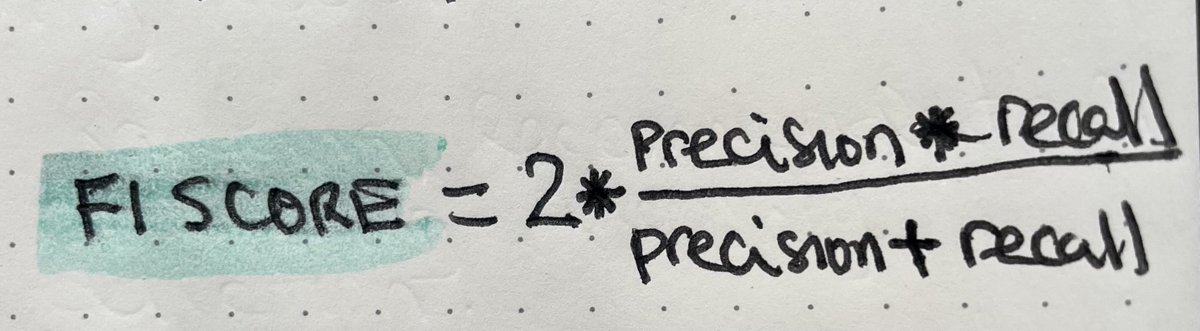
The F1 Score gives equal weight to both precision and recall and punishes extreme values.
This means that either one of the dummy functions we discussed before will show a very low F1 Score!
My models suck, and they won't fool the F1 Score.
π
This means that either one of the dummy functions we discussed before will show a very low F1 Score!
My models suck, and they won't fool the F1 Score.
π
So that's it for this story.
If you want to keep reading about metrics, here is an excellent, more comprehensive thread about different metrics used in machine learning (and the inspiration for this thread):
If you want to keep reading about metrics, here is an excellent, more comprehensive thread about different metrics used in machine learning (and the inspiration for this thread):
https://twitter.com/AlejandroPiad/status/1356716242606972931?s=20
β’ β’ β’
Missing some Tweet in this thread? You can try to
force a refresh
γ
