Thread by @YorickB

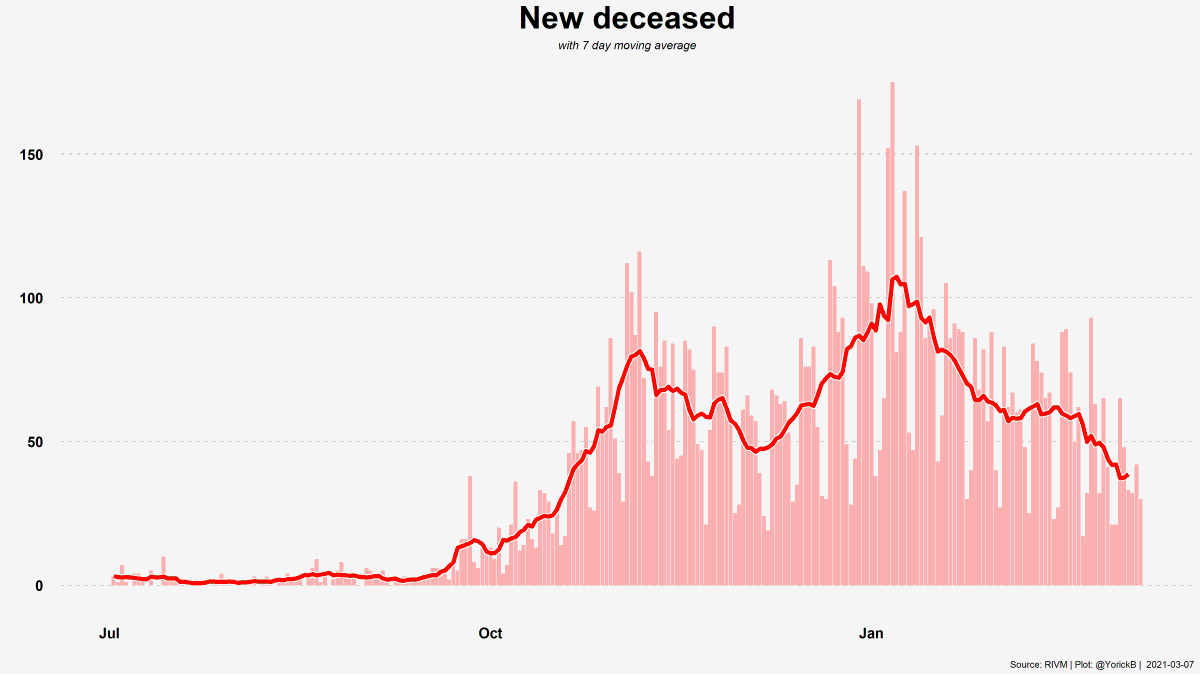
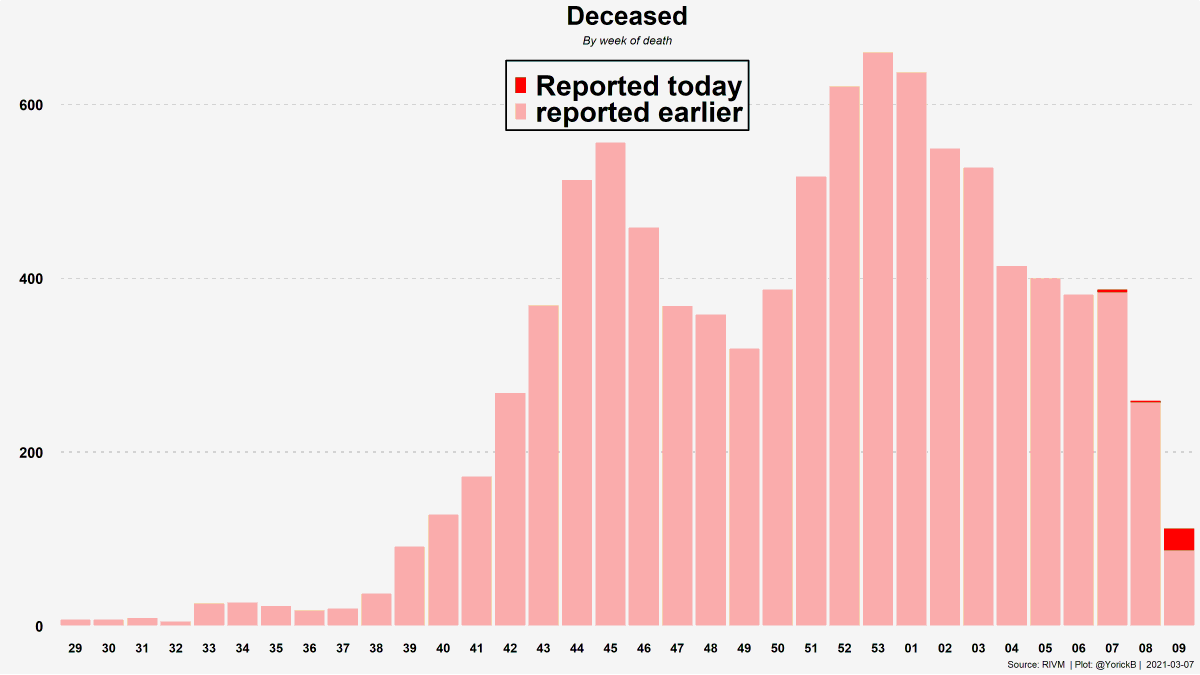
🧵Het grote "Not-at-All-Safe-zone" draadje.🧵

In dit draadje ga ik proberen het onderstaande plaatje te doorgronden.

Misschien is dit al wel het "Nomogram", maar ik denk het niet.
Morgen zal Van Dissel het toelichten, en kijken we of ik het goed had.🤓

Het is al heel vaak gezegd: als je nú een maatregel instelt, of juist versoepeld, zie je pas daarvan het effect 2 weken later in het aantal besmettingen en ziekenhuis opnames.

Dit is het bekende: sturen op de achteruitkijkspiegel effect.

Van Dissel laat dit zien in onderstaande grafieken.
1) R is onder de 1, en er komen versoepelingen --> R boven de 1.
2) We zien de eerste effecten op de IC 2 weken later, en nemen gelijk maatregelen.
3) Voordat je weer dat effect ziet, neemt de bezetting (enorm) toe.

Van Dissel heeft er voor de zekerheid ook een achteruitkijk spiegel in getekend 🪞. 😊

Scenario:
Je begint met 200 mensen op de IC, versoepeld op dag 10; en de R gaat naar 1,5 --> je verwacht op dag 30 al een bezetting te hebben van 300. Als je dan pas maatregelen neemt (gaan in op dag 32) zal de IC bezetting toch nog doorstijgen naar een bezetting van 1.200 (!)

En hier de hele slide voor de mensen die alle parameters even willen bekijken:

Dit is natuurlijk een model; en in theorie kun je zelf heel veel waardes kiezen. En op basis daarvan krijg je andere uitkomsten. Aangezien er plaatje van staat, neem ik aan dat het RIVM dit intern aan het testen is.

(En dankzij een Kamermotie krijgen wij het misschien ook!🥳)

Maar goed, als je dus aan die knoppen gaat zitten, kun je dus inschatten:
1) start met 200 bedden, R van 1.1 --> piekbezetting van ~500.
2) start met 500 bedden, R van 1.25 --> piekbezetting van ~1.300.
3) start met 300 bedden, R van 1.75 --> piekbezetting van ~1.800 (#codezwart)

Nu we dit allemaal weten krijgen we het plaatje met de "Not at all safe-zone" Die ik zelf niet helemaal snap... 🤣

(Het helpt niet mee dat de y-as logaritmisch is.)

Maar ik ga een poging doen om het te begrijpen zonder hulp 😎

Dat komt ie...

Oké ik snap het! 🥳

Als je 750 mensen hebt op de IC (1a), met een R van 1.00 blijft het aantal op 750. (geel is 750)

Als je een kleine 250 mensen op de IC hebt bij een R van 1.30, verwacht je een piek van 750. --> Het gele bolletje bij (2).

Maar als je voor die zelfde toename in de R van 1.30 gaat kijken naar een begin bezetting van 500 bedden, verwacht je een toename naar 1.500 bedden (bij 3, rode lijn)

Aangezien we nu zo'n 500 mensen op de IC hebben, en de R van de UK variant 1.14 is verwacht je (zonder versoepelingen) tussen de 1.000 en 1.3000 bezette bedden. (3de golf)

En dan komen we uit op het plaat je in het begin.

Het OMT adviseert de piekbelasting niet hoger te laten worden dan 750 covid patienten op de IC.

Als we dus ontzettend willen versoepelen, kan dat; maar alleen als er minder dan 100 covid patienten op de IC liggen. (log schaal)

Dus... duidelijk!
- Er is een "save zone" waar we bijna uitvallen.
- De IC bezetting moet omlaag
- In dit hele verhaal heeft niemand bedacht: wat als we nou eens de R eens ónder de 1 houden? 🤷‍♂️

Dit ís sturen op IC capaciteit. ⤵️

(En nu even klappen voor de zorg👏👏👏)

[einde]

[bron]
rijksoverheid.nl/onderwerpen/co…

[morgen technische briefing]

Draadje OMT advies -->

https://twitter.com/YorickB/status/1369039197680582660?s=20

[nabrander]

Als de R onder de 1 blijft, komt er géén piek, en zit je áltijd in de safe-zone.
Ik heb even ene plaatje gemaakt van de zone waar je wilt zitten. Dat is dus het groene vlak. Waar IC bezetting niet uitmaakt, want de R is kleiner dan 1. -->de IC bezetting daalt altijd.

@innouveau maakte een nóg beter versie!

https://twitter.com/innouveau/status/1369269954126749696?s=20