Thread by @genkuroki

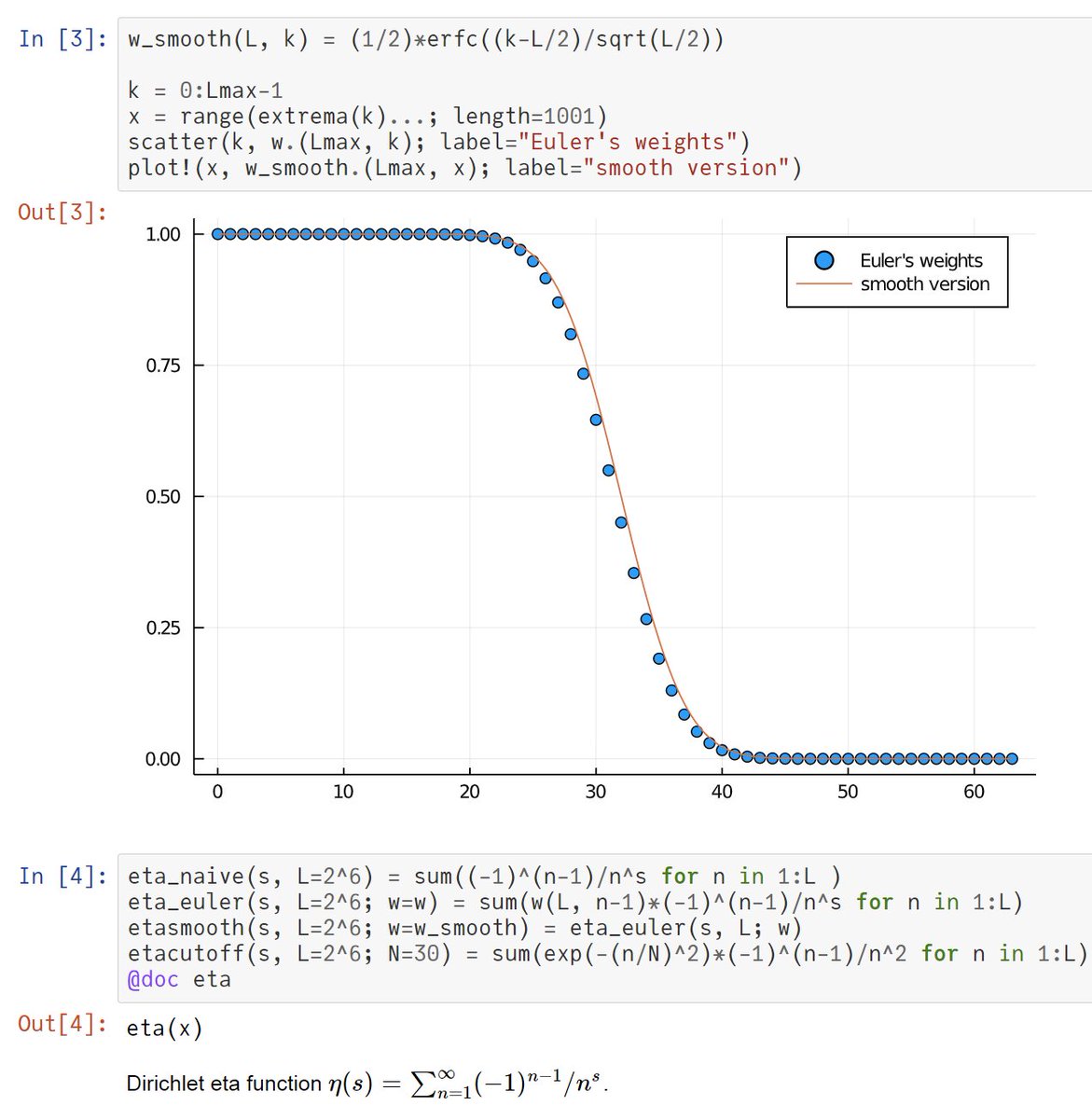
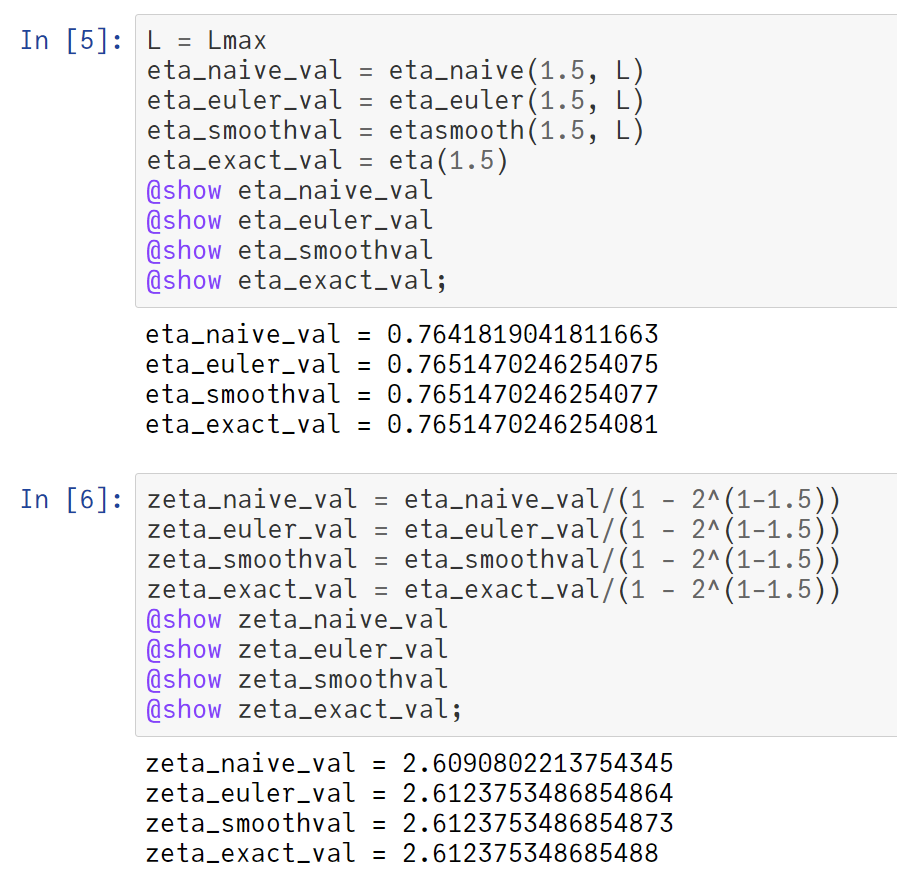
#Julia言語 リポジトリの方の公式マニュアルに以下が追加されましたね。

* 引数の型の過剰な制限はよくある間違いです。疑わしいなら引数の型を書くのをやめましょう。

* Juliaでは戻り値の型宣言はほとんど使われません。一般に「型安定」な函数を書くべきです。

github.com/JuliaLang/juli…

#Julia言語 具体的には

fib(n::Int) = n ≤ 2 ? one(n) : fib(n-1) + fib(n-2)

はよくある間違で、

fib(n)::Int = n ≤ 2 ? one(n) : fib(n-1) + fib(n-2)

も誤りです。どちらでもBigIntによる計算が不可能になる。よく分からないなら

fib(n) = n ≤ 2 ? one(n) : fib(n-1) + fib(n-2)

でよい。

#Julia言語 無用に引数の型を制限してしまううようだと、NASAでは仕事をできなくなります。(NASAでもJuliaを使っている)

https://twitter.com/genkuroki/status/1371100742078005250

#Julia言語

function f(x::型名) ～ end

と引数の型を書く場合には型名として最も広い抽象型を選ぶ。よく分からなかったら、型名は省略するべき。

不適切に返り値の型を

function f(x)::型名 ～ end

と指定してしまう問題については以下のリンク先を参照。

https://twitter.com/genkuroki/status/1372488887788920832

#Julia言語 「型名を書かなければいけない」「型名は書いた方がよい」「型名を書いた方が安全になる」という(一般には正しくない)考え方を過学習してしまっていることに気付くことも、Juliaを使うメリットの1つだと思います。

あとクラスを使うOOPスタイルへの過剰適応に気付くためにもよい。

#Julia言語 おまけ：グローバル変数を引数を経由せずに直接函数内で使ったり、

struct Foo
a
b
end

のように書くと、計算がひどく遅くなります。

struct Foo{S, T}
a::S
b::T
end

なら大丈夫。

多くの場合にmutable structではなく、structを使った方がお得。

#Julia言語 関連↓
discourse.julialang.org/t/why-specify-…

#Julia言語 Juliaでは函数の引数の型宣言の機能は多重ディスパッチで使われる。

引数の型宣言はコードを読み易くするためにも使えるのですが、引数の型の過剰な制限(よくある間違い)を引き起こすようではまずい。

"""
f(x)のxは実数
"""
function f(x)
～
end

のように書いておけばよいと思う。

#Julia言語 典型的な過学習は以下のリンク先で確認できる。

f(x::Int)::Int = x/2 のように::Intを付けてもJuliaはコンパイル時に返り値がIntになることをチェックしてエラーを出してくれません。f(2)はコンパイルされて正常に実行されてしまう。f(1)は実行時エラー。

discourse.julialang.org/t/why-specify-…

#Julia言語 は明らかに「新しいこと」もしくは「昔からあったが広く普及していなかった技術を一般ユーザーに届くようにすること」をしています。

そこに広く普及している技術への過学習を持ち込んでコメントしても無意味で、「新しいこと」を学んだ方がお得。

トレードオフで考えることが基本。

#Julia言語 Juliaでは、予想外のバグを取るために型宣言は役に立たず、@ code_warntype や @ code_typed で型情報の伝搬の仕方を見ることが役に立ちます。

その自動化の方向での素晴らしい成果(開発進行中)が

github.com/aviatesk/JET.jl

です。こういう新しい試みをみんなで応援して行くべき。