Thread by @genkuroki

#数楽

多項式f∈ℝ[x]に「a∈ℝをf(a)∈ℝを対応させる函数」を対応させる写像は単射なので、多項式fとそれに対応する実数の函数を区別しなくも大丈夫。(無限体でもOK)

有限体F上の多項式g∈F[x]に「a∈Fをg(a)∈Fを対応させる函数」を対応させる写像は単射でないので、それらを同一視できない。

#数楽 例えば二元体𝔽₂={0,1} (1+1=0)について、𝔽₂上の多項式としてxとx²は異なるが、𝔽₂上の函数としてはどちらも恒等写像になって等しくなってしまう。

xとx²を𝔽₂の2次拡大𝔽₄=𝔽₂[α] (α²=α+1)上の函数とみなしたものは互いに異なる。

こういう具体例がノータイムで出て来ることが大事。

#数楽 面倒なのは有理函数(多項式環の分数体の要素)に対応する「函数」の場合。

有理函数ごとに定義域も変わるので、異なる定義域を持つ函数達を同時に扱うための「処理」が必要になる。(これには複数の処方箋がある。)

結果的に、無限体の場合には、有理函数と対応する「函数」は同一視可能になる。

#数楽 そもそも中学校の数学の教科書では、2つの文字式(有理函数の場合もある)がいつ等しくなるかについて、はっきりした説明はないと思います。

以前、私が見た教科書では、2つの文字式が等しいとはどういうことかに関する説明を見つけることはできませんでした。

#数楽 どうせ無限体上の多項式や有理函数しか扱っていないのだから、それらと通常の函数の区別を厳密にする必要はないと思います。(その辺に関するミスリーディングな説明に注意！)

しかし、中学校の数学の教科書では多項式函数として等しいことがどういう意味であるかの説明も見つけられなかった！

#数楽 その辺については、中学校の学習指導要領解説(≠学主指導要領、厳密に区別すること！)にもひどく不明瞭な説明があってひどいことになっています。

おそらく数学が苦手な人達の数学教育業界ではそのひどいやつが標準化している。

https://twitter.com/genkuroki/status/1219329237577912320

#超算数 「操作の方法」「操作の結果」という説明の仕方がひどく曖昧で悲惨なことになっている。

数学の言葉を使って明瞭に説明せずに、独特の説明で全国の中学校数学教師に悪影響を与える方針。

ひど過ぎ。

https://twitter.com/genkuroki/status/725243585138806784

#超算数 「多項式函数」ブームの元ネタはこれか！

有理函数を函数とみなすときの定義域は有理函数ごとに変わる。

例えば、有理函数1/xを函数とみなすときには0を除外しなければいけないが、有理函数x²/xは多項式xになるので函数とみなすときに0を除外しなくてよい。

本質的にこれだけの話。

https://twitter.com/mike_twinkle/status/1374735721659953153

#数楽 無限体上で考えていれば、多項式と多項式函数は自然に同一視されるので、多項式と多項式函数の区別を真面目に行う必要は必ずしもない。

一方、多項式分の多項式(=有理函数)を函数とみなすときには分母が0になる点を除外しなければいけないが、除外される点達は有理函数ごとに違うので要注意。

#数楽 あと、この手の問題について、「高校の範囲でマルになるようにする」とか、「純代数的に扱う」という無用に狭い考え方をする必要はない。

考え方を制限した途端に多くの直観が失われる。

極限や漸近挙動を見るという発想も非常に大事です。

#数楽

2/(x² - 1) = a/(x - 1) + b/(x + 1)

という等式を見たら、「x→1で両辺がどのように振る舞うか」などもイメージできるということを知っておいて損がないです。

x→1とすると 2/(x²-1)=1/(x-1) 2/(x+1)とa/(x-1)の中の1/(x-1)の因子の絶対値は幾らでも大きくなる。続く

#数楽 b/(x+1)の項は相対的にちりのようなものになり無視できる。x→1では巨大になる 1/(x-1) の因子を除いた 2/(x+1) と a が一致しなければいけない。すなわち1=aでなければいけない。

同様にx→-1で2/(x-1)とbが一致するので-1=bでなければいけない。

実際にa=1, b=-1を代入して確認すれば終了。

#数楽 代入できなくても、極限が収束しなくても、漸近挙動(振る舞い方)を直観的に考えることはできる。

もちろん、曖昧な直観だけではなく、確固たる論理的基盤もあった方が良いのだが、直観がないのも困ると思う。

#数楽

2/(x²-1) = a/(x-1) + b/(x+1)

の両辺にx-1をかけて

2/(x+1) = a + b(x-1)/(x+1)

として、xに1を代入して

1 = a

を得てもよい。

この議論と両辺にx-1をかける前の状態でx→1としたときの様子をイメージすることを比較せよ。

#数楽 注意：数学用語の習慣で、有理函数は多項式分の多項式を意味し、写像としての函数を意味しません。

だから「有理函数を函数とみなす」という言い方が合法的になる。

数学用語にはこの手のものが結構多いです。

もちろん、適当な処理のもとで有理函数は通常の函数ともみなされます。

日本語に訳すときに失敗するパターンもあって、行列も行列式もどちらも式なのですが、行列と行列式は違う式になります(笑)

今さらdeterminantを「行列式」と呼ばずに済ますのは難しい。

人の名前が付いている数学用語にもひどい場合があって、A. BorelさんはKilling form (Killingは人の名前)という数学用語を作ったのですが、Killing formの概念を作ったのはKillingさんではんし。しかもBorelさんは後でそのように名付けた理由を覚えていないと言っている(笑)

en.wikipedia.org/wiki/Killing_f…

最近の中学校数学では、言葉を覚えさせるようなことが増えた点がかなりひどいと思う。

言葉を覚えるという思考法は数学からは程遠い考え方だと思う。

単に権威的な価値しかない用語群を覚えさせる行為はやめた方がよい。

#数楽 例えば、x²/x を函数とみなすときの定義域については

① x²/x=xであり、xを函数とみなすときには定義域から0を除外する必要はない

と考えて良いだけではなく、

②x²/xを函数とみなすときにx=0を除外したとしても、連続函数としてx=0まで一意的に拡張できる

と考えても良いです。続く

#数楽 続き。数学的に真っ当な考え方は無数にあることが多く、それらの多くが結果的に同等の結果を与える場合がある。上の①と②は同等に結果を与えます。

バツをつけて良い理由をいきなり考えることは、非教育的かつ非数学的行為だと思います。

#数楽 少々間違っていても、一部に論理的なギャップがあっても、少しの訂正で十分な議論になる場合は、数学的に立派な議論であり、中高生が「不十分だが、立派な議論」を(たとえ偶然であっても)しているのを見つけたら、いい気になる程度に徹底的に褒めてやった方が数学教育はうまく行くと思います。

#数楽 当たり前の話なんですが、論理的厳密さの追求は「試験でバツをつけたり、減点するため」にやっているわけではありません。

細部が曖昧で論理的な基礎付けが不十分であるように見える素晴らしいアイデアを確固たるものにするために論理的厳密さを追求しているのです。

#数楽 数学では、論理的にはギャップのある素晴らしいアイデアや直観を大事にするために論理的厳密さの追求が行われているのです。

論理的にはギャップのある素晴らしいアイデアや直観を潰すために論理的厳密さの追求を利用する人には「地獄に落ちろ」と言ってよい。

#数楽 中高生では以上で述べたようなことを理解するのは難しい。

だから、論理を「潰すため」ではなく、「活かすため」に使う場面を教える側は生徒に見せることが必要。

「この答案を書いたやつは分かっていないに違いない」という態度を安易に表に出す奴は数学教育の世界から出て行くべき。

関連

「数学的に正確に考えればどうなるか」

に関する議論を省略して、

「どのように採点するべきか」

の議論にしてしまうことは、数学教育的に有害だと思います。

率直に言って不快なので注意した方が良いと思う。

まずは教える側が十分に数学を理解していないとお話にならない。

https://twitter.com/genkuroki/status/1215784041825226752

ℚ[√x] の取り扱いの話。

まずは中学生に教えている側が、中学生が文字xの √x を十分な論理的な裏付けなしに使ったときに、やろうと思えばどのようにギャップを埋められるかを理解している必要がある。

教えている側が数学を理解しておらず、理解していないことに無自覚なのは完全にアウト。

https://twitter.com/genkuroki/status/1215788854365392896

数学は難しいので教える側が数学を理解していないことまでは許されて然るべきだと思う。

しかし、自分自身が数学を全然理解していないことに無自覚で、中高生による野生の立派な議論を救えていない可能性に無自覚なのは相当にまずい。

まさにそれ。

「高校生はそこまで考えていない。だからバツにした方が教育的によい」というようなひどい考え方をしている人達には相当に問題がある。

https://twitter.com/kamo_hiroyasu/status/1374914147528310787

無限体上で考えていれば、適切に定義された多項式函数全体の集合は元の多項式環と同型な環になるので、元の多項式環における定理群は多項式函数全体のなす環でも意味を持ちます。

多項式環と多項式函数の区別の必要性を極度に強調するのはミスリーディング。この点にはみんなもっと注意した方がよい。

#超算数 あと、そもそも、中学校で習う文字式について等式がいつ成立するかについて、論理的に明瞭な説明が教科書にない点も問題だと思っています。

例えば

x²/x = x

が成立する理由はどこに書いてあるのか？

こういう基本的なことさえ不明瞭。

私が見逃しているだけなのかもしれない。情報募集。

#超算数 「中学校数学」や「高校数学」といった独特の考え方を含む分野が、一般数学ユーザーが標準的に使っている数学とは別に作られて、教えられるようになっているという問題がある。

単項式は多項式ではないことにしたり、多項式ではなく整式と言うような分野が維持され続けている。

#超算数 中学校の数学の問題

①x²/x=xが成立する理由は教科書のどこに書いてありますか？

②ab÷abの解釈には((ab)÷a)bと(ab)÷(ab)の少なくとも2つがあり得るのですが、どれであるかを確定させるための演算の優先順位の説明は教科書のどこに書いてありますか？

どちらも書かれていないんじゃない？

私は、有限体を扱っていないのに「多項式と多項式函数を区別しないのが悪い」と強調した人達は微妙にダメな発言をしたと思っています。有理函数の扱いが面倒という問題はある。

現実には「それ以前の問題」も生じていると思う(1つ前のツイートを参照)。根本的な所がまずい。

文字式の取り扱いは中学校で本格的に習うのですが、文字式がいつ等しくなるのかの明瞭な説明がないままで、先に進んで行くスタイルになっていて、習っている中学生の側は形式的な記号操作だけをわけもわからずやらされている場合が多いと思う。

「移項」という教え方でさらに被害を拡大している感じ。

ほとんどあらゆる用語が要注意で、例えば元ネタの問題文中にある「恒等式」は、「方程式」と対になっていて、「等式は恒等式と方程式に分類される」のようなおかしな言説を構成する用語の1つになっています。

慎重に中高生に数学を教えたい人は安易に使わない方が良い用語の1つになっていると思う。

ちょー算数問題というのがあって、まともな算数とは異なる独自の非常識な算数もどきの体系(ちょー算数)を算数教育界は100年以上かけて育てて来ていて、算数の教科書は非常識なちょー算数を教えるように編集執筆されています。

それに近い問題が中高の数学教育にもある。これは大問題だと思います。

現代の標準的な数学のスタイルでは、等式は単に等しいことを意味するに過ぎず、「等式は恒等式と方程式に分類される」というのはナンセンス極まりないのですが、中高生にそのように説明したがっている人達がいる。

等式のような最も基本的な事柄でさえまともに説明されていない。

そう！その問題もある。

「因数分解」のような用語の説明も極度に曖昧で困ったことになっている。

数学をよく理解している人にとっても、意味が確定しないような説明しかされていないのが普通というのは問題あり過ぎ。

数学を理解していれば意味が確定する程度にが明瞭に説明して欲しいと思う。

https://twitter.com/mathworld4/status/1375271157272772608

文字式とは何かについて中学校の学習指導要領解説(学習指導要領そのものとは異なる文書、厳密に区別せよ！)によれば

【abやa/b ，さらに，a＋b，a−bという表現は，操作の方法を表しているとともに，操作の結果も表している】

らしい。この部分の説明が曖昧過ぎてひどい。

https://twitter.com/genkuroki/status/725243585138806784

【操作の方法を表しているとともに，操作の結果も表している】のような説明の仕方は、標準的な数学とは異なる独自の体系を作って教えようとする数学教育の専門家の間ではよく使われているらしい。

数学的な基本概念が数学教育の世界では別のものに上書きされていることを常に疑う必要があります。

やってはいけないことは、勝手に忖度して解釈・擁護してしまうことです。これが実に多い。中高生相手の教育の文脈と違って、相手は専門家とみなされるべき人達です。

○○という数学教育の専門家が××と言っていた(書いていた)の類の情報は正しいことの証拠として採用できないことにも注意が必要。

* 操作の方法 ↦ 函数
* 操作の結果 ↦ 函数の値

と解釈しようとしても

【例えば，３a＋２や５x−５のように演算記号が残ったままにしておくことに違和感をもつことがあるので，このことに十分に留意する】

と書いてあることから、3a+2や5x-5も「操作の結果」の例になっていることが分かります。

算数・数学教育界には「答え」という標準的な数学にはない独自の概念があります。「操作の結果」は「答え」を意味しているらしい。

数式を整理するときには、単に目的に合わせて便利な形に整理するだけで、整理の結果は目的のために使えれば何でも良い。これが普通の数学の運用の常識。

そういう常識に反する「答え」という概念が算数数学教育界で横行してしまっている。

例えば、「1/√2 は分母を有理化していないので、正しい答えではない」のように「答え」というろくでもないもの概念が使用されているのです。

しかも「答え」の明瞭な定義はどこにも書かれていない。

そういう曖昧で有害な概念である「答え」を「専門的」には「操作の結果」のように言うことがあるらしいのです。

こういう感じで、ろくでもない曖昧な考え方に独自の用語を与えて権威化して、学習指導要領解説(≠学習指導要領そのもの)に載せて、影響力を発揮している人達がいるのです。

公的な算数数学教育の具体的な中身を、数学的におかしな考え方をしている「専門家集団」が社会的に堅固な地位を築いて遂行しているという事実にみんな気付くべき。

そういう人達の名前が表に出ることは少ないので、ターゲットが絞り難くなっている点も問題。

かなり深刻な問題なんです。

「専門家集団」が独自の算数数学もどきの体系を作ってしまっているという問題は表に出難いです。

大学の教育学部で使われている算数数学教育関係の教科書を見たことがあって、さらに算数や数学の教科書のマニュアル本(教師用指導書、一般人購入不可)の内容に目を通したことがないと、気付かない。

ツイッターで教科書のマニュアル本の内容について教えてもらって、自分でも大学での算数数学教育の講義で使われている本を購入して色々確認するまで、「専門家集団」レベルで非常識な考え方をしていることに全く気付いてなかったです。

これに偶然に気付くのは至難の技だと思う。

数学教育について大学で講義を受けた人達は、多項式や有理函数についての正確な理解を得るのではなく、

文字式は【操作の方法を表しているとともに，操作の結果も表している】

というような曖昧で意味不明の説明を受けて、これが権威ある正しい考え方だと思っている可能性が高い。

因数分解についても、ℤ[x]とℚ[x]における素元分解の違いを認識してから、中学校で数学を教える人は少数派だと思います。

数学は難しいのでそのこと自体を悪いとは思いませんが、因数分解についての初めて教えるときにℤ[x]とℚ[x]における素元分解の違いを勉強できるようになっていないとまずい。

まとめ

* 算数数学教育界は100年以上かけて標準的な数学とは異なる独自の非常識で曖昧な算数数学もどきの体系を育てて来てしまっている。

* 標準的な数学の理解は数学の教員養成課程の教育で優先事項になっていない。

これを逆転させるにはどうすればよいのか？

私も色々細かいことも述べましたが、多項式やら有理函数のような普通の数学の話をできるだけで、算数数学教育に関する話としては「天国」に分類されてしまうと思います。マジで天国。

現実には「0を倍数から除くのが普通」のような考え方の「専門家」が教育の世界で影響力を持っていたりします。

#超算数

8254.teacup.com/kakezannojunjo…
【新訂数学1 新興出版社啓林館．昭和53年
～0はすべての整数の倍数であるが，倍数・約数については，0は除いて考えることにする”】

中学校の数学。

「0はすべての整数の倍数であるが，倍数・約数については，0は除いて考えることにする」？？？

何が言いたい？？

https://twitter.com/takusansu/status/1372160973147049985

これは大問題。

仮に50%の人が数学教育界の伝統のせいで落ちこぼれさせられているという現状があるとして、仮にそれを継続的に48～49%までに減らせたとします。

すると落ちこぼれさせられずに世に出る人数が年に1～2万人のオーダーで増える。経済成長にも影響する可能性があるかも。

「天国」な話題に戻る(笑)

「有理式」と「有理関数」という用語を区別したい気持ちは分かるのですが、慣習的にはそれらを区別しないことが多いです。

だからコミュニケーションを円滑にするには、有理式と有理函数を勝手に違う意味にしない方がよいです。

続く

添付画像は岩波数学辞典第4版より

https://twitter.com/4p_t/status/1374973742963589120

あと「暗黙の前提を廃して厳密な議論をしたい」のであれば、例えば 1/x を函数とみなすときの定義域の定義の説明を略して「恒等式」という用語を使っている問題文の側に批判的であるべきです。

暗黙のうちに 1/x の定義域を{x∈ℝ|x≠0}とみなすのが当然だと思う人には厳密な議論は無理だと思う。

https://twitter.com/4p_t/status/1374973742963589120

「どのような値を代入しても」の部分がかなり曖昧ですよね。

例の等式が多項式や有理函数として成立することと整数点での値がすべて等しくなることは同値なので(後者の例では±1を除く)、「どのような値を代入しても)の部分を曖昧にしても害は小さいという主旨なのかな？

数研出版の教科書数学IIより

https://twitter.com/4p_t/status/1374992605373558787

「多項式として等しい」とか「ℝ²上の函数として等しい」とか「{x∈ℝ|x≠0}上の函数として等しい」と言えば、函数の定義域を明確に定義せずに「恒等式」という用語の使用を避けられるのに、わざわざそのように説明しているということは、厳密な議論をする気がないことを意味しています。

厳密な議論を放棄するスタイルが明瞭な文言を引用して、厳密な議論の足しにしようとするのはちょっとおかしい。

あと、この件では、批判の対象は、問題を出した側、教科書の記述、教える側の態度の方であるべきです。

中途半端な所で厳密にしようとすると、数学的本質を見失います。

例えば、a/x+b/(x-1)の函数としての定義域を仮に{x∈ℝ|x≠0,1}とし、1/xの函数としての定義域を{x∈ℝ|x≠0}としたとします。

このとき、a/x+b/(x-1)と1/xは定義域が異なる函数なので、それらは函数としては絶対に等しくなりません！

有理函数の函数としての取り扱いで面倒なのはここです。続く

定義域の違う2つの函数 a/x+b/(x-1) と 1/x を比較するときには、定義域の共通部分で比較することになります。

論理的に厳密な議論をする場合には、そのような函数の比較の仕方が何らかの意味で「整合性」を持っていることを保証しておく必要があります。(同値関係になっているかとか)

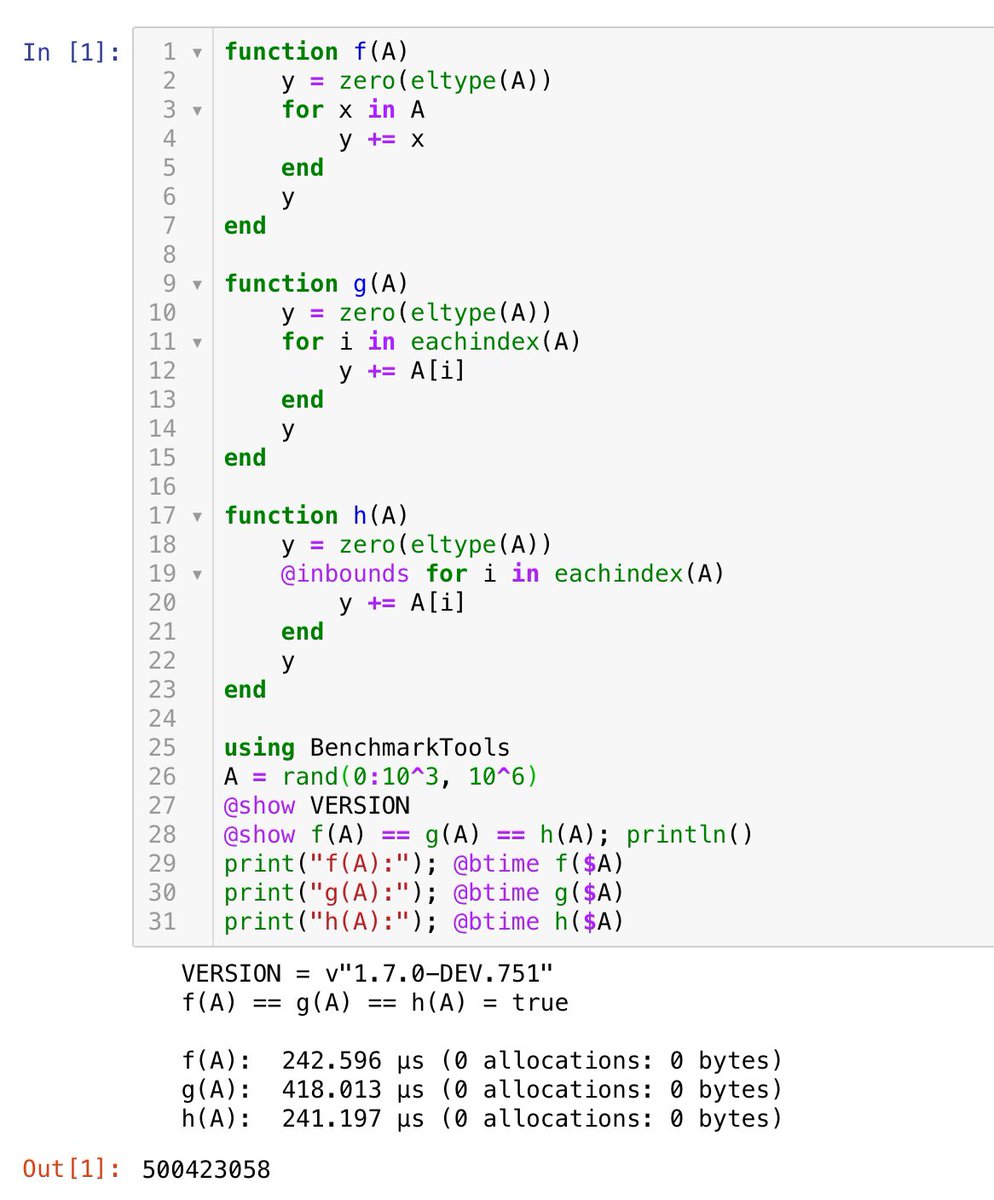
例えば、添付画像のような場合には、定義域の共通部分上で f = g と g = h がそれぞれ成立していても、定義域の共通部分上で f ≠ h となることが普通にある。

有理函数を函数とみなして比較する場合にはこのような問題が生じない。そのお陰で非常にお気楽にいー加減な議論の多くが正しくなる。

基礎づけの段階で論理的につめておけば、それ以後は、イーカゲンにも見える議論がすべて正しい議論として素通しになる場合がある。

論理的な厳密さにはこういう御利益がある。

論理的な厳密さにどういう御利益があるのかについて何も触れずに、うれしい御利益と無関係な所で、「理解していないとみなすため」とか「採点でバツをつけることを正当化するため」に論理的厳密さの要求を使うことは、数学的にはおかしな行為だし、教育的にはさらに問題があると思います。

例えば、a(x),b(x),c(x),d(x)∈ℂ[x]、b≠0、d≠0から有理函数 f(x)=a(x)/b(x), g(x)=c(x)/d(x) を作ったとします。

n=deg(a(x)d(x)-b(x)c(x))とおく。

ℂ[x]の商体の元としてf(x)=g(x)

⇔ ℂ[x]の元としてa(x)d(x)=b(x)c(x)

⇔ 任意のα∈ℂについてa(α)d(α)=b(α)c(α)

続く

さらに、

⇔ n+1個以上のα∈ℂについてa(α)d(α)=b(α)c(α)

⇔ n+1個以上のα∈ℂについてb(α)≠0かつd(α)≠0かつf(α)=g(α)

⇔ 任意のα∈ℂについてb(α)≠0かつd(α)≠0ならばf(α)=g(α)

教える側は知っていて、このレベルの話を高校生に要求するのはやめた方がよいという話。

くだらない「恒等式」とやらの「定義」に基くことを要求するのはやめた方がよい。

元ネタの

2/(x² - 1) = a/(x - 1) + b/(x + 1)

について、「x=±1でどうなっているか？」と考えることはむしろ「普通」の考え方なので、色々指導した結果、そういう発想が高校生の心の中から消えてしまうようだと、相当に酷いことをしたことになると思います。

分母を払って

2=a(x+1)+b(x-1)

となったときに、x=±1とおくと計算が簡単になると気付く人の方が、曖昧な「恒等式」の定義に機械的に忠実であろうとする人よりも優れていると思います。

曖昧な「恒等式」の定義に忠実であろうとする人であっても、x→±1の極限を考えることはできる。

a/(x-1)+b(x+1)+(c+dx)/(x²+1)=(px³+qx²+rx+s)/(x⁴-1)

を満たすa,b,c,dをp,q,r,sで表す問題でも分母を払って、x=±1,±iを代入すれば簡単。暗算で可能なレベル。

同等の

a/(x-1)+b(x+1)+c/(x-i)+d/(x+i)=(px³+qx²+rx+s)/(x⁴-1)

を考えてもよい。

a/(x-1)+b(x+1)+(c+dx)/(x²+1)=(px³+qx²+rx+s)/(x⁴-1)

を満たすa,b,c,dをp,q,r,sで表す問題で、分母を払った後に、x=±1,±iを代入することに躊躇するようになってしまった人は、

　自分自身がダメな数学教育の被害者であることを自覚

して、次の世代に被害を拡大しないようにするべき。

算数数学教育に関する話題では「ダメな教育の被害者が教える側に立ったときに加害者側にまわる」というパターンが実に多い。

「ダメな教育」については、職業的には私自身にも責任があって、数学における論理的に厳密な議論の重要性の位置付けについて適切に伝えることに失敗して来たのではないかと思っています。(この話は結構繰り返している。私だけの問題ではない。)

再度強調しておくけど、件の元ネタの状況は標数0で無限体上の話だとみなされるので、多項式と多項式函数を同一視して何も問題が生じない場合になります。

これは数学的事実であり、議論の余地はない。続く

これも繰り返しになるが、有理函数=有理式=多項式環の商体の要素を函数とみなすときのめんどくささの話をしていればよかったと思う。続く

さらに、有限体上の多項式環𝔽_q[x]の要素をそれから自然に決まる𝔽_q上の函数と同一視できない点を指摘して、多項式を多項式函数と同一視できないと安易に言ってしまうのもまずい。

なぜならば、𝔽_q[x]の要素は代数閉包𝔽̅_q上の函数とは自然に同一視でき、実際にそうするパターンが多いからです。

多項式を単なる抽象的な環の要素とみなすだけではなく、函数ともみなせる方が数学的な考え方は豊かになります。

有限体上の場合には確かに注意は必要ですが、定義域を代数閉包まで広げれば多項式と多項式函数を同一視できるし、実際にそうすることが便利な場合があります。

安易に考えたら「○○できねえ」となったとしても、実際には適切な設定のもとでは○○することができて便利ならば、たとえ高校生にすぐに理解できなさそうな話であっても正直に「できます」「便利です」と言わないとまずいと思います。