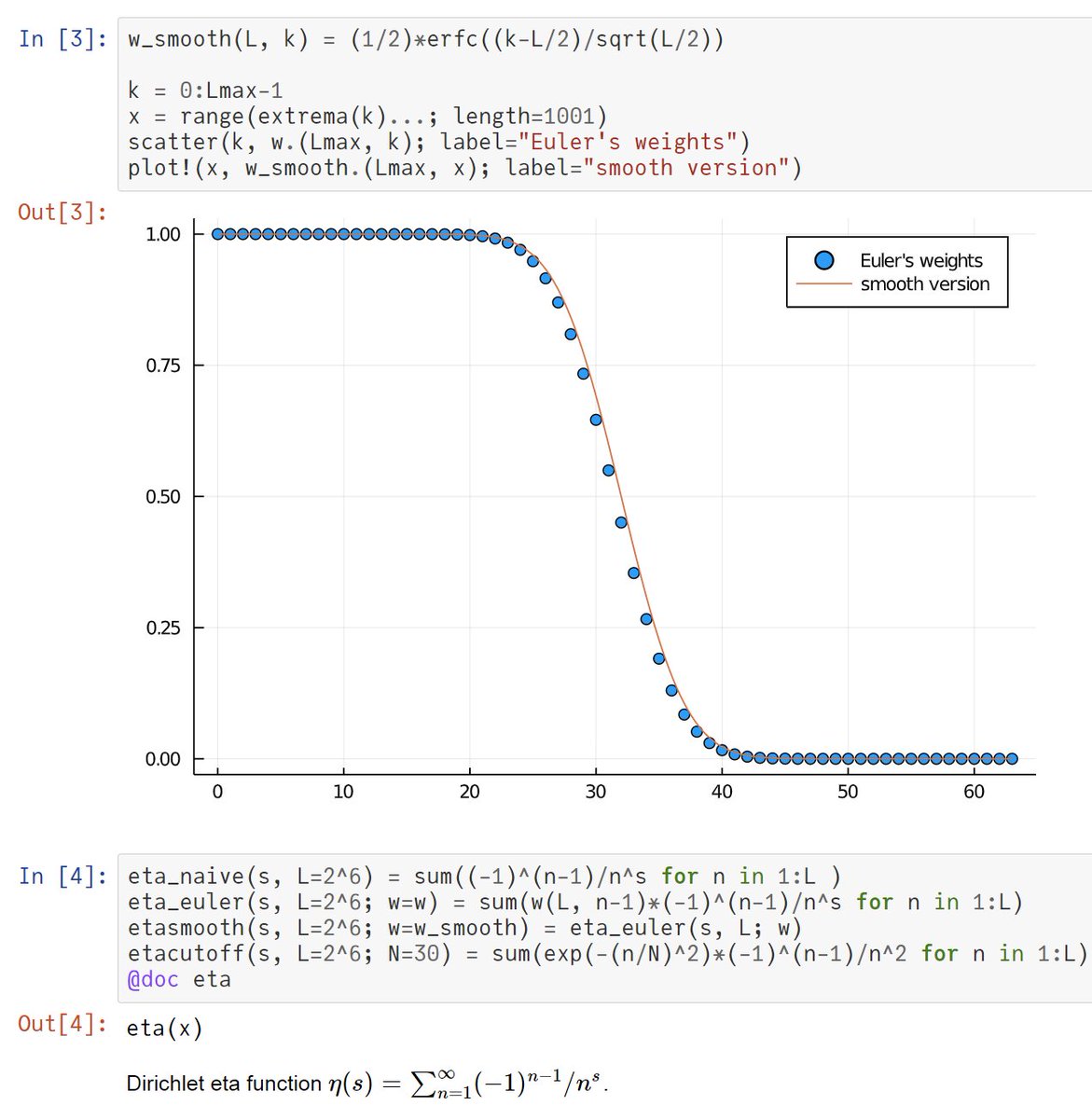
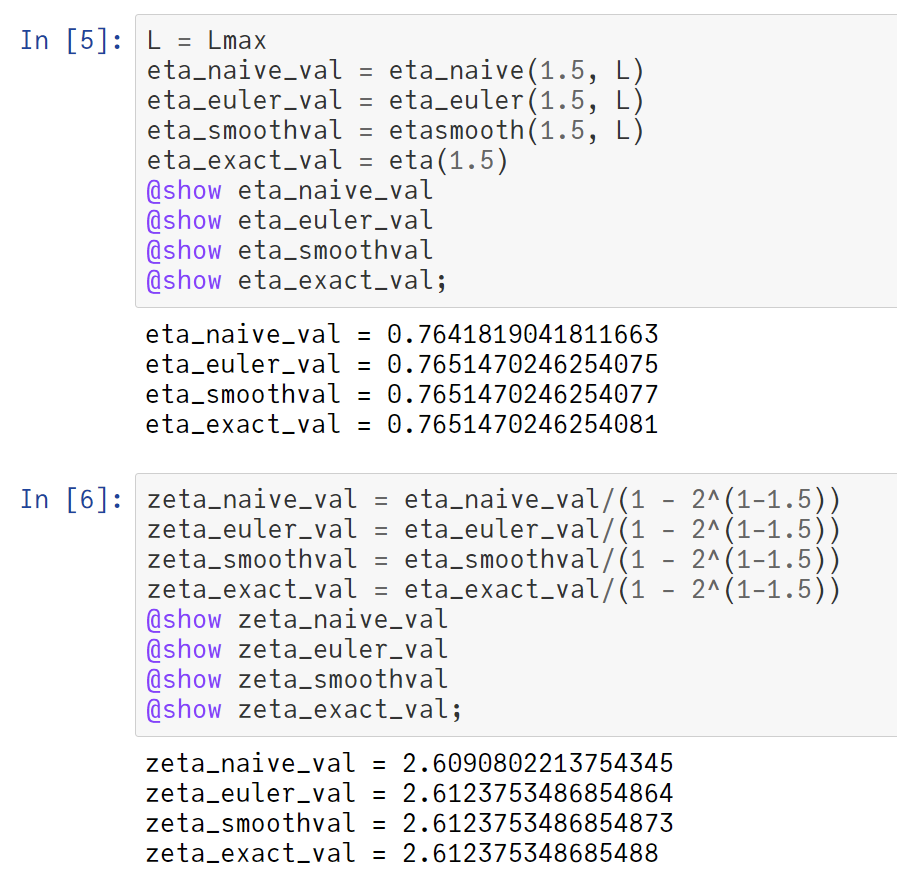
大学生相手であっても、必要な数学の実力は結構高いので、統計学を教えるのに苦労しています。
高校生相手に検定が「お墨付きが得られる道具」であるかのように教えられてしまうようになったら最悪。
あと、信頼区間がモデル依存であることも(大学生と同様に)教えることにならないと思う。
高校生相手に検定が「お墨付きが得られる道具」であるかのように教えられてしまうようになったら最悪。
あと、信頼区間がモデル依存であることも(大学生と同様に)教えることにならないと思う。
https://twitter.com/hirokazuohsawa/status/1374861536057991170
現実には世界的にかなり悲惨なことになっていて、論文を日常的に書いている研究者であっても、統計的検定を「お墨付きが得られる道具」扱いしている人達が沢山いるんじゃないか?
そういう現状は若くて優れた研究者が育つことを妨害していると思う。
こういう問題を維持固定しないような教育が必要。
そういう現状は若くて優れた研究者が育つことを妨害していると思う。
こういう問題を維持固定しないような教育が必要。
まだ高校生なのに、「統計的に有意である!」を水戸黄門的な「ひかえおろう!」と同じ意味で使うようになったら最悪(笑)
#統計 簡単な確率を計算できる能力抜きに、統計学を理解できるはずがない。
例えば、表と裏が等確率で出るコインを10回投げたとき、表の回数が2回以下になる確率を求められないなら完全にアウト。
高校で統計学を無理に教えずに、統計学を見据えた確率の話をしっかり教えた方がうまく行くと思う。
例えば、表と裏が等確率で出るコインを10回投げたとき、表の回数が2回以下になる確率を求められないなら完全にアウト。
高校で統計学を無理に教えずに、統計学を見据えた確率の話をしっかり教えた方がうまく行くと思う。
https://twitter.com/hirokazuohsawa/status/1374896489160302592
#統計
統計学をまともに(=無害な形で)理解するためには、ある程度以上の数学的実力が必須。
そして、実際の使い方を学ぶためには、数学以外の事柄に関するしっかりした教養が必要。
あと、大学生向けの統計学の教科書の内容も結構ひどい場合があることを理解できるレベルの人が教える必要がある。
統計学をまともに(=無害な形で)理解するためには、ある程度以上の数学的実力が必須。
そして、実際の使い方を学ぶためには、数学以外の事柄に関するしっかりした教養が必要。
あと、大学生向けの統計学の教科書の内容も結構ひどい場合があることを理解できるレベルの人が教える必要がある。
これ、大学の先生でコメントした方が良い人達がツイッターにも結構いるんじゃないか?
直接制度設計に関わったことがない人であっても、大学で統計学の講義をする仕事もしたことがある人なら(多分苦労しているはず)、高校数学への統計の導入の仕方が強引すぎることのまずさは明らかだと思う。
直接制度設計に関わったことがない人であっても、大学で統計学の講義をする仕事もしたことがある人なら(多分苦労しているはず)、高校数学への統計の導入の仕方が強引すぎることのまずさは明らかだと思う。
https://twitter.com/hirokazuohsawa/status/1374896489160302592
#統計 コインの表と裏がそれぞれ1/2の確率で出て、さらに10回のコイン投げが独立になるという仮想的なモデルの中で確率を計算している、という理解の仕方ができないと、統計学の理解は出発点から非科学的でめちゃくちゃなものになっちゃうんだよね。
数学的モデルの中での確率計算になっている。
数学的モデルの中での確率計算になっている。
#統計 現実と無関係に、数学的モデルを考えることができることを納得するためには、まず数学的抽象化に耐える数学的実力が必要で、さらに科学的な常識も身に付けていないといけない。
多分、大学生向けの統計の講義でもこの辺を理解してもらうことはあんまりうまく行っていない。
多分、大学生向けの統計の講義でもこの辺を理解してもらうことはあんまりうまく行っていない。
#統計 検定におけるP値は、数学的モデルの中における確率の近似値の一種で、現実において起きる可能性が高いとか低いと言うときの確率ではない。
95%信頼区間の95%も同様で、数学的モデルの中における確率の近似値でしかない。モデルが現実で妥当でなければ95%という数値も現実において妥当ではない。
95%信頼区間の95%も同様で、数学的モデルの中における確率の近似値でしかない。モデルが現実で妥当でなければ95%という数値も現実において妥当ではない。
#統計 博士号を取った人であっても、「仮に現実でサンプルを何度も取り直して、95%信頼区間を繰り返し計算し直したならば、その中で真の値を含むものの割合は95%程度になる」と教科書通りに誤解していることがあります。
95%信頼区間の95%はモデル内における割合でしかないことを忘れている。
95%信頼区間の95%はモデル内における割合でしかないことを忘れている。
#統計 数学的モデル内部での値を計算しているだけなのに、その値を現実における値だと混同してしまうことは、モデルと現実の混同という典型的に非科学的な考え方をしているわけです。
博士号を取っていてもそういう非科学的な統計学(しかも初歩的な区間推定)の理解の仕方しかできていない場合がある。
博士号を取っていてもそういう非科学的な統計学(しかも初歩的な区間推定)の理解の仕方しかできていない場合がある。
#統計 多分、金銭が絡む仕事で統計学の技術を使った人なら、モデルと現実の混同はないと思う。
モデルを使った統計的な予測が結構外れることが分かっていても、その道具を使った方が仕事全体の効率を統計的に上げてくれる可能性がある。こういう使い方が実際には多いのではないか?
モデルを使った統計的な予測が結構外れることが分かっていても、その道具を使った方が仕事全体の効率を統計的に上げてくれる可能性がある。こういう使い方が実際には多いのではないか?
#統計 それに対して、P値や95%信頼区間の95%については誤解が非常に多い。
誤解が多くなる理由はP値や95%信頼区間を「お墨付きを得るための手段」だと思っているから。
モデル内数値に過ぎないもので「お墨付き」が得られるはずがないので、モデル内数値に過ぎないことを無視し易くなる。
誤解が多くなる理由はP値や95%信頼区間を「お墨付きを得るための手段」だと思っているから。
モデル内数値に過ぎないもので「お墨付き」が得られるはずがないので、モデル内数値に過ぎないことを無視し易くなる。
#統計 多分、検定や信頼区間を「お墨付きを得るための手段」だと誤解している人は、統計モデリング(最尤法やベイズ法を使う)にまで「お墨付きを得る方法」を求めて、どこまで行ってもおかしな考え方から抜け出せないのではないか?
お墨付きを得るための手段はどこを探したってあるはずがないのに。
お墨付きを得るための手段はどこを探したってあるはずがないのに。
各分野固有の信頼できそうな知識を積み重ねて、再現性がありそうな主張をすることに集中するしかない。
#統計 現実の硬い金属製の精巧なコインで試すと、「表と裏の確率はそれぞれ1/2で、10回のコイン投げは独立」というモデルは極めて適切なモデルであることを確認できます。
サイコロでも同様のことをできる。
それらの場合は、数学的モデルの現実への適用が妥当な場合。
妥当性が不明の場合もある。
サイコロでも同様のことをできる。
それらの場合は、数学的モデルの現実への適用が妥当な場合。
妥当性が不明の場合もある。
https://twitter.com/genkuroki/status/1374972139825078277
#統計 例えば、新型コロナの感染者の推移をあるモデルで予測する場合には、そのモデルの妥当性は大いに疑われるべきでしょう。
現実への統計学の応用ではその手のモデル自体の妥当性が不明な場合の方が多いと思う。
現実への統計学の応用ではその手のモデル自体の妥当性が不明な場合の方が多いと思う。
#統計 関連スレッド
accept, rejectという用語選択は不幸な失敗だった。(統計的検定でお墨付きが得られるという考え方は誤り)
フィッシャーさんとネイマン&ピアソンのピアソンさんによれば、統計的検定は「学習の手段」。
「統計的に有意!」は「ひかえおろう!」という意味ではない(笑)
accept, rejectという用語選択は不幸な失敗だった。(統計的検定でお墨付きが得られるという考え方は誤り)
フィッシャーさんとネイマン&ピアソンのピアソンさんによれば、統計的検定は「学習の手段」。
「統計的に有意!」は「ひかえおろう!」という意味ではない(笑)
https://twitter.com/genkuroki/status/1372910581498318852

#統計 新型コロナ関連の推定や予測という困難な仕事でなくても、モデルの妥当性について考えるべき場合は普通にあります。
例えば共通テストの得点の分布の分析では、統計学入門の教科書によくある「正規分布の仮定」は妥当ではありません。
現役生と浪人生では分布が違う。続く
例えば共通テストの得点の分布の分析では、統計学入門の教科書によくある「正規分布の仮定」は妥当ではありません。
現役生と浪人生では分布が違う。続く
https://twitter.com/genkuroki/status/1374981583388614660
#統計 続き。得点分布を平均と分散の値で代表することは、実質的に正規分布モデルで考えているのと同じです。
現役生と浪人生の特典分布が違っていることが分かっているのですから、単純な正規分布モデルをやめた方が生産的でしょう。
ct.u-tokyo.ac.jp/images/koudai-…


現役生と浪人生の特典分布が違っていることが分かっているのですから、単純な正規分布モデルをやめた方が生産的でしょう。
ct.u-tokyo.ac.jp/images/koudai-…
https://twitter.com/genkuroki/status/1352801024503734273


#統計 高校数学での統計の導入の強引な押し付けを批判するときには、それと同時に「統計学は面白いよ」とにおわせるような話も必要だと思ったので長々と書くことになりました。
批判する側も批判しながら統計学への理解を深めて行くとよいと思いました。
批判する側も批判しながら統計学への理解を深めて行くとよいと思いました。
#統計 中1での確率の話は、某所でのケースでは、教科書本体には掲載されておらず、別の薄い冊子に5ページだけ載っていました。
ペットボトルを投げる話が書いてありますが、全部で5ページなので薄っぺらい内容。
さすがにこれで中1で確率について習ったという扱いは無理。
中2については知らない。
ペットボトルを投げる話が書いてありますが、全部で5ページなので薄っぺらい内容。
さすがにこれで中1で確率について習ったという扱いは無理。
中2については知らない。
https://twitter.com/rochejacmonmo/status/1375030875839074308
• • •
Missing some Tweet in this thread? You can try to
force a refresh