Thread by @JamesWard73

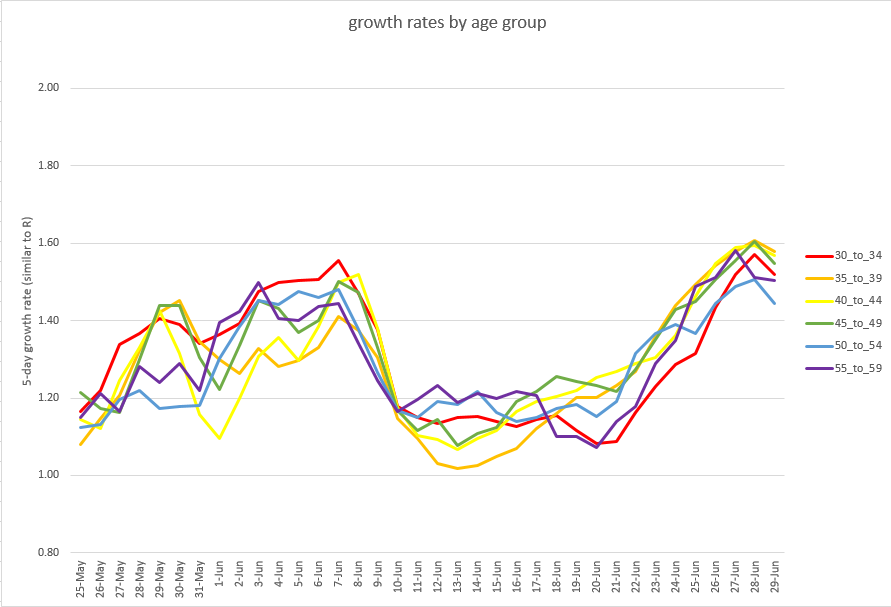
@ThatRyanChap @declamare @whippletom I know you didn’t really ask for this, but I had to go back and check my intuition – and luckily, it’s not wrong. But the exercise was useful because it exposes a couple of interesting dynamics – and helped me understand why we can’t see the impact of delta on hospitalisations.

@ThatRyanChap @declamare @whippletom So here goes: imagine that pre-vaccine we have a population with 1000 cases per day, and 100 hospital admissions per day. So a hospitalisation ratio of 10%. Now let’s suppose that we administer 1 dose of a vaccine that stops 25% of infections, and 80% of hospitalisations

@ThatRyanChap @declamare @whippletom Now we’ll have 750 cases and 20 hospitalisations per day, for a ratio of 2.7%. And let’s apply the second dose, which stops 80% of cases and 95% of hospitalisations. So we’ll have 200 cases and 5 hospitalisations, for a ratio of 2.5%.

@ThatRyanChap @declamare @whippletom So the first part of the intuition was correct: using VE figures similar to the (combined AZ and Pfizer) impact on delta, we get much more benefit in this ratio from the first dose than the second – which reduces cases and hospitalisations roughly in line with each other.

@ThatRyanChap @declamare @whippletom But age-based risk is also important. For simplicity, let’s just deal with two age groups, of equal size. The “old” age group has 500 cases per day, and 90 hospitalisations; while the “young” group also has 500 cases but only 10 hospitalisations. The totals are as before.

@ThatRyanChap @declamare @whippletom Now let’s apply the first doses only to the older group. As you can see in the table, this cuts the overall hospitalisation ratio to 3.2%. If we then apply first doses to the young as well, it comes down a bit further to 2.7%. Second doses in the old then drop it to 1.4%.

@ThatRyanChap @declamare @whippletom And then – interestingly – second doses in the young take it *back up* to 2.5% (because they have a much bigger impact on the overall case total than they do on overall hospitalisations, given that the younger group are at much less risk of going to hospital).

@ThatRyanChap @declamare @whippletom So the second part of the intuition also works: giving doses to the older group is much more powerful in its impact on this ratio, and giving second doses to the old is more impactful than giving first doses to the young.

@ThatRyanChap @declamare @whippletom But of course that’s not quite what happened in reality. We gave out first doses to the elderly when alpha was dominant, so it was alpha’s vaccine efficacy (VE) that governed the impact on this ratio, not delta’s. So let’s try that again, with different VE assumptions:

@ThatRyanChap @declamare @whippletom Now the first step (in red) is giving a first dose to the elderly, assuming 60% VE vs cases rather than 25%. The overall ratio drops to 4% (rather than 3.2% as before). And then the next four steps all happen in quick succession / overlapping with each other:

@ThatRyanChap @declamare @whippletom -Delta arrives, flipping the VE assumption for those who have a first dose
-We give first doses to the young
-And second doses to the elderly
-And delta also increases the risk of hospitalisation by factor of 2

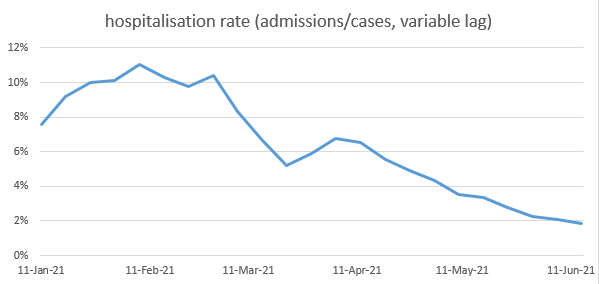
@ThatRyanChap @declamare @whippletom The net effect of these 4 steps is to reduce the ratio from 4% to 2.7% (see the second red column in the table, not quite at the right hand end). So this gives us a clue as to why we find it hard to see the 2x increased risk of delta on hospitalisations in this ratio:

@ThatRyanChap @declamare @whippletom … it came in at the same time as we were getting benefit from first doses in the under-50s, and second doses in the over-50s AND it was also offset to some extent by the impact of delta on VE for those who had had one dose (which increases cases, but not hospitalisations)

@ThatRyanChap @declamare @whippletom Please note this is just a toy model, it doesn’t have a full age structure or precise timing, and the numbers are designed more for ease of explanation than accuracy. But it does I think capture some important dynamics in understanding how this ratio has evolved over time. /end