A powerful idea in math (that nobody teaches you directly…):
If you don't know how to map between two "things," you can often map each of them to the same "canonical thing."
Then you can just go from the 1st thing to the canonical thing, and back to the 2nd thing. [1/n]
If you don't know how to map between two "things," you can often map each of them to the same "canonical thing."
Then you can just go from the 1st thing to the canonical thing, and back to the 2nd thing. [1/n]

This idea shows up all over the place.
I'll give a few examples—but would love to hear about more of them, that show up your neck of the woods.
🌴🌳🌲🐇
[2/n]
I'll give a few examples—but would love to hear about more of them, that show up your neck of the woods.
🌴🌳🌲🐇
[2/n]
One basic question is: how do I express a change of basis between two arbitrary bases (u1,u2) and (v1,v2)?
Answer: the matrix U with columns u1, u2 takes you from the standard basis e1=(1,0), e2=(0,1) to the basis u1,u2. (Just try hitting e1 and e2 with U!)
Then compose…[3/n]
Answer: the matrix U with columns u1, u2 takes you from the standard basis e1=(1,0), e2=(0,1) to the basis u1,u2. (Just try hitting e1 and e2 with U!)
Then compose…[3/n]

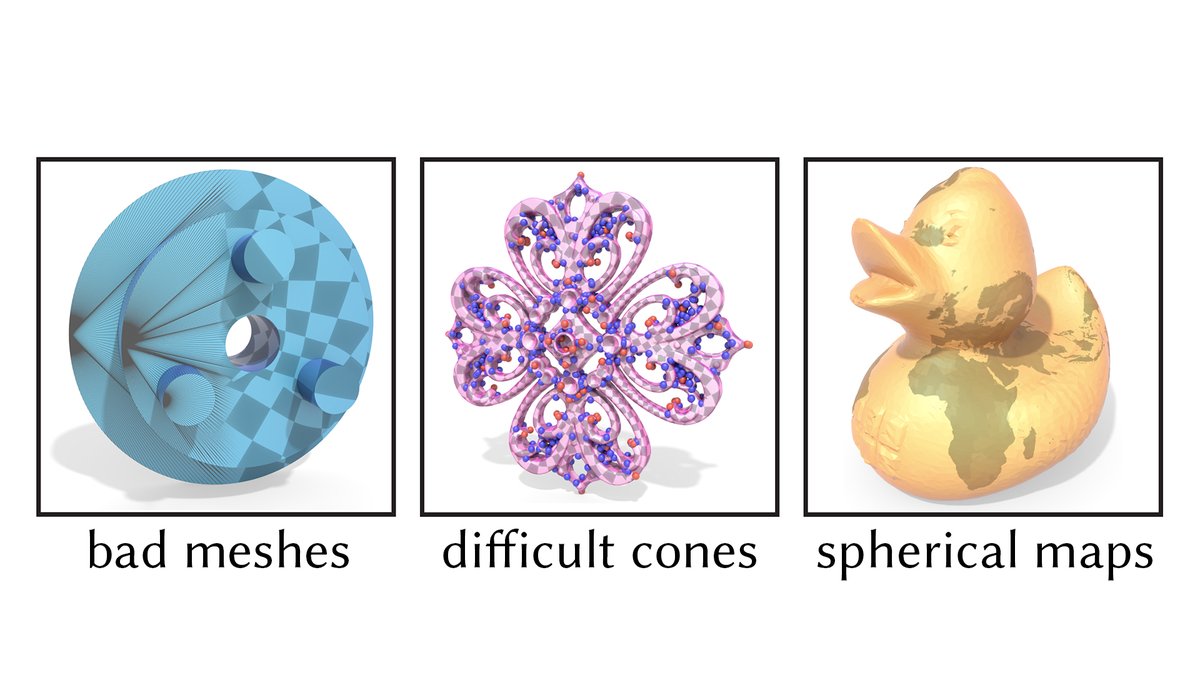
Different question: given two triangulations of the sphere, can I always get from one to the other by flipping edges?
Answer: yes! Pick any triangle abc and flip until c has degree 3. Keep repeating on triangle abx, where x is the remaining neighbor of c.
Then compose… [4/n]
Answer: yes! Pick any triangle abc and flip until c has degree 3. Keep repeating on triangle abx, where x is the remaining neighbor of c.
Then compose… [4/n]

Totally different question: how do I find a nice, bijective map between two smooth surfaces of genus-0?
I won't try to prove this in a tweet, but the answer is: keep smoothing out the curvature until you get a round sphere (Riemann mapping/Yamabe flow).
Then compose… [5/n]
I won't try to prove this in a tweet, but the answer is: keep smoothing out the curvature until you get a round sphere (Riemann mapping/Yamabe flow).
Then compose… [5/n]

What are some other instances of "difficult maps made simple" by first mapping to a canonical object? [n/n]
• • •
Missing some Tweet in this thread? You can try to
force a refresh