
1/
Get a cup of coffee.
In this thread, I'll walk you through the importance of thinking multi-dimensionally.
This is an essential skill for investors. It helps us make better decisions in situations that involve non-linear combinations of several key factors.
Get a cup of coffee.
In this thread, I'll walk you through the importance of thinking multi-dimensionally.
This is an essential skill for investors. It helps us make better decisions in situations that involve non-linear combinations of several key factors.

2/
Recently, I conducted a poll on Twitter.
In the poll, I posed the following question about "chains of kindness" at Starbucks.
(Please read the question, as you'll need it to get through the rest of the thread.)
Recently, I conducted a poll on Twitter.
In the poll, I posed the following question about "chains of kindness" at Starbucks.
(Please read the question, as you'll need it to get through the rest of the thread.)

3/
Answering this question correctly requires non-linear multi-dimensional thinking.
The responses that the poll received suggested that people were having difficulty with this.
That's why I'm writing this thread.
Answering this question correctly requires non-linear multi-dimensional thinking.
The responses that the poll received suggested that people were having difficulty with this.
That's why I'm writing this thread.
4/
Our question has 2 "dimensions" to it.
Dimension 1. The probability that someone *starts* a chain of kindness. In our example, this is 1%.
Dimension 2. The probability that someone *continues* a chain of kindness that they're already a part of. In our example, this is 95%.
Our question has 2 "dimensions" to it.
Dimension 1. The probability that someone *starts* a chain of kindness. In our example, this is 1%.
Dimension 2. The probability that someone *continues* a chain of kindness that they're already a part of. In our example, this is 95%.
5/
Given these 2 dimensions, the question asks what fraction of customers will belong to a chain of kindness.
But here's the problem: the answer depends non-linearly on *both* dimensions.
And our intuition can be unreliable when trying to reason about such situations.
Given these 2 dimensions, the question asks what fraction of customers will belong to a chain of kindness.
But here's the problem: the answer depends non-linearly on *both* dimensions.
And our intuition can be unreliable when trying to reason about such situations.
6/
Our natural instinct leads us to look for "quick shortcuts" when facing such questions.
This is a well-known psychological bias.
Charlie Munger calls this our "Doubt Avoidance Tendency".
From the book Poor Charlie's Almanack:
Our natural instinct leads us to look for "quick shortcuts" when facing such questions.
This is a well-known psychological bias.
Charlie Munger calls this our "Doubt Avoidance Tendency".
From the book Poor Charlie's Almanack:

7/
Doubt Avoidance means we tend to prefer conclusions that can be reached *quickly*.
But *quick* conclusions are not necessarily *correct* ones.
Doubt Avoidance means we tend to prefer conclusions that can be reached *quickly*.
But *quick* conclusions are not necessarily *correct* ones.
8/
For example, the *quickest* way to answer our 2 dimensional question is to focus exclusively on *one* of the two dimensions, neglecting the other one entirely.
That is, some people focus entirely on the 1% number.
Whereas others focus entirely on the 95% number.
For example, the *quickest* way to answer our 2 dimensional question is to focus exclusively on *one* of the two dimensions, neglecting the other one entirely.
That is, some people focus entirely on the 1% number.
Whereas others focus entirely on the 95% number.
9/
The "1 percenters" think like this:
A chain of kindness has a very small probability (1%) of getting started.
So, only a very small fraction of people (< 10%) will end up belonging to a chain.
~38% of poll responders were such "1 percenters".
The "1 percenters" think like this:
A chain of kindness has a very small probability (1%) of getting started.
So, only a very small fraction of people (< 10%) will end up belonging to a chain.
~38% of poll responders were such "1 percenters".
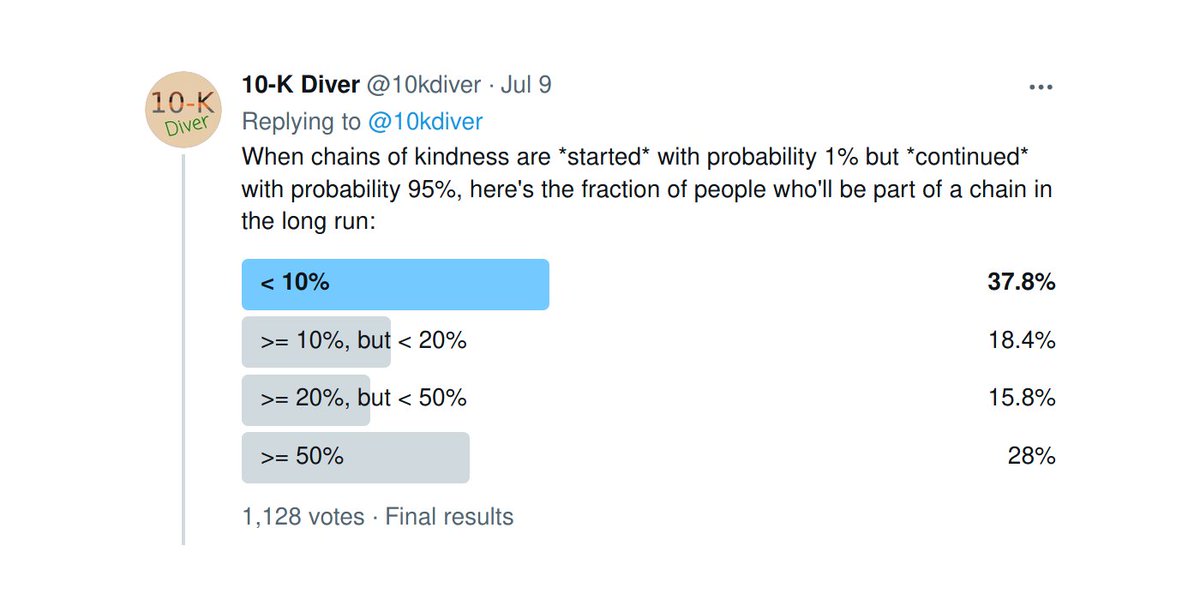
10/
The "95 percenters", on the other hand, think like this:
Sure, a chain may take a while to get started. But once started, it virtually never stops (due to the 95% continuation probability).
So, a large fraction (>= 50%) of customers will end up belonging to a chain.
The "95 percenters", on the other hand, think like this:
Sure, a chain may take a while to get started. But once started, it virtually never stops (due to the 95% continuation probability).
So, a large fraction (>= 50%) of customers will end up belonging to a chain.
11/
From the poll results, it looks like ~28% of responders were "95 percenters".
The upshot was thus a barbell type distribution, where the "1 percenters" and the "95 percenters" together made up ~66% of the population, and voted for the 2 "extreme" answers. No middle ground.
From the poll results, it looks like ~28% of responders were "95 percenters".
The upshot was thus a barbell type distribution, where the "1 percenters" and the "95 percenters" together made up ~66% of the population, and voted for the 2 "extreme" answers. No middle ground.
12/
In this case, *both* the "1 percenters" and the "95 percenters" were wrong.
It's a cardinal mistake to focus exclusively on 1 dimension, when the problem to be solved has 2 (or more) dimensions to it.
In this case, *both* the "1 percenters" and the "95 percenters" were wrong.
It's a cardinal mistake to focus exclusively on 1 dimension, when the problem to be solved has 2 (or more) dimensions to it.
13/
Here's the solution to the problem.
The important thing to note is that *both* dimensions combine together in a non-obvious, non-linear way to determine the final answer.
So, paying attention to just *one* of these dimensions is not a good idea.

Here's the solution to the problem.
The important thing to note is that *both* dimensions combine together in a non-obvious, non-linear way to determine the final answer.
So, paying attention to just *one* of these dimensions is not a good idea.


14/
But it looks like ~66% of the population did just that.
Their sole focus on one dimension blinded them to the importance of the other dimension.
In a world where such uni-dimensional thinking is the norm, a multi-dimensional thinker is likely to possess a definite edge.
But it looks like ~66% of the population did just that.
Their sole focus on one dimension blinded them to the importance of the other dimension.
In a world where such uni-dimensional thinking is the norm, a multi-dimensional thinker is likely to possess a definite edge.
15/
Generalizing this example a bit, we see that analyzing a situation multi-dimensionally is a 3-step process.
Step 1. Identify the key dimensions,
Step 2. Build a multi-dimensional model, and
Step 3. Analyze the model to form a reasonably accurate conclusion.
Generalizing this example a bit, we see that analyzing a situation multi-dimensionally is a 3-step process.
Step 1. Identify the key dimensions,
Step 2. Build a multi-dimensional model, and
Step 3. Analyze the model to form a reasonably accurate conclusion.
16/
Step 1. Identify the key dimensions.
In our problem, the 2 key dimensions were simply given to us.
But in the real world, it's up to us to assess the situation critically and work out what the key dimensions (ie, the most important factors at play) are.
Step 1. Identify the key dimensions.
In our problem, the 2 key dimensions were simply given to us.
But in the real world, it's up to us to assess the situation critically and work out what the key dimensions (ie, the most important factors at play) are.
17/
For example, when deciding whether to invest in a company, it's up to us to identify the key factors likely to shape the company's future.
For Starbucks, this might be their continued expansion into China.
For Amazon, it might be the future of AWS and 3'rd party retailing.
For example, when deciding whether to invest in a company, it's up to us to identify the key factors likely to shape the company's future.
For Starbucks, this might be their continued expansion into China.
For Amazon, it might be the future of AWS and 3'rd party retailing.
18/
Step 2. Build a multi-dimensional model.
For example, we built a Markov Chain that captured all the key aspects of our problem.
Developing fluency with a variety of such mental models is key. More models = more tools we have to accurately reflect our situation.
Step 2. Build a multi-dimensional model.
For example, we built a Markov Chain that captured all the key aspects of our problem.
Developing fluency with a variety of such mental models is key. More models = more tools we have to accurately reflect our situation.
19/
As Charlie Munger says, his "latticework of mental models", consciously honed over many years, is of immense help to him in assessing all kinds of real world situations.
For more on the specific kind of model (ie, Markov Chains) that we used above:
As Charlie Munger says, his "latticework of mental models", consciously honed over many years, is of immense help to him in assessing all kinds of real world situations.
For more on the specific kind of model (ie, Markov Chains) that we used above:
https://twitter.com/10kdiver/status/1383471136868995079
20/
Step 3. Analyze the model to form a reasonably accurate conclusion.
In our example, we used the basic concepts of probability to analyze our Markov Chain model.
Here's a more complete analysis -- a color plot of our "in-chain" fraction of customers versus our 2 dimensions:
Step 3. Analyze the model to form a reasonably accurate conclusion.
In our example, we used the basic concepts of probability to analyze our Markov Chain model.
Here's a more complete analysis -- a color plot of our "in-chain" fraction of customers versus our 2 dimensions:

21/
Here too, it helps to develop familiarity with a variety of analyses.
In business and investing, our "analysis toolbox" should probably include DCFs, Reverse DCFs, Monte-Carlo methods, unit economics and LTV vs CAC analyses, etc.
Here too, it helps to develop familiarity with a variety of analyses.
In business and investing, our "analysis toolbox" should probably include DCFs, Reverse DCFs, Monte-Carlo methods, unit economics and LTV vs CAC analyses, etc.
22/
Another example: Investors tend to focus too much on margins and too little on inventory turns.
But thinking multi-dimensionally about *both* these factors can help us understand the underlying business and its return on capital *much* better.
Another example: Investors tend to focus too much on margins and too little on inventory turns.
But thinking multi-dimensionally about *both* these factors can help us understand the underlying business and its return on capital *much* better.
https://twitter.com/10kdiver/status/1304814783045099520
23/
Peter Lynch's "PEG Ratio" (a company's P/E ratio divided by its annual percentage growth rate) also embodies multi-dimensional thinking.
It's not perfect.
But it usefully balances 2 dimensions (value and growth) via one metric, to screen for "growth at a reasonable price".
Peter Lynch's "PEG Ratio" (a company's P/E ratio divided by its annual percentage growth rate) also embodies multi-dimensional thinking.
It's not perfect.
But it usefully balances 2 dimensions (value and growth) via one metric, to screen for "growth at a reasonable price".
24/
In tech, Steve Jobs clearly understood the importance of multi-dimensional thinking early on.
For example, instead of maximizing the uni-dimensional objective "performance", he steered focus to the multi-dimensional objective *performance per Watt of power consumed*.
In tech, Steve Jobs clearly understood the importance of multi-dimensional thinking early on.
For example, instead of maximizing the uni-dimensional objective "performance", he steered focus to the multi-dimensional objective *performance per Watt of power consumed*.
25/
This multi-dimensional focus drove Apple to pivot from PowerPC to Intel chips, and now from Intel to Apple's own silicon:

This multi-dimensional focus drove Apple to pivot from PowerPC to Intel chips, and now from Intel to Apple's own silicon:


26/
As a final example, here's a video of Charlie Munger explaining how he once used multi-dimensional thinking to help out his friend -- to the tune of hundreds of thousands of dollars!
As a final example, here's a video of Charlie Munger explaining how he once used multi-dimensional thinking to help out his friend -- to the tune of hundreds of thousands of dollars!
27/
Thinking multi-dimensionally is pretty basic. When there are several factors at play, they should all be correctly accounted for.
So basic, yet so often overlooked.
I hope this thread helped inform your thinking on this.
Thank you very much. Enjoy your weekend!
/End
Thinking multi-dimensionally is pretty basic. When there are several factors at play, they should all be correctly accounted for.
So basic, yet so often overlooked.
I hope this thread helped inform your thinking on this.
Thank you very much. Enjoy your weekend!
/End
Several people would like to know the source of the Charlie Munger video above.
It’s a clip from this longer YouTube video.
The whole video (~1 hr, 12 min) is great if you have the time for it. Enjoy!
It’s a clip from this longer YouTube video.
The whole video (~1 hr, 12 min) is great if you have the time for it. Enjoy!
• • •
Missing some Tweet in this thread? You can try to
force a refresh











