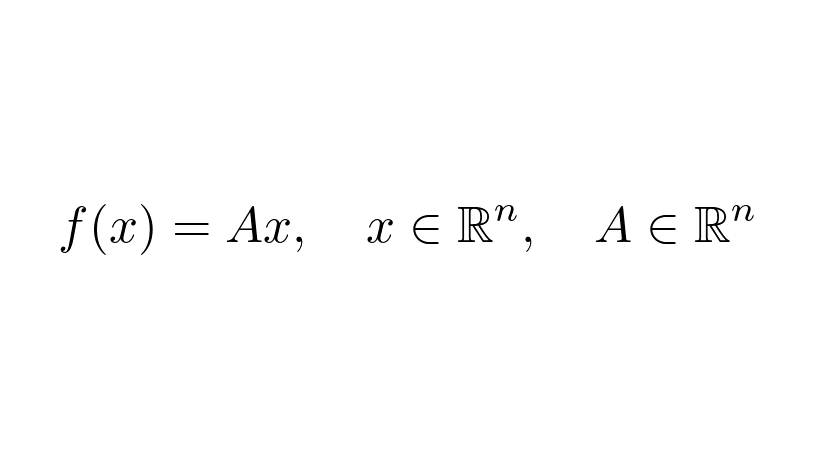Thread by @TivadarDanka

How to build a good understanding of math for machine learning?

I get this question a lot, so I decided to make a complete roadmap for you. In essence, three fields make this up: calculus, linear algebra, and probability theory.

Let's take a quick look at them!

🧵 👇

1. Linear algebra.

In machine learning, data is represented by vectors. Essentially, training a learning algorithm is finding more descriptive representations of data through a series of transformations.

Linear algebra is the study of vector spaces and their transformations.

Simply speaking, a neural network is just a function mapping the data to a high-level representation.

Linear transformations are the fundamental building blocks of these. Developing a good understanding of them will go a long way, as they are everywhere in machine learning.

My favorite learning resources:

• Linear algebra university lectures by Gilbert Strang, taught at MIT (youtube.com/playlist?list=…)

• Linear Algebra Done Right by Sheldon Axler (linear.axler.net)

2. Calculus.

While linear algebra shows how to describe predictive models, calculus has the tools to fit them to the data.

If you train a neural network, you are almost certainly using gradient descent, which is rooted in calculus and the study of differentiation.

Besides differentiation, its "inverse" is also a central part of calculus: integration.

Integrals are used to express essential quantities such as expected value, entropy, mean squared error, and many more. They provide the foundations for probability and statistics.

When doing machine learning, we are dealing with functions with millions of variables.

In higher dimensions, things work differently. This is where multivariable calculus comes in, where differentiation and integration are adapted to these spaces.

My favorite learning resources:

• Single Variable Calculus at MIT (youtube.com/playlist?list=…)

• Khan Academy on Multivariable Calculus (youtube.com/playlist?list=…)

• Multivariable Calculus at MIT (youtube.com/playlist?list=…)

3. Probability theory

How to draw conclusions from experiments and observations? How to describe and discover patterns in them?

These are answered by probability theory and statistics, the logic of scientific thinking.

My favorite learning resources:

• Pattern Recognition and Machine Learning by Christopher Bishop (springer.com/gp/book/978038…)

• The Elements of Statistical Learning by Trevor Hastie, Robert Tibshirani, and Jerome Friedman (web.stanford.edu/~hastie/ElemSt…)

These fields form the foundations of mathematics in machine learning.

This is just the starting point. The most exciting stuff comes after these milestones! Advanced statistics, optimization techniques, backpropagation, the internals of neural networks.

So, how much math do you need to work in machine learning?

You can get started with high school math and pick everything up as you go. Advanced math is NOT a prerequisite.

Here is a recent thread about this by @svpino that sums up my thoughts.

https://twitter.com/svpino/status/1425744306552377347

If you would like to dig deeper, I have two recommendations for you.

First, I have written a long and detailed post, where I talk about each topic and subtopic in detail. This is a guide for your studies.

Check it out!

tivadardanka.com/blog/roadmap-o…

Second, I am writing a complete book about this, where I explain every concept as clearly and intuitively as possible.

The early access program will launch in September, releasing the chapters as I write them.

This is where you can join: tivadar.gumroad.com/l/mathematics-…

My goal is to bring the theory and math behind machine learning closer to everyone while eliminating all gatekeeping.

If you would like to join me on this journey, consider giving me a follow and retweeting the first tweet of this thread!

https://twitter.com/TivadarDanka/status/1426158532311896067