
Thread on deriving India VIX!
Get your pen and paper ready!
The NSE India VIX white paper (link below) only gives the formula and we will derive it in this thread. That'll be the only focus of this thread with more in future threads.
www1.nseindia.com/content/indice…
Get your pen and paper ready!
The NSE India VIX white paper (link below) only gives the formula and we will derive it in this thread. That'll be the only focus of this thread with more in future threads.
www1.nseindia.com/content/indice…
This is going to be mathematical and my post yesterday about expectation and integration should help. But I’ll try to reduce jargon and leave out unnecessary mathematical details. Some topics such as stochastic processes have been touched upon here. Will post more on that later
+
+
Let’s say f(x) is any function of a stock (or any other tradable underlying) ‘x’ and whose 1st & 2nd derivatives exist. Following on from the derivation last time of the PDF of any underlying,
‘x’ has a PDF, φ(k), given in fig below.

‘x’ has a PDF, φ(k), given in fig below.
https://twitter.com/muskk/status/1417803658738114570?ref_src=twsrc%5Etfw
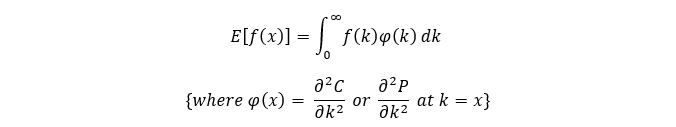
Replacing φ(x) and splitting the integral into two with the x-axis split at forward “F”. We use (OTM) puts for the integral below F and (OTM) calls for integral above F. We proceed as follows (you can ignore the below if not interested in details): 



Hence, we have our most important result in the pic below.
This is called "static replication" of the valuation of the european payoff f(x).
This is called "static replication" of the valuation of the european payoff f(x).

Based on this any twice-differentiable European payoff can be priced using OTM calls and puts with weights (f^'' (k)) determined by the form of the payoff.
This result holds not only for stocks but also fixed-income instruments and those from other asset classes.
This result holds not only for stocks but also fixed-income instruments and those from other asset classes.
This result holds not only for stocks but also fixed-income instruments and those from other asset classes. Let’s look at a few examples quickly.
YOU CAN SKIP THIS SECTION IF FOCUS IS ONLY ON VIX
+

YOU CAN SKIP THIS SECTION IF FOCUS IS ONLY ON VIX
+


Now let’s look, very briefly at the (stochastic) process for the underlying (I’ll cover stochastic processes, without being boring, in a separate thread but for now just focus on the bottom line!)
+
+

Hence we have our VIX below! Finally! (This has been painful… writing all the above in Word Equation editor!)
+
+

Remember above derivation is model independent i.e. no assumptions made on distribution of underlying.
Next, we will try to use the above formula to get some actual values of VIX and look at it’s connection with expected fwd realized variance i.e. Variance swaps!
(END)
Next, we will try to use the above formula to get some actual values of VIX and look at it’s connection with expected fwd realized variance i.e. Variance swaps!
(END)
• • •
Missing some Tweet in this thread? You can try to
force a refresh












