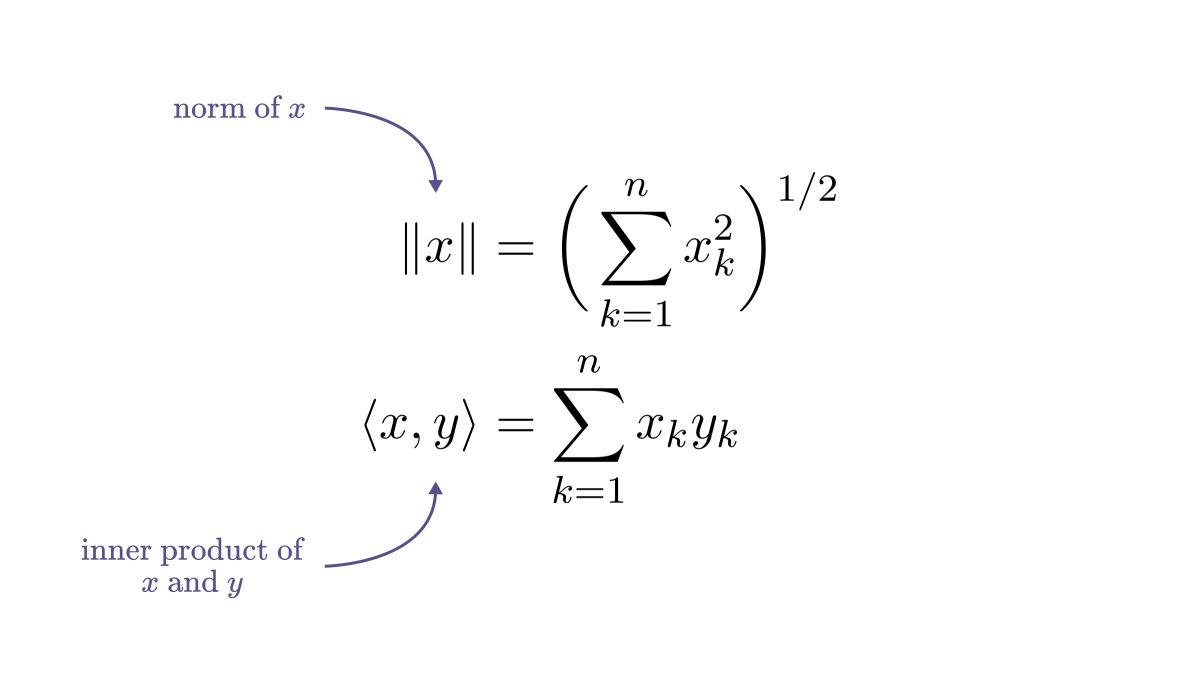
The early access of my Mathematics of Machine Learning book is launching today!
One chapter per week, we go from basics to the internals of neural networks. We are starting with vector spaces, the scene where machine learning happens.
Here is why they are so important!
🧵 👇🏽
One chapter per week, we go from basics to the internals of neural networks. We are starting with vector spaces, the scene where machine learning happens.
Here is why they are so important!
🧵 👇🏽
As you probably know, data is represented by vectors.
Data points are just tuples of measurements. In their raw form, they are hardly useful for us. They are just blips in space.
Data points are just tuples of measurements. In their raw form, they are hardly useful for us. They are just blips in space.

Without operations and transformations, it is difficult to predict class labels or do anything else.
Vector spaces provide a mathematical structure where operations naturally arise.
Instead of a blip, just imagine an arrow pointing to the data point from a fixed origin.
Vector spaces provide a mathematical structure where operations naturally arise.
Instead of a blip, just imagine an arrow pointing to the data point from a fixed origin.

On vectors, we can easily define operations using our geometric intuition.
Addition is translation, while scalar multiplication is scaling.
Addition is translation, while scalar multiplication is scaling.
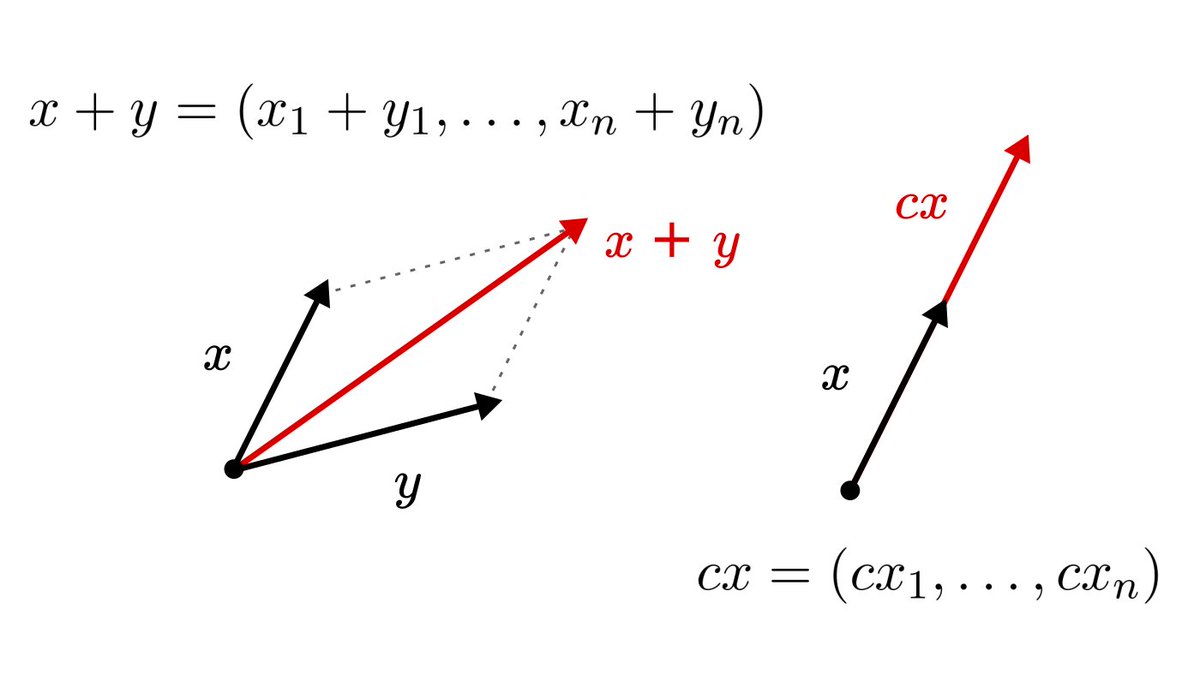
Why do we even need to add data points together?
To transform raw data into a form that can be used for predictive purposes. Raw data can have a really complicated structure, and we aim to simplify it as much as possible.
To transform raw data into a form that can be used for predictive purposes. Raw data can have a really complicated structure, and we aim to simplify it as much as possible.
For instance, raw data is often standardized by subtracting the mean of features and scaling with their variance.
This way, each feature is of the same magnitude, making sure that none of them are dominated by the ones on the largest scale.
This way, each feature is of the same magnitude, making sure that none of them are dominated by the ones on the largest scale.

Aside from the operations, vector spaces give rise to linear transformations.
They are essentially distortions of the vectors space, yielding a new set of features for our dataset.
They are essentially distortions of the vectors space, yielding a new set of features for our dataset.

Despite their simplicity, linear transformations are the main building blocks of most machine learning algorithms.
A neural network is a chain of linear transformations and activation functions, while the famous PCA is a linear transformation itself.
A neural network is a chain of linear transformations and activation functions, while the famous PCA is a linear transformation itself.
The reasoning is simple.
To understand machine learning algorithms, you need to understand linear transformations.
To understand linear transformations, you need to understand vector spaces.
To understand machine learning algorithms, you need to understand linear transformations.
To understand linear transformations, you need to understand vector spaces.
If you are interested in more, I have two resources for you!
First, I recently wrote a post where I explain this idea in detail. You can find it at the link below.
tivadardanka.com/blog/linear-al…
First, I recently wrote a post where I explain this idea in detail. You can find it at the link below.
tivadardanka.com/blog/linear-al…
Second, vector spaces are where my book starts. The early access just launched today with the first chapter. Every week, you'll receive a chapter as I write them.
Check it out and join the journey!
tivadar.gumroad.com/l/mathematics-…
Check it out and join the journey!
tivadar.gumroad.com/l/mathematics-…
• • •
Missing some Tweet in this thread? You can try to
force a refresh