Thread by @svpino

If you want to become a better gambler, you need to learn probabilities.

(Also useful for machine learning, but who cares about that.)

Let's talk about the basic principles of probabilities that you need to understand.

This is what we are going to cover:

The four fundamental rules of probabilities and a couple of basic concepts.

These will help you look at the world in a completely different way.

(And become a better gambler, if that's what you choose to do.)

Let's start with an example:

If you throw a die, you'll get six possible elementary outcomes.

We call the collection of possible outcomes "Sample Space."

The attached image shows the sample space of throwing a single die.

What are the possible elementary outcomes of tossing a coin?

1. We get heads
2. We get tails

Therefore, the sample space of tossing a coin is {Heads, Tails}.

Alright. We have the basic concepts almost out of the way.

Let's see one more example before we move on.

The sample space of throwing a pair of dice has 36 outcomes, as shown in the attached picture.

I made one die white and the other one green. This will help later.

Now we know what "sample space" and "elementary outcomes" are.

Next stop, what's the likelihood of each specific outcome occurring?

If we toss a coin, what's the likelihood of getting heads?

Assuming a fair coin, we should get heads half the time.

In the coin example, we can say that the probability of each outcome looks like this:

1. Getting heads → 0.5
2. Getting tails → 0.5

(Notice how we usually use values between 0 and 1 to define probabilities.)

If we are throwing a single die, the probability of getting any of the numbers is 1/6.

Remember, the sample space of outcomes contains 6 possibilities, one for each side of the die.

Therefore, the probability of getting any of those is 1/6.

If we are throwing a pair of dice, the probability of getting any of the outcomes is 1/36.

For example, getting the white dice to show 4 and the green dice to show 3 is one out of the 36 possible outcomes.

Therefore, the probability of getting that combination is 1/36.

To make things easier to describe, let's introduce the concept of an "event."

An event is a set of outcomes.

We can combine these outcomes using logical operations: AND, OR, and NOT.

For example:

• A: Rolling a 1 when throwing a die.

P(A) = 1/6

Assuming B, C, D, E, and F represent the events of rolling a 2, 3, 4, 5, and 6, respectively, we can easily see that:

P(A)+P(B)+P(C)+P(D)+P(E)+P(F)=1

This is important:

The sum of the probability of all possible outcomes of a sample space is always equal to 1.

If we toss a coin: P(H) + P(T) = 1.

Let's use what we just learned to define the first rule.

Subtraction Rule:

P(A) = 1 - P(not A)

In English: "The probability of an event A happening is the same as 1 minus the probability of the event A not happening."

The Subtraction Rule is helpful when P(not A) is simpler to compute than P(A).

Example: What's the probability of not rolling double 2's with a pair of dice.

• A: Not rolling 2 and 2.
• not A: rolling 2 and 2.

P(A) = 1 - P(not A) = 1 - 1/36 = 35/36.

Let's make things more exciting.

What's the probability of getting the white die show 2 or the green die show 2?

We can manually compute the probability by counting the outcomes of each event.

The answer: 11 out of 36 possible outcomes.

But we can define this more formally with the Addition Rule:

• P(A or B) = P(A) + P(B) - P(A and B)

Let's try to make sense out of this step by step.

Remember:

• A: White dice shows 2.
• B: White dice shows 2.

P(A) = 6/36
P(B) = 6/36

So far, so good but notice something important: There's one outcome that's part of both A and B.

The duplicate outcome is right at the intersection of A and B.

The probability of getting that outcome is P(A and B), and that's the last term of the Addition Rule.

Putting everything together:

P(A or B) = P(A) + P(B) - P(A and B)
P(A or B) = 6/36 + 6/36 - 1/36 = 11/36

In this example, A and B were non-mutually exclusive events.

Here is another example:

• A: Dice add up to 2
• B: Dice add up to 12.

Look at the attached picture and realize these two events don't overlap. Therefore: P(A and B) = 0.

To make sure we are on the same page, here is an exercise to check the Addition Rule:

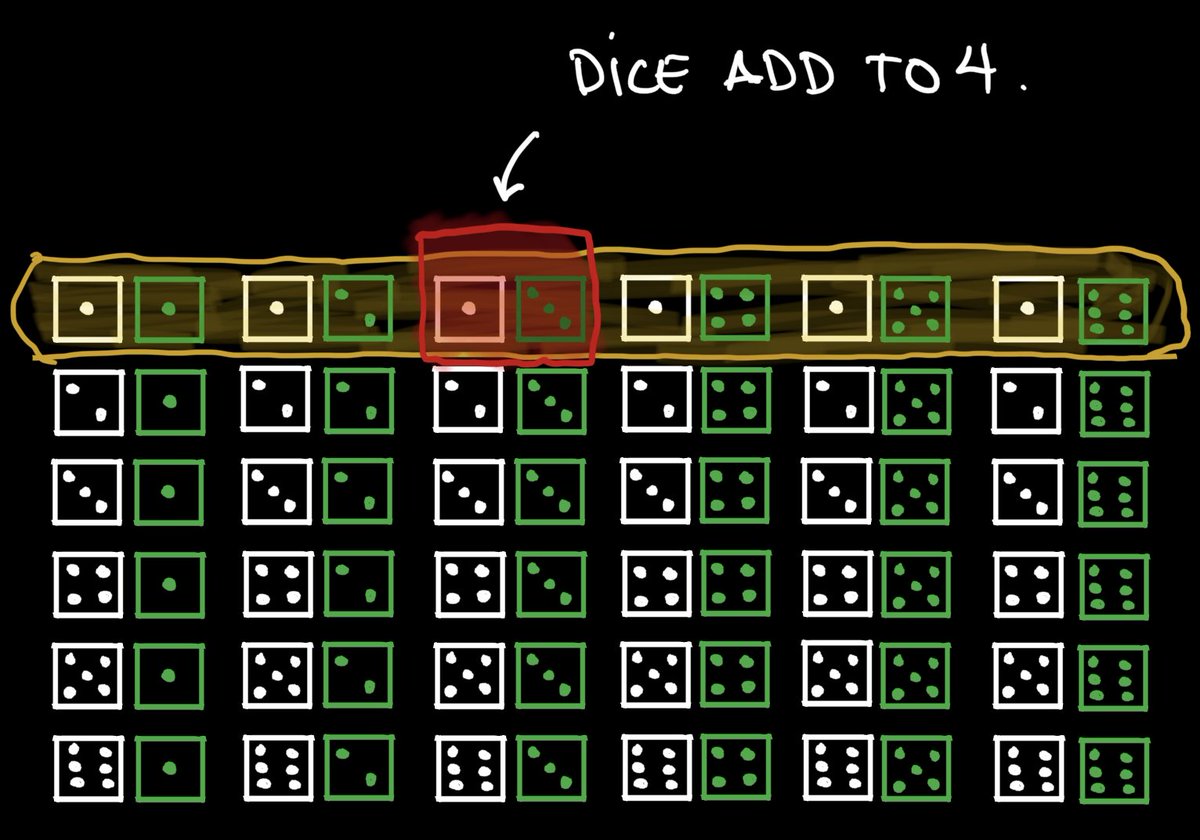
What's the probability of two dice adding up to 4?

We have three possible events:

• A: White shows 3, Green shows 1.
• B: White shows 2, Green shows 2.
• C: White shows 1, Green shows 3.

A, B, and C are mutually exclusive events, so P(A and B and C) = 0.

Assuming X represents the "dice add up to 4" event, we can say:

P(X) = P(A or B or C)

In English: "The probability of the dice adding up to 4 is equal to the probability of getting A or B or C."

Using the Addition Rule:

P(A or B or C) = P(A)+P(B)+P(C)-P(A and B and C)

Let's solve this:

P(X) = 1/36 + 1/36 + 1/36 - 0 = 3/36.

It all works!

There's only one more thing we need to define.

We looked at P(A and B) when A and B are mutually exclusive events.

But how can we solve P(A and B) when A and B aren't mutually exclusive?

Let's talk about Conditional Probabilities.

We already computed the probability of the two dice adding up to 4: 3/36. That's the probability before we throw the dice.

But now, imagine that we throw the white die first and get a 1.

What's the probability now of getting both dice to add up to 4?

Let's break our problem into a couple of events:

• A: Dice add up to 4.
• B: White dice shows 1.

The conditional probability is represented as P(A|B).

In English: "The probability of throwing 2 dice that add up to 4 given that the white dice shows 1."

Event B reduces the sample space from 36 possible outcomes (no dice has been thrown) down to 6 possible outcomes (white dice shows 1.)

Out of those 6 possible outcomes, only one of them gives us the dice adding up to 4.

P(A|B) = 1/6.

See the attached pictures.

Based on this, we can formalize the definition of Conditional Probability:

P(A|B) = P(A and B) / P(B)

Let's make sure everything works:

• P(A and B): Probability of dice adding up to 4 and white dice showing 1 = 1.

• P(B): Probability of white dice showing 1 = 6.

Remember that we wanted to define P(A and B)? We can rearrange the above definition and get the Multiplication Rule:

P(A and B) = P(A|B) * P(B)

But there's one more thing.

A and B are independent events if the occurrence of B doesn't influence the probability of the A.

Therefore, if A and B are independent: P(A|B) = P(A)

We can use this to get a Special Multiplication Rule (when A and B are independent):

P(A and B) = P(A) * P(B)

Let's look at one example:

• A: White dice shows 2.
• B: Green dice shows 3.

Using the Multiplication Rule:

P(A|B) = P(A and B) / P(B)
P(A|B) = 1/36 / 1/6
P(A|B) = 1/6

But since A and B are independent, P(A|B) = P(A), which is clearly true since P(A) = 1/6.

Let's recap.

There are 4 different rules:

1. Addition:
P(A or B) = P(A) + P(B) - P(A and B)

2. Subtraction:
P(A) = 1 - P(not A)

3. Multiplication:
P(A and B) = P(A|B) * P(B)

4. Multiplication when A and B are independent:
P(A and B) = P(A) * P(B)

In addition to that, we defined the following basic concepts:

• Elementary outcomes
• Sample spaces
• Events

These are the fundamental building blocks of probabilities.

Now, you can go and gamble your money away with the confidence of a scientist!

Every week, I post 2 or 3 threads like this, breaking down concepts and giving you ideas on applying them in real-life situations.

You can find more of these at @svpino.

Stay tuned!

Here is a great clarification:

https://twitter.com/mathsppblog/status/1435175124664258561