Thread by @genkuroki

東京大学出版会の『統計学入門』を運悪く「真面目」に読んでしまい、それに従って、「確率ではなく、割合だ」というスタイルで「信頼区間警察」をやっている側が狼藉之義也の「ヒャッハー」達だという問題。

へたをするとこれが高校数学にも伝搬する恐れがある。

https://twitter.com/389jan/status/1436709576603099136

最近の例では

tjo.hatenablog.com/entry/2021/07/…
渋谷駅前で働くデータサイエンティストのブログ
2021-07-16
95%信頼区間の「95%」の意味

がひどい。

教科書に書いてあるという事実は正しいことの証拠にはなりません。

#統計 正しい考え方

* 信頼区間の計算では通常パラメータを持つモデル(例えば正規分布モデルや二項分布モデルなど)が使われる。

* 95%信頼区間の95%はそのモデル内での標本分布で測った確率(の近似値)になる。

* 使用したモデルが現実において妥当でなければ、信頼区間は信頼できないものになる。

確率という言葉を使うことを大学の学部で講義する人の多くは、「どの確率分布(確率測度)で測った確率であるか」を明確にしておかないと危ないことについても話すと思います。

95%信頼区間の95%についても同じことが当てはまります。その95%はモデル内標本分布で測った確率(の近似値)になる。

どの確率測度で測ったものであるかを明瞭に理解していれば、「確率」と呼んでも全然問題ないことは自明です。これがアウトなら、「確率」という用語を使える場面がなくなってしまいます(笑)。

それなのに「確率ではなく、割合だ」と狼藉之義也なことを言う人達がいる。

一般教養的に、最重要なことは

　信頼区間を計算するために使ったモデルが
　現実において妥当でなければ、
　その信頼区間は信頼できないものになる

だと思います。この事実を認識できていないと、信頼区間を示されただけで、精神的に平伏すしかなくなってしまう危険性がある。

それはまずい。

幅を持たせた予測を目にすることは日常生活で普通にあります。

「幅を持たせた予測」の背後にあるモデルやパラメータを変えれば当然予測も変わります。

その辺の事柄を普通に理解している人たちが増えないと社会的に有害なことが起こりまくり易くなります。そうなることを防ぐ教育が必要です。

「確率ではなく、割合だ！ヒャッハー！」的な狼藉之義也は肝腎の事柄についてひどくミスリーディングなことをやっているので、きちんと「社会的に有害」扱いして行く必要があります。

#統計 使用したモデルが現実において妥当でなければそのモデルを使って得た結果は信頼できないものになる。

こういう当たり前の話は信頼区間についても当然当てはまるのですが、学部生向けの統計学の教科書でその辺がクリアに説明されていないことは、非常に困ったことだと思います。

#統計 学部生向けの統計学の教科書でその辺がクリアに説明されていないことは、学部生向けの統計学の教科書を読んだ人の多くが、「正規分布を仮定しちゃっていいの？」という疑問を解消できなくなっていることからもよく分かります。

#統計 統計学が専門でなくても、統計学の講義をする仕事が割り振られる場合がある。

実際にそうなった人は、学部生向けの統計学の教科書達の内容をチェックすることになるのですが、多くの基本的な疑問が解消しそうもない書き方がされているので、大変な恐怖を感じた人は非常に沢山いると思う。

#統計 しかもその説明が曖昧にされている部分は、

　統計学を使えば科学的にお墨付きが得られる

という

　幻想

を払拭できなくするように曖昧に説明されているのではないかと推測すると辻褄がかなり合う感じ。

#統計 例えば、信頼区間もモデル依存(例えば正規分布モデル依存)であり、モデルが妥当でないと信頼区間も信頼できないものになることを強調してしまうと、信頼区間はそれ単体で科学的なお墨付きが得られる類の道具では決してないことが明瞭になってしまう。

そういうことを避けているのではないか？😱

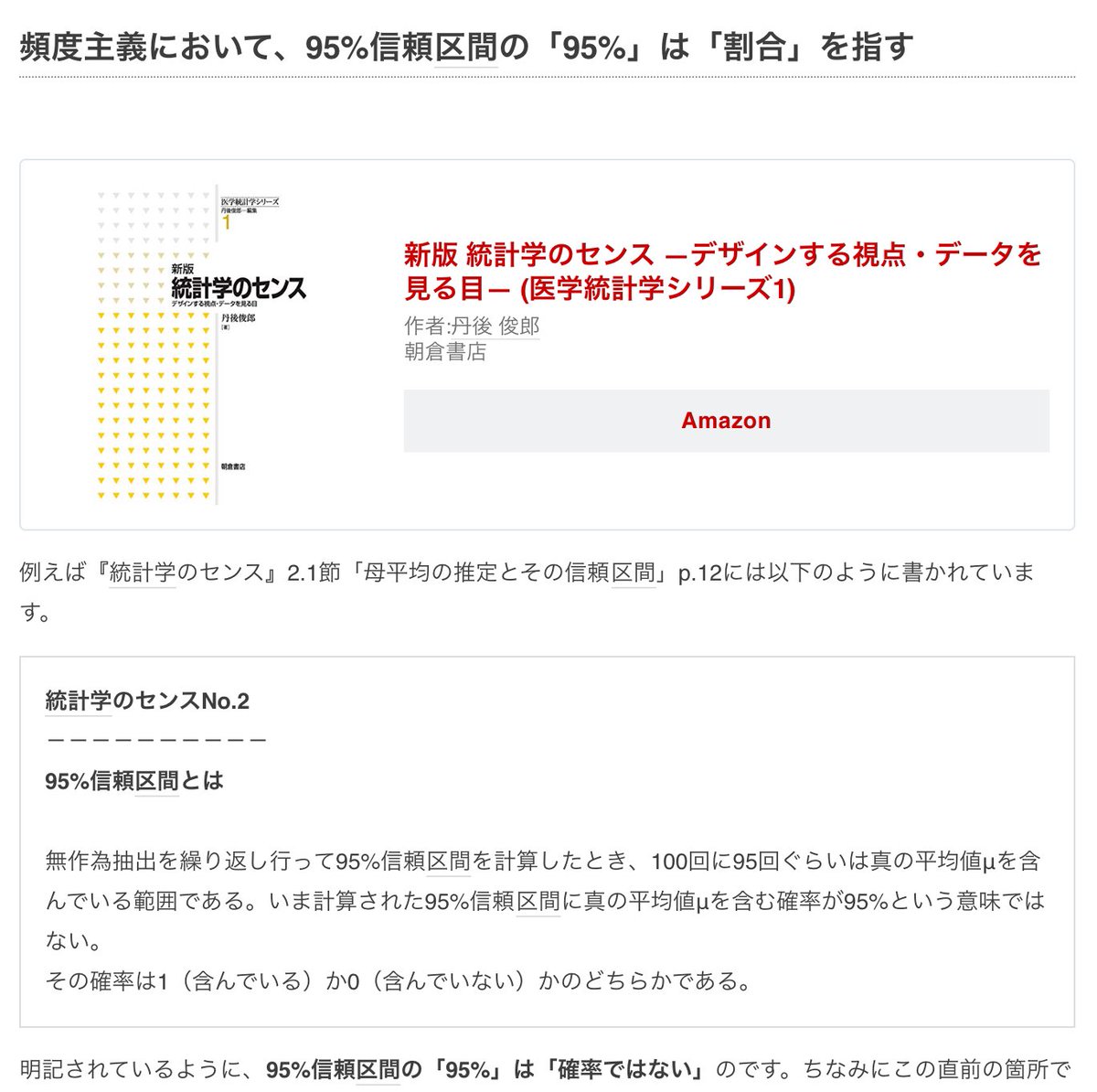
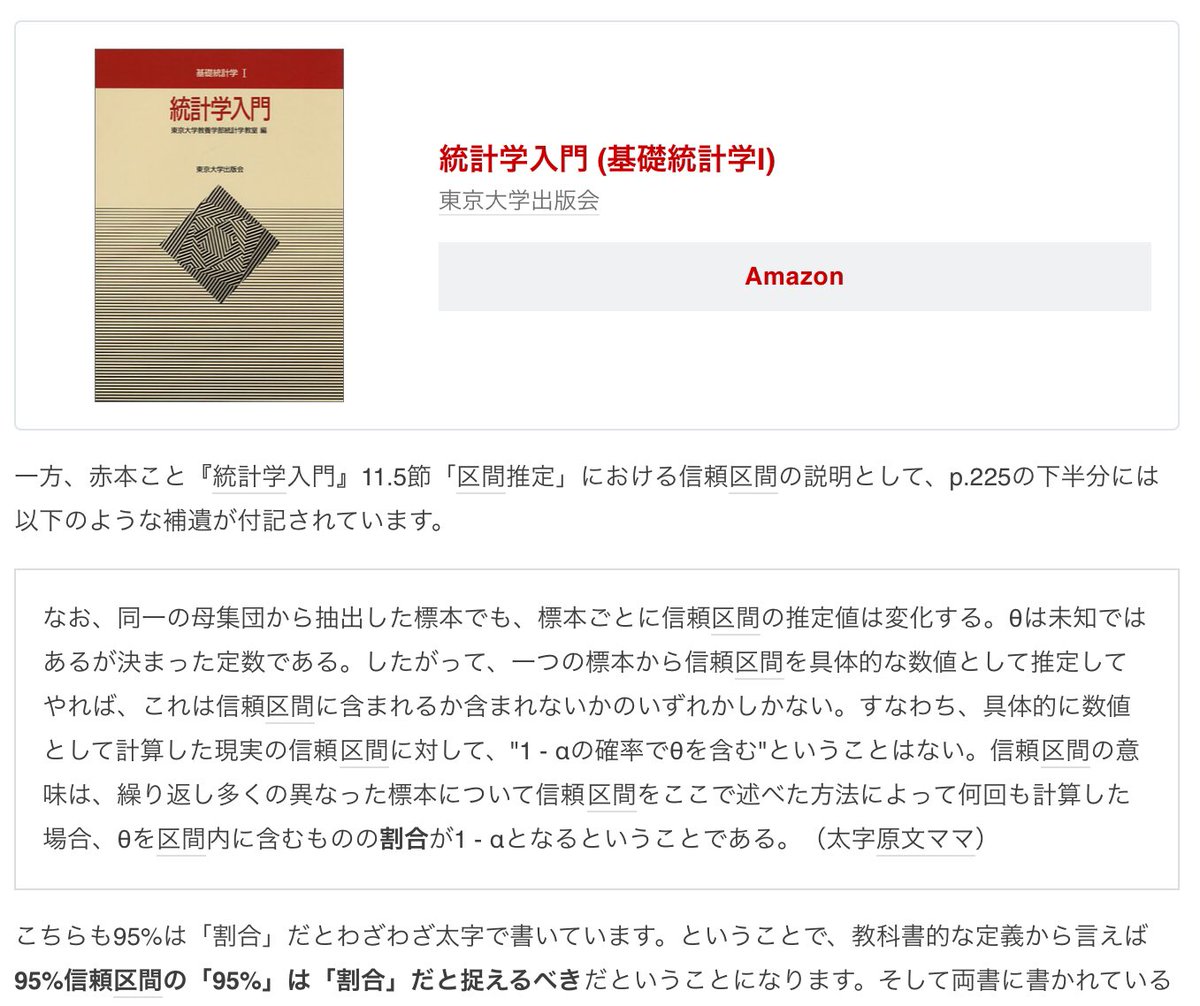
#統計 添付画像中の95%信頼区間の説明において、仮想的に無作為抽出を繰り返す対象は現実の母集団ではなく、信頼区間を計算するために用いた数学的モデル内における仮想的な母集団でなければいけません。

添付画像のような説明の仕方は、現実とモデルの区別を曖昧にする非科学的な説明の仕方です。

#統計 95%信頼区間の95%が数学的なモデル内における割合(注意：測度論的確率論の定式化では確率と割合は同じ意味になる)に過ぎず、「仮に現実で無作為抽出を繰り返したらどうなるか」という意味での割合ではありません。

#統計 「確率ではなく割合だ」などと自明に誤解を招く説明をしながら、現実とモデルの区別を曖昧にするスタイル。

実はこの件について酷いことは他にもあって、ベイズ統計での信用区間についてのデタラメもおまけでついて来ることが多い。

#統計 悪しき「信頼区間警察」達の言説では

❌95%信頼区間の95%は確率ではなく割合だ！

という誤解だけではなく、

❌ベイズ統計における95%信用区間では真の値がそこに含まれる確率は95%であると言ってもよい！

というさらにひどいデタラメを主張する所までがワンセット。

#統計 誰でも馬鹿なことを述べてしまうことがあるので、単に間違っているだけで、大問題だと騒ぐのは間違っています。

しかし、以上の件で、おかしなことを言っている人達が、誤りを素直に認めて謝罪しているのを見たことがない。

おそらく自分達は間違っていないと本心から信じ続けている。😭

#統計 学部生向けの統計学の教科書では、正規分布モデルとt分布を使った平均の信頼区間の計算の仕方が大抵載っています。

母集団が正規分布からずれている実践的に普通の状況での、そのように計算した信頼区間の信頼性に関する詳しい説明については、私のツイログを参照。
↓
twilog.org/genkuroki/sear…

#統計 正規分布モデルとt分布を使った平均の信頼区間では、中心極限定理が効いて来る状況なので、母集団分布が正規分布から少しだけずれている程度なら、95%信頼区間の95%は信頼できる数値になります。

しかしずれが大きいとアウトになります。

詳しくはツイログを参照
↓
twilog.org/genkuroki/sear…

#統計 この辺は、コンピュータで「正規分布モデルを使った95%信頼区間の95%という数値が信頼できなくなる場合の例」を複数作ってみる経験抜きに納得するのは無理だと思います。

私のツイログをあされば #Julia言語 を使ってそのような例を作るコードを丸ごと見ることができます。

#統計 n→∞での漸近論が有効な領域でどうであるかなら、ちょっと数学ができれば、比較的容易に色々わかる。

しかし、nが有限の小さめの値の場合には、実際にコンピュータで計算しないとよく分からないことが多い。

この「小さめの値」が曲者でn=100万でも「小さめの値」とみなすべき場合がある。